
Hemicontinuity
Encyclopedia
In mathematics
, the notion of the continuity
of functions
is not immediately extendible to multi-valued mappings or correspondences
. The dual concepts of upper hemicontinuity and lower hemicontinuity facilitate such an extention. A correspondence that has both properties is said to be continuous in an analogy to the property of the same name for functions.
Upper hemicontinuity is approximately when the graph of the correspondence is closed from the left and from the right (but not necessarily closed at every point). And Lower hemicontinuity is approximately when the graph has no closed edges (i.e. a point that a convergent sequence in the range can reach from the left or right, but not from the other direction).
One should be warned that the term upper semicontinuous, instead of upper hemicontinuous, has been more widespread in the literature. Then upper hemicontinuous is reserved for upper semicontinuity with respect to the weak topology.
The range of Γ : A → B is the set
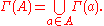
Closed Graph Theorem: For correspondence Γ : A → B with closed values (i.e. Γ (a) - closed for a in A) and compact range, to be upper hemicontinuous it is sufficient and necessary to have closed graph in A×B.
in A×B.
Sequential characterization: Γ : A → B is upper hemicontinuous at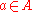 if
if 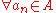 ,
, 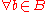 , and
, and 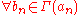
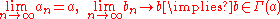
If Γ is compact-valued, the converse is also true.
if for any open set V intersecting Γ(a) there exists neighbourhood U of a such that Γ(x) intersects V for all x in U. (Here V intersects S means nonempty intersection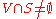 ).
).
One should be warned that the term lower semicontinuous, instead of lower hemicontinuous, has been more widespread in the literature. Then lower hemicontinuous is reserved for lower semicontinuity with respect to the weak topology.
Sequential characterization: Γ : A → B is lower hemicontinuous at a if and only if
 subsequence of
subsequence of 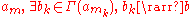
Open Graph Theorem: If Γ : A → B has open graph Gr(Γ), then it is lower hemicontinuous.
usually preserve the type of continuity. But this should be taken with appropriate care since, for example there exists a pair of lower hemicontinuous correspondences whose intersection is not lower hemicontinuous. This can be fixed upon strengthening continuity properties: if one of those lower hemicontinuous multifunctions has open graph then their intersection is again lower hemicontinuous.
Very important part of set-valued analysis (in view of applications) constitutes the investigation of single-valued selections and approximations to multivalued maps. Typically lower hemicontinuous correspondences admit single-valued selections (Michael selection theorem
, Bressan-Colombo directionally continuous selection theorem, Fryszkowski decomposable map selection), likewise upper hemicontinuous maps admit approximations (e.g. Ancel-Granas-Górniewicz-Kryszewski theorem).
(For the notion of hyperspace compare also power set and function space
).
Using lower and upper Hausdorff uniformity
we can also define the so-called upper and lower semicontinuous maps in the sense of Hausdorff (also known as metrically lower / upper semicontinuous maps).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the notion of the continuity
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
of functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
is not immediately extendible to multi-valued mappings or correspondences
Correspondence (mathematics)
In mathematics and mathematical economics, correspondence is a term with several related but not identical meanings.* In general mathematics, correspondence is an alternative term for a relation between two sets...
. The dual concepts of upper hemicontinuity and lower hemicontinuity facilitate such an extention. A correspondence that has both properties is said to be continuous in an analogy to the property of the same name for functions.
Upper hemicontinuity is approximately when the graph of the correspondence is closed from the left and from the right (but not necessarily closed at every point). And Lower hemicontinuity is approximately when the graph has no closed edges (i.e. a point that a convergent sequence in the range can reach from the left or right, but not from the other direction).
Upper hemicontinuity
A correspondence Γ : A → B is said to be upper hemicontinuous at the point a if for any open neighbourhood V of Γ(a) there exists a neighbourhood U of a such that Γ(x) is a subset of V for all x in U.One should be warned that the term upper semicontinuous, instead of upper hemicontinuous, has been more widespread in the literature. Then upper hemicontinuous is reserved for upper semicontinuity with respect to the weak topology.
The range of Γ : A → B is the set
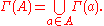
Closed Graph Theorem: For correspondence Γ : A → B with closed values (i.e. Γ (a) - closed for a in A) and compact range, to be upper hemicontinuous it is sufficient and necessary to have closed graph
 in A×B.
in A×B.Sequential characterization: Γ : A → B is upper hemicontinuous at
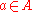 if
if 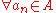 ,
, 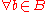 , and
, and 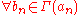
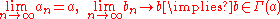
If Γ is compact-valued, the converse is also true.
Lower hemicontinuity
A correspondence Γ : A → B is said to be lower hemicontinuous at the point aif for any open set V intersecting Γ(a) there exists neighbourhood U of a such that Γ(x) intersects V for all x in U. (Here V intersects S means nonempty intersection
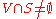 ).
).One should be warned that the term lower semicontinuous, instead of lower hemicontinuous, has been more widespread in the literature. Then lower hemicontinuous is reserved for lower semicontinuity with respect to the weak topology.
Sequential characterization: Γ : A → B is lower hemicontinuous at a if and only if
 subsequence of
subsequence of 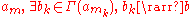
Open Graph Theorem: If Γ : A → B has open graph Gr(Γ), then it is lower hemicontinuous.
Properties
Set-theoretic, algebraic and topological operations on multivalued maps (like union, composition, sum, convex hull, closure)usually preserve the type of continuity. But this should be taken with appropriate care since, for example there exists a pair of lower hemicontinuous correspondences whose intersection is not lower hemicontinuous. This can be fixed upon strengthening continuity properties: if one of those lower hemicontinuous multifunctions has open graph then their intersection is again lower hemicontinuous.
Very important part of set-valued analysis (in view of applications) constitutes the investigation of single-valued selections and approximations to multivalued maps. Typically lower hemicontinuous correspondences admit single-valued selections (Michael selection theorem
Michael selection theorem
In functional analysis, a branch of mathematics, the most popular version of the Michael selection theorem, named after Ernest Michael, states the following:- Other selection theorems :* Zero-dimensional Michael selection theorem...
, Bressan-Colombo directionally continuous selection theorem, Fryszkowski decomposable map selection), likewise upper hemicontinuous maps admit approximations (e.g. Ancel-Granas-Górniewicz-Kryszewski theorem).
Implications for continuity
If a correspondence is both upper hemicontinuous and lower hemicontinuous, it is said to be continuous. A continuous function is in all cases both upper and lower hemicontinuous.Other concepts of continuity
The upper and lower hemicontinuity might be viewed as usual continuity:- Γ : A → B is lower [resp. upper] hemicontinuous if and only if the mapping Γ : A → P(B) is continuous where the hyperspace P(B) has been endowed with the lower [resp. upper] Vietoris topology.
(For the notion of hyperspace compare also power set and function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
).
Using lower and upper Hausdorff uniformity
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
we can also define the so-called upper and lower semicontinuous maps in the sense of Hausdorff (also known as metrically lower / upper semicontinuous maps).

