Choice function
Encyclopedia
A choice function is a mathematical function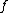 
that is defined on some collection 
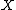of nonempty sets and assigns to each set 
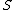in that collection some element 
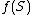of 
. In other words,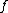 
is a choice function for 
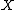if and only if it belongs to the direct product
of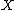
.
(1904) introduced choice functions as well as the axiom of choice (AC) and proved the well-ordering theorem
, which states that every set can be well-ordered. AC states that every set of nonempty sets has a choice function. A weaker form of AC, the axiom of countable choice
(ACω) states that every countable set
of nonempty sets has a choice function. However, in the absence of either AC or ACω, some sets can still be shown to have a choice function.
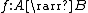is said to be a selection of a multivalued map
φ:A → B ( that is, a function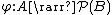
from A to the power set 
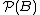), if
The existence of more regular choice functions, namely continuous or measurable selections (see:
) is important in the theory of differential inclusions, optimal control
, and mathematical economics.
that had a
symbol which could be interpreted as choosing a set (if one existed) which satisfies a given proposition. So if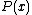 
is a proposition 
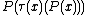was equivalent to 
.
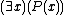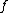that is defined on some collection 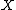of nonempty sets and assigns to each set 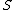in that collection some element 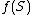of . In other words, 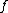is a choice function for 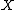if and only if it belongs to the direct productDirect product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
of
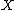.An Example
Let X = { {1,4,7}, {9}, {2,7} }. Then the function that assigns 7 to the set {1,4,7}, 9 to {9}, and 2 to {2,7} is a choice function on X.History and Importance
Ernst ZermeloErnst Zermelo
Ernst Friedrich Ferdinand Zermelo was a German mathematician, whose work has major implications for the foundations of mathematics and hence on philosophy. He is known for his role in developing Zermelo–Fraenkel axiomatic set theory and his proof of the well-ordering theorem.-Life:He graduated...
(1904) introduced choice functions as well as the axiom of choice (AC) and proved the well-ordering theorem
Well-ordering theorem
In mathematics, the well-ordering theorem states that every set can be well-ordered. A set X is well-ordered by a strict total order if every non-empty subset of X has a least element under the ordering. This is also known as Zermelo's theorem and is equivalent to the Axiom of Choice...
, which states that every set can be well-ordered. AC states that every set of nonempty sets has a choice function. A weaker form of AC, the axiom of countable choice
Axiom of countable choice
The axiom of countable choice or axiom of denumerable choice, denoted ACω, is an axiom of set theory, similar to the axiom of choice. It states that any countable collection of non-empty sets must have a choice function...
(ACω) states that every countable set
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
of nonempty sets has a choice function. However, in the absence of either AC or ACω, some sets can still be shown to have a choice function.
- If
is a finite set of nonempty sets, then one can construct a choice function for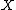 
by picking one element from each member of 
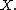This requires only finitely many choices, so neither AC or ACω is needed.
- If every member of
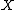is a nonempty set, and the unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
is well-ordered, then one may choose the least element of each member of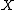 
. In this case, it was possible to simultaneously well-order every member of 
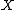by making just one choice of a well-order of the union, so neither AC nor ACω was needed. (This example shows that the well-ordering theorem implies AC. The converse is also true, but less trivial.)
Refinement of the notion of choice function
A function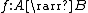 is said to be a selection of a multivalued mapMultivalued function
In mathematics, a multivalued function is a left-total relation; i.e. every input is associated with one or more outputs...
φ:A → B ( that is, a function
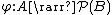from A to the power set 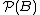), ifThe existence of more regular choice functions, namely continuous or measurable selections (see:
) is important in the theory of differential inclusions, optimal control
Optimal control
Optimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
, and mathematical economics.
Bourbaki tau function
Nicholas Bourbaki used a formalism for set theorySet theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
that had a
symbol which could be interpreted as choosing a set (if one existed) which satisfies a given proposition. So if 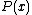is a proposition 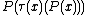was equivalent to .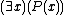