Higher local field
Encyclopedia
In mathematics, a higher (-dimensional) local field is an important example of a complete discrete valuation field. The usual local fields
(typically completions of number fields or the quotient fields
of local ring
s of algebraic curve
s) have associated to them a unique surjective discrete valuation (taking values in the integers), this is by virtue of simply being a complete discrete valuation field and so the same thing holds in higher dimensions. In contrast to the basic local fields, however, higher local fields have a string of residue fields
. and several different candidates for the ring of integers. Geometrically, higher local fields appear via a process of localization
and completion
of local rings of higher dimensional schemes
. Higher local fields are an important part of the subject of higher dimensional number theory, forming the appropriate collection of objects for local considerations.
or 
to have dimension 1), then we say a complete discrete valuation field has dimension n if its residue field has dimension n-1. Higher local fields are those of dimension greater than 1, it is clear that one dimensional local fields are the traditional local fields. We call the residue field of a finite dimensional higher local field the 'first' residue field, it's residue field is then the second residue field, and the pattern continues until we reach a finite field.
over the p-adic numbers: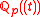
. In fact, these fields can be used in the classification of all two-dimensional local fields of having both characteristic
0 and a residue field (which is just the p-adic numbers in our example) of characteristic 0. This situation can be described as equi-characteristic 0. If we want equi-characteristic p, we similarly use the fields
, Laurent series in two variables over a finite field. There is also the interesting example of mixed characteristic, in which the field itself has characteristic zero, but its (first) residue field has characteristic p. The prototype is denoted 
and is defined as the set of formal sums over the integers, with p-adic coefficients, having infimum valuation with respect to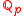 
finite (in which we also exclude infinitely negative) and tending to zero as their index approaches minus infinity.
There is also a construction using commutative algebra, which becomes technical for non-regular rings. The starting point is a Noetherian, regular, n-dimensional ring and a full flag of prime ideals such that their corresponding quotient ring is regular. A series of completions and localisations take place as above until an n-dimensional local field is reached.
, where n is the dimension of the field, which then appears as the domain of a reciprocity map to the Galois group of the maximal abelian extension over the field. This is compatible with local class field theory of the residue field, using the border map of Milnor K-theory to create a commutative diagram involving the reciprocity map on the level of the field and the residue field.
associated to arithmetic schemes (the definition of which involves a product over a full flag for the scheme), there is an adelic formulation of higher global class field theory.
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
(typically completions of number fields or the quotient fields
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
of local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
s of algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
s) have associated to them a unique surjective discrete valuation (taking values in the integers), this is by virtue of simply being a complete discrete valuation field and so the same thing holds in higher dimensions. In contrast to the basic local fields, however, higher local fields have a string of residue fields
Residue field
In mathematics, the residue field is a basic construction in commutative algebra. If R is a commutative ring and m is a maximal ideal, then the residue field is the quotient ring k = R/m, which is a field...
. and several different candidates for the ring of integers. Geometrically, higher local fields appear via a process of localization
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
and completion
Completion (ring theory)
In abstract algebra, a completion is any of several related functors on rings and modules that result in complete topological rings and modules. Completion is similar to localization, and together they are among the most basic tools in analysing commutative rings. Complete commutative rings have...
of local rings of higher dimensional schemes
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
. Higher local fields are an important part of the subject of higher dimensional number theory, forming the appropriate collection of objects for local considerations.
Definition
Any complete discrete valuation field has a (possibly infinite) complete discrete valuation dimension, which can be defined inductively as follows. Finite fields have dimension 0 and complete discrete valuation fields with finite residue field have dimension one (it is natural to also define archimedean local fields such as or to have dimension 1), then we say a complete discrete valuation field has dimension n if its residue field has dimension n-1. Higher local fields are those of dimension greater than 1, it is clear that one dimensional local fields are the traditional local fields. We call the residue field of a finite dimensional higher local field the 'first' residue field, it's residue field is then the second residue field, and the pattern continues until we reach a finite field.Examples
A typical example of a two-dimensional local field is the field of Laurent seriesLaurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
over the p-adic numbers:
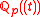. In fact, these fields can be used in the classification of all two-dimensional local fields of having both characteristicCharacteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
0 and a residue field (which is just the p-adic numbers in our example) of characteristic 0. This situation can be described as equi-characteristic 0. If we want equi-characteristic p, we similarly use the fields
, Laurent series in two variables over a finite field. There is also the interesting example of mixed characteristic, in which the field itself has characteristic zero, but its (first) residue field has characteristic p. The prototype is denoted and is defined as the set of formal sums over the integers, with p-adic coefficients, having infimum valuation with respect to 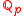finite (in which we also exclude infinitely negative) and tending to zero as their index approaches minus infinity.Constructions
Higher local fields appear in a variety of contexts. A geometric example is as follows. Given a surface over a finite field of characteristic p, a curve on the surface and a point on the curve, take the local ring at the point. Then, complete this ring, localise it at the curve and complete the resulting ring. Finally, take the quotient field. The result is a two-dimensional local field over a finite field.There is also a construction using commutative algebra, which becomes technical for non-regular rings. The starting point is a Noetherian, regular, n-dimensional ring and a full flag of prime ideals such that their corresponding quotient ring is regular. A series of completions and localisations take place as above until an n-dimensional local field is reached.
Topology
One dimensional local fields are usually considered in the valuation topology, in which the discrete valuation is used to define open sets. This will not suffice for higher dimensional local fields, as they usually consist of Laurent series, which don't converge in the valuation topology. Another failure with respect to topology is the fact that there is no ring topology in dimension 2 and above. This, for example, causes an issue in producing the existence theorem for class field theory. It is now known that we can deduce this result in other topologies. There are many open questions in this direction.Class field theory
Local class field theory in dimension one has its analogues in higher dimensions. The appropriate replacement for the multiplicative group becomes the nth Milnor K-groupAlgebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
, where n is the dimension of the field, which then appears as the domain of a reciprocity map to the Galois group of the maximal abelian extension over the field. This is compatible with local class field theory of the residue field, using the border map of Milnor K-theory to create a commutative diagram involving the reciprocity map on the level of the field and the residue field.
Higher adeles
Higher local fields are the components of higher adelesAdele ring
In algebraic number theory and topological algebra, the adele ring is a topological ring which is built on the field of rational numbers . It involves all the completions of the field....
associated to arithmetic schemes (the definition of which involves a product over a full flag for the scheme), there is an adelic formulation of higher global class field theory.