History of variational principles in physics
Encyclopedia
A variational principle in physics is an alternative method for determining the state or dynamics of a physical system, by identifying it as an extremum (minimum, maximum or saddle point) of a function or functional. This article describes the historical development of such principles.
and refraction
of light
. Hero of Alexandria
noted that the law of reflection
follows from the assumption that light travels along the shortest distance between two given points.
by Pierre de Fermat
, who, in the 17th century, refined the principle to "light travels between two given points along the path of shortest time"; now known as the principle of least time or Fermat's principle
.
, who wrote about it in 1744 and 1746, although the true priority is less clear, as discussed below.
Maupertuis felt that "Nature is thrifty in all its actions", and applied the principle broadly: "The laws of movement and of rest deduced from this principle being precisely the same as those observed in nature, we can admire the application of it to all phenomena. The movement of animals, the vegetative growth of plants ... are only its consequences; and the spectacle of the universe becomes so much the grander, so much more beautiful, the worthier of its Author, when one knows that a small number of laws, most wisely established, suffice for all movements."
In application to physics, Maupertuis suggested that the quantity to be minimized was the product of the duration (time) of movement within a system by the "vis viva
", twice what we now call the kinetic energy of the system.
Leonhard Euler
gave a formulation of the action principle in 1744, in very recognizable terms, in the Additamentum 2 to his "Methodus Inveniendi Lineas Curvas Maximi Minive Proprietate Gaudentes". He begins the second paragraph :
A translation of this passage reads:
As Euler states,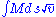
is the integral of the momentum over distance traveled which, in modern notation, equals the reduced action 
. Thus, Euler made an equivalent and (apparently) independent statement of the variational principle in the same year as Maupertuis, albeit slightly later. Curiously, Euler did not claim any priority, as the following episode shows.
Maupertuis' priority was disputed in 1751 by the mathematician Samuel König, who claimed that it had been invented by Gottfried Leibniz
in 1707. Although similar to many of Leibniz's arguments, the principle itself has not been documented in Leibniz's works. König himself showed a copy of a 1707 letter from Leibniz to Jacob Hermann with the principle, but the original letter has been lost. In contentious proceedings, König was accused of forgery, and even the King of Prussia entered the debate, defending Maupertuis, while Voltaire
defended König. Euler, rather than claiming priority, was a staunch defender of Maupertuis, and Euler himself prosecuted König for forgery before the Berlin Academy on 13 April 1752.. The claims of forgery were re-examined 150 years later, and archival work by C.I. Gerhardt in 1898 and W. Kabitz in 1913 uncovered other copies of the letter, and three others cited by König, in the Bernoulli
archives.
, so that his statement of least action in statics is equivalent to the principle that a system of bodies at rest will adopt a configuration that minimizes total potential energy.
The full importance of the principle to mechanics was stated by Joseph Louis Lagrange
in 1760 (need ref), although the variational principle was not used to derive the equations of motion until almost 75 years later, when William Rowan Hamilton
in 1834 and 1835 applied the variational principle to the function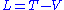
to obtain what are now called the Lagrangian equations of motion.
); most of his work focused on geodesics on two-dimensional surfaces . The first clear general statements were given by Marston Morse
in the 1920s and 1930s, leading to what is now known as Morse theory
. For example, Morse showed that the number of conjugate points in a trajectory equaled the number of negative eigenvalues in the second variation of the Lagrangian.
Other extremal principles of classical mechanics
have been formulated, such as Gauss' principle of least constraint and its corollary, Hertz's principle of least curvature.
which gives rise to the vacuum Einstein equations is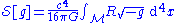
,
where
is the determinant of a spacetime Lorentz metric and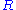 
is the scalar curvature
.
equations of motion and their integral
counterpart. The differential equations are statements about quantities localized to a single point in space or single moment of time. For example, Newton's second law
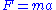states that the instantaneous force 
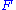applied to a mass 
produces an acceleration 
at the same instant. By contrast, the action principle is not localized to a point; rather, it involves integrals over an interval of time and (for fields) extended region of space. Moreover, in the usual formulation of classical
action principles, the initial and final states of the system are fixed, e.g.,
In particular, the fixing of the final state appears to give the action principle a teleological character
which has been controversial historically. This apparent teleology
is eliminated in the quantum mechanical
version of the action principle.
Variational principles among ancient Greeks
The earliest precedents of the principle of least action can be found in studies of the specular reflectionSpecular reflection
Specular reflection is the mirror-like reflection of light from a surface, in which light from a single incoming direction is reflected into a single outgoing direction...
and refraction
Refraction
Refraction is the change in direction of a wave due to a change in its speed. It is essentially a surface phenomenon . The phenomenon is mainly in governance to the law of conservation of energy. The proper explanation would be that due to change of medium, the phase velocity of the wave is changed...
of light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
. Hero of Alexandria
Hero of Alexandria
Hero of Alexandria was an ancient Greek mathematician and engineerEnc. Britannica 2007, "Heron of Alexandria" who was active in his native city of Alexandria, Roman Egypt...
noted that the law of reflection
Specular reflection
Specular reflection is the mirror-like reflection of light from a surface, in which light from a single incoming direction is reflected into a single outgoing direction...
follows from the assumption that light travels along the shortest distance between two given points.Variational principles in medieval times
This was generalized to refractionRefraction
Refraction is the change in direction of a wave due to a change in its speed. It is essentially a surface phenomenon . The phenomenon is mainly in governance to the law of conservation of energy. The proper explanation would be that due to change of medium, the phase velocity of the wave is changed...
by Pierre de Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
, who, in the 17th century, refined the principle to "light travels between two given points along the path of shortest time"; now known as the principle of least time or Fermat's principle
Fermat's principle
In optics, Fermat's principle or the principle of least time is the principle that the path taken between two points by a ray of light is the path that can be traversed in the least time. This principle is sometimes taken as the definition of a ray of light...
.
Euler
"Since the fabric of the Universe is most perfect and is the work of a most wise Creator, nothing whatsoever takes place in the Universe in which some relation of maximum and minimum does not appear."Principle of extremal action
Credit for the formulation of the principle of least action is commonly given to Pierre Louis MaupertuisPierre Louis Maupertuis
Pierre-Louis Moreau de Maupertuis was a French mathematician, philosopher and man of letters. He became the Director of the Académie des Sciences, and the first President of the Berlin Academy of Science, at the invitation of Frederick the Great....
, who wrote about it in 1744 and 1746, although the true priority is less clear, as discussed below.
Maupertuis felt that "Nature is thrifty in all its actions", and applied the principle broadly: "The laws of movement and of rest deduced from this principle being precisely the same as those observed in nature, we can admire the application of it to all phenomena. The movement of animals, the vegetative growth of plants ... are only its consequences; and the spectacle of the universe becomes so much the grander, so much more beautiful, the worthier of its Author, when one knows that a small number of laws, most wisely established, suffice for all movements."
In application to physics, Maupertuis suggested that the quantity to be minimized was the product of the duration (time) of movement within a system by the "vis viva
Vis viva
In the history of science, vis viva is an obsolete scientific theory that served as an elementary and limited early formulation of the principle of conservation of energy...
", twice what we now call the kinetic energy of the system.
Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
gave a formulation of the action principle in 1744, in very recognizable terms, in the Additamentum 2 to his "Methodus Inveniendi Lineas Curvas Maximi Minive Proprietate Gaudentes". He begins the second paragraph :
- "Sit massa corporis projecti
M, ejusque, dum spatiolum
ds emetitur, celeritas debita altitudiniv; erit quantitas motus corporis in hoc loco
; quae per ipsum spatiolum ds multiplicata, dabit 
motum corporis collectivum per spatiolum ds. Iam dico lineam a corpore descriptam ita fore comparatam, ut, inter omnes alias lineas iisdem terminis contentas, sit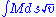 
, seu, ob M constans, 
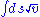minimum."
A translation of this passage reads:
- "Let the mass of the projectile be M, and let its squared velocity resulting from its height be v while being moved over a distance ds. The body will have a momentum
that, when multiplied by the distance ds, will give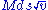 
, the momentum of the body integrated over the distance ds. Now I assert that the curve thus described by the body to be the curve (from among all other curves connecting the same endpoints) that minimizes 
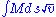or, provided that M is constant, 
."
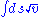As Euler states,
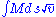is the integral of the momentum over distance traveled which, in modern notation, equals the reduced action . Thus, Euler made an equivalent and (apparently) independent statement of the variational principle in the same year as Maupertuis, albeit slightly later. Curiously, Euler did not claim any priority, as the following episode shows.Maupertuis' priority was disputed in 1751 by the mathematician Samuel König, who claimed that it had been invented by Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
in 1707. Although similar to many of Leibniz's arguments, the principle itself has not been documented in Leibniz's works. König himself showed a copy of a 1707 letter from Leibniz to Jacob Hermann with the principle, but the original letter has been lost. In contentious proceedings, König was accused of forgery, and even the King of Prussia entered the debate, defending Maupertuis, while Voltaire
Voltaire
François-Marie Arouet , better known by the pen name Voltaire , was a French Enlightenment writer, historian and philosopher famous for his wit and for his advocacy of civil liberties, including freedom of religion, free trade and separation of church and state...
defended König. Euler, rather than claiming priority, was a staunch defender of Maupertuis, and Euler himself prosecuted König for forgery before the Berlin Academy on 13 April 1752.. The claims of forgery were re-examined 150 years later, and archival work by C.I. Gerhardt in 1898 and W. Kabitz in 1913 uncovered other copies of the letter, and three others cited by König, in the Bernoulli
Bernoulli
The Bernoullis were a family of traders and scholars from Basel, Switzerland. The founder of the family, Leon Bernoulli, immigrated to Basel from Antwerp in Flanders in the 16th century, fleeing Spanish oppression....
archives.
Further developments of the extremal-action principle
Euler continued to write on the topic; in his Reflexions sur quelques loix generales de la nature (1748), he called the quantity "effort". His expression corresponds to what we would now call potential energyPotential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
, so that his statement of least action in statics is equivalent to the principle that a system of bodies at rest will adopt a configuration that minimizes total potential energy.
The full importance of the principle to mechanics was stated by Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
in 1760 (need ref), although the variational principle was not used to derive the equations of motion until almost 75 years later, when William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
in 1834 and 1835 applied the variational principle to the function
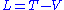to obtain what are now called the Lagrangian equations of motion.Other formulations of the extremal-action principle
In 1842, Carl Gustav Jacobi tackled the problem of whether the variational principle found minima or other extrema (e.g. a saddle pointSaddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
); most of his work focused on geodesics on two-dimensional surfaces . The first clear general statements were given by Marston Morse
Marston Morse
Harold Calvin Marston Morse was an American mathematician best known for his work on the calculus of variations in the large, a subject where he introduced the technique of differential topology now known as Morse theory...
in the 1920s and 1930s, leading to what is now known as Morse theory
Morse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
. For example, Morse showed that the number of conjugate points in a trajectory equaled the number of negative eigenvalues in the second variation of the Lagrangian.
Other extremal principles of classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
have been formulated, such as Gauss' principle of least constraint and its corollary, Hertz's principle of least curvature.
Variational principles in electromagnetism
The action for electromagnetism is:Variational principles in relativity theory
The Einstein-Hilbert actionEinstein-Hilbert action
The Einstein–Hilbert action in general relativity is the action that yields the Einstein's field equations through the principle of least action...
which gives rise to the vacuum Einstein equations is
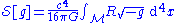,where
is the determinant of a spacetime Lorentz metric and 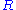is the scalar curvatureScalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
.
Variational principles in quantum mechanics
Sum over possible paths, Feynman approach. See Path integral formulationPath integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
Apparent teleology?
Although equivalent mathematically, there is an important philosophical difference between the differentialDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
equations of motion and their integral
Integral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
counterpart. The differential equations are statements about quantities localized to a single point in space or single moment of time. For example, Newton's second law
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
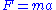states that the instantaneous force 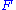applied to a mass produces an acceleration at the same instant. By contrast, the action principle is not localized to a point; rather, it involves integrals over an interval of time and (for fields) extended region of space. Moreover, in the usual formulation of classicalClassical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
action principles, the initial and final states of the system are fixed, e.g.,
- Given that the particle begins at position
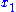at time 
and ends at position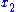 
at time 
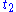, the physical trajectory that connects these two endpoints is an extremum of the action integral.
In particular, the fixing of the final state appears to give the action principle a teleological character
Teleology
A teleology is any philosophical account which holds that final causes exist in nature, meaning that design and purpose analogous to that found in human actions are inherent also in the rest of nature. The word comes from the Greek τέλος, telos; root: τελε-, "end, purpose...
which has been controversial historically. This apparent teleology
Teleology
A teleology is any philosophical account which holds that final causes exist in nature, meaning that design and purpose analogous to that found in human actions are inherent also in the rest of nature. The word comes from the Greek τέλος, telos; root: τελε-, "end, purpose...
is eliminated in the quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
version of the action principle.