
Hochschild homology
Encyclopedia
In mathematics
, Hochschild homology (and cohomology) is a homology theory
for associative algebras
over rings
. There is also a theory for Hochschild homology of certain functor
s. Hochschild cohomology was introduced by for algebras over a field, and extended to algebras over more general rings by .
, and M an A-bimodule
. The enveloping algebra of A is the tensor product Ae=A⊗Ao of A with its opposite algebra. Bimodules over A are essentially the same as modules over the enveloping algebra of A, so in particular A and M can be considered as Ae-modules. defined the Hochschild homology and cohomology group of A with coefficients in M in terms of the Tor functor
and Ext functor
by
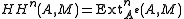
that is a projective k-module, and M an A-bimodule
. We will write A⊗n for the n-fold tensor product
of A over k. The chain complex
that gives rise to Hochschild homology is given by
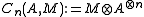
with boundary operator di defined by
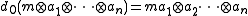
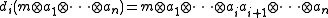
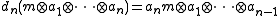
Here ai is in A for all 1 ≤ i ≤ n and m ∈ M. If we let
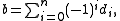
then b ° b = 0, so (Cn(A,M), b) is a chain complex
called the Hochschild complex, and its homology is the Hochschild homology of A with coefficients in M.
Cn(A,M) a simplicial object in the category
of k-modules, i.e. a functor Δo → k-mod, where Δ is the simplicial category
and k-mod is the category of k-modules. Here Δo is the opposite category
of Δ. The degeneracy maps are defined by si(a0 ⊗ ··· ⊗ an) = a0 ⊗ ··· ai ⊗ 1 ⊗ ai+1 ⊗ ··· ⊗ an. Hochschild homology is the homology of this simplicial module.
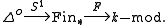
The homology of this simplicial module is the Hochschild homology of the functor F. The above definition of Hochschild homology of commutative algebras is the special case where F is the Loday functor.
for the category of finite pointed sets is given by the objects
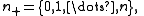
where 0 is the basepoint, and the morphisms are the basepoint preserving set maps. Let A be a commutative k-algebra and M be a symmetric A-bimodule. The Loday functor L(A,M) is given on objects in Fin* by
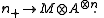
A morphism
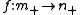
is sent to the morphism f* given by
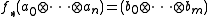
where
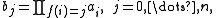
and bj = 1 if f −1(j) = ∅.

and this definition agrees with the one above.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Hochschild homology (and cohomology) is a homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
for associative algebras
Algebra (ring theory)
In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
over rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
. There is also a theory for Hochschild homology of certain functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s. Hochschild cohomology was introduced by for algebras over a field, and extended to algebras over more general rings by .
Definition of Hochschild homology of algebras
Let k be a ring, A an associative k-algebraAlgebra (ring theory)
In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
, and M an A-bimodule
Bimodule
In abstract algebra a bimodule is an abelian group that is both a left and a right module, such that the left and right multiplications are compatible...
. The enveloping algebra of A is the tensor product Ae=A⊗Ao of A with its opposite algebra. Bimodules over A are essentially the same as modules over the enveloping algebra of A, so in particular A and M can be considered as Ae-modules. defined the Hochschild homology and cohomology group of A with coefficients in M in terms of the Tor functor
Tor functor
In homological algebra, the Tor functors are the derived functors of the tensor product functor. They were first defined in generality to express the Künneth theorem and universal coefficient theorem in algebraic topology....
and Ext functor
Ext functor
In mathematics, the Ext functors of homological algebra are derived functors of Hom functors. They were first used in algebraic topology, but are common in many areas of mathematics.- Definition and computation :...
by

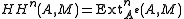
Hochschild complex
Let k be a ring, A an associative k-algebraAlgebra (ring theory)
In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
that is a projective k-module, and M an A-bimodule
Bimodule
In abstract algebra a bimodule is an abelian group that is both a left and a right module, such that the left and right multiplications are compatible...
. We will write A⊗n for the n-fold tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of A over k. The chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
that gives rise to Hochschild homology is given by
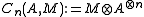
with boundary operator di defined by
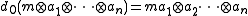
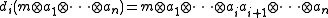
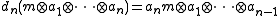
Here ai is in A for all 1 ≤ i ≤ n and m ∈ M. If we let
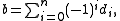
then b ° b = 0, so (Cn(A,M), b) is a chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
called the Hochschild complex, and its homology is the Hochschild homology of A with coefficients in M.
Remark
The maps di are face maps making the family of modulesModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
Cn(A,M) a simplicial object in the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of k-modules, i.e. a functor Δo → k-mod, where Δ is the simplicial category
Simplicial category
In mathematics, the simplex category is the category of finite ordinals and order preserving maps. It is used to define simplicial and cosimplicial objects.-Formal definition:...
and k-mod is the category of k-modules. Here Δo is the opposite category
Dual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
of Δ. The degeneracy maps are defined by si(a0 ⊗ ··· ⊗ an) = a0 ⊗ ··· ai ⊗ 1 ⊗ ai+1 ⊗ ··· ⊗ an. Hochschild homology is the homology of this simplicial module.
Hochschild homology of functors
The simplicial circle S1 is a simplicial object in the category Fin* of finite pointed sets, i.e. a functor Δo → Fin*. Thus, if F is a functor F: Fin → k-mod, we get a simplicial module by composing F with S1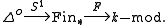
The homology of this simplicial module is the Hochschild homology of the functor F. The above definition of Hochschild homology of commutative algebras is the special case where F is the Loday functor.
Loday functor
A skeletonSkeleton (category theory)
In mathematics, a skeleton of a category is a subcategory which, roughly speaking, does not contain any extraneous isomorphisms. In a certain sense, the skeleton of a category is the "smallest" equivalent category which captures all "categorical properties". In fact, two categories are equivalent...
for the category of finite pointed sets is given by the objects
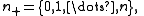
where 0 is the basepoint, and the morphisms are the basepoint preserving set maps. Let A be a commutative k-algebra and M be a symmetric A-bimodule. The Loday functor L(A,M) is given on objects in Fin* by
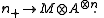
A morphism
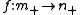
is sent to the morphism f* given by
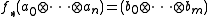
where
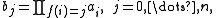
and bj = 1 if f −1(j) = ∅.
Another description of Hochschild homology of algebras
The Hochschild homology of a commutative algebra A with coefficients in a symmetric A-bimodule M is the homology associated to the composition
and this definition agrees with the one above.
External links
- Dylan G.L. Allegretti, The Cohomology of Noncommutative Spaces. An elementary introduction to noncommutative geometryNoncommutative geometryNoncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
which uses Hochschild homology to generalize differential forms). - Hochschild cohomology in ncatlab

