Hyperbolic absolute risk aversion
Encyclopedia
In finance
, economics
, and decision theory
, hyperbolic absolute risk aversion (HARA) refers to a type of risk aversion
that is particularly convenient to model mathematically and to obtain empirical predictions from. It refers specifically to a property of von Neumann-Morgenstern utility functions, which are typically functions of final wealth (or some related variable), and which describe a decision-maker's degree of satisfaction with the outcome for wealth. The final outcome for wealth is affected both by random variable
s and by decisions. Decision-makers are assumed to make their decisions (such as, for example, portfolio allocations
) so as to maximize the expected value
of the utility function.
Notable special cases of HARA utility functions include the quadratic utility function, the exponential utility function
, and the isoelastic utility function.
of absolute risk aversion A(W) — is a linear function of wealth W:
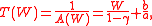
where A(W) is defined as –U "(W) / U '(W). A utility function U(W) has this property, and thus is a HARA utility function, if and only if it has the form
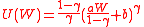
with restrictions on wealth and the parameters such that
and 
For a given parametrization, this restriction puts a lower bound on W if 
and an upper bound on W if 
. For the limiting case as 
→ 1, L'Hopital's Rule
shows that the utility function becomes linear in wealth; and for the limiting case as
goes to 0, the utility function becomes logarithmic: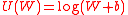 
.
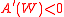(equivalently T '(W) > 0), which occurs if and only if 
is finite and less than 1; this is considered the empirically plausible case, since it implies that an investor will put more funds into risky assets the more funds are available to invest. Constant absolute risk aversion occurs as 
goes to positive or negative infinity, and the particularly implausible case of increasing absolute risk aversion occurs if 
is greater than one and finite.
, decreasing if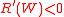 
, and constant if 
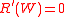. Thus relative risk aversion is increasing if b > 0 (for 
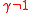), constant if b = 0, and decreasing if b < 0 (for 
).
a two-fund monetary separation theorem results: every investor holds the available risky assets in the same proportions as do all other investors, and investors differ from each other in their portfolio behavior only with regard to the fraction of their portfolios held in the risk-free asset rather than in the collection of risky assets.
Moreover, if an investor has a HARA utility function and a risk-free asset is available, then the investor's demands for the risk-free asset and all risky assets are linear in initial wealth.
In the capital asset pricing model
, there exists a representative investor utility function depending on the individual investors' utility functions and wealth levels, independent of the assets available, if and only if all investors have HARA utility functions with the same exponent. The representative utility function depends on the distribution of wealth, and one can describe market behavior as if there were a single investor with the representative utility function.
With a complete set of state-contingent securities, a sufficient condition for security prices in equilibrium
to be independent of the distribution of initial wealth holdings is that all investors have HARA utility functions with identical exponent and identical rate of time preference between beginning-of-period and end-of-period consumption.
of asset returns: to find the optimal current-period portfolio, one needs to know no future distributional information about the asset returns except the future risk-free returns.
With asset returns that are independently and identically distributed
through time and with a risk-free asset, risky asset proportions are independent of the investor's remaining lifetime.
and which are independently and identically distributed through time, and with a risk-free asset, one can obtain an explicit solution for the demand for the unique optimal mutual fund, and that demand is linear in initial wealth.
Finance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
, economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, and decision theory
Decision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
, hyperbolic absolute risk aversion (HARA) refers to a type of risk aversion
Risk aversion
Risk aversion is a concept in psychology, economics, and finance, based on the behavior of humans while exposed to uncertainty....
that is particularly convenient to model mathematically and to obtain empirical predictions from. It refers specifically to a property of von Neumann-Morgenstern utility functions, which are typically functions of final wealth (or some related variable), and which describe a decision-maker's degree of satisfaction with the outcome for wealth. The final outcome for wealth is affected both by random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s and by decisions. Decision-makers are assumed to make their decisions (such as, for example, portfolio allocations
Modern portfolio theory
Modern portfolio theory is a theory of investment which attempts to maximize portfolio expected return for a given amount of portfolio risk, or equivalently minimize risk for a given level of expected return, by carefully choosing the proportions of various assets...
) so as to maximize the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of the utility function.
Notable special cases of HARA utility functions include the quadratic utility function, the exponential utility function
Exponential utility
In economics exponential discounting is a specific form of the discount function, used in the analysis of choice over time...
, and the isoelastic utility function.
Definition
A utility function is said to exhibit hyperbolic absolute risk aversion if and only if the level of risk tolerance T(W) — the reciprocalReciprocal
-In mathematics:*Multiplicative inverse, in mathematics, the number 1/x, which multiplied by x gives the product 1, also known as a reciprocal*Reciprocal rule, a technique in calculus for calculating derivatives of reciprocal functions...
of absolute risk aversion A(W) — is a linear function of wealth W:
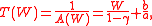
where A(W) is defined as –U "(W) / U '(W). A utility function U(W) has this property, and thus is a HARA utility function, if and only if it has the form
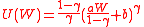
with restrictions on wealth and the parameters such that
and For a given parametrization, this restriction puts a lower bound on W if and an upper bound on W if . For the limiting case as → 1, L'Hopital's RuleL'Hôpital's rule
In calculus, l'Hôpital's rule uses derivatives to help evaluate limits involving indeterminate forms. Application of the rule often converts an indeterminate form to a determinate form, allowing easy evaluation of the limit...
shows that the utility function becomes linear in wealth; and for the limiting case as
goes to 0, the utility function becomes logarithmic: 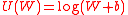.Decreasing, constant, and increasing absolute risk aversion
Absolute risk aversion is decreasing if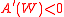 (equivalently T '(W) > 0), which occurs if and only if is finite and less than 1; this is considered the empirically plausible case, since it implies that an investor will put more funds into risky assets the more funds are available to invest. Constant absolute risk aversion occurs as goes to positive or negative infinity, and the particularly implausible case of increasing absolute risk aversion occurs if is greater than one and finite.Decreasing, constant, and increasing relative risk aversion
Relative risk aversion is defined as R(W)= WA(W); it is increasing if, decreasing if 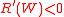, and constant if 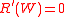. Thus relative risk aversion is increasing if b > 0 (for 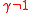), constant if b = 0, and decreasing if b < 0 (for ).Special cases
- Utility is linear (the risk neutral case) if
. - Utility is quadratic (an implausible though very mathematically tractable case, with increasing absolute risk aversion) if
. - The exponential utility functionExponential utilityIn economics exponential discounting is a specific form of the discount function, used in the analysis of choice over time...
, which has constant absolute risk aversion, occurs if b = 1 and
goes to negative infinity. - The power utility function occurs if
and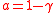 
. - The more special case of the isoelastic utility function, with constant relative risk aversion, occurs if, further, b = 0.
- The logarithmic utility function occurs for
as 
goes to 0. - The more special case of constant relative risk aversion equal to one — U(W) = log(W) — occurs if, further, b = 0.
Static portfolios
If all investors have HARA utility functions with the same exponent, then in the presence of a risk-free assetRisk-free interest rate
Risk-free interest rate is the theoretical rate of return of an investment with no risk of financial loss. The risk-free rate represents the interest that an investor would expect from an absolutely risk-free investment over a given period of time....
a two-fund monetary separation theorem results: every investor holds the available risky assets in the same proportions as do all other investors, and investors differ from each other in their portfolio behavior only with regard to the fraction of their portfolios held in the risk-free asset rather than in the collection of risky assets.
Moreover, if an investor has a HARA utility function and a risk-free asset is available, then the investor's demands for the risk-free asset and all risky assets are linear in initial wealth.
In the capital asset pricing model
Capital asset pricing model
In finance, the capital asset pricing model is used to determine a theoretically appropriate required rate of return of an asset, if that asset is to be added to an already well-diversified portfolio, given that asset's non-diversifiable risk...
, there exists a representative investor utility function depending on the individual investors' utility functions and wealth levels, independent of the assets available, if and only if all investors have HARA utility functions with the same exponent. The representative utility function depends on the distribution of wealth, and one can describe market behavior as if there were a single investor with the representative utility function.
With a complete set of state-contingent securities, a sufficient condition for security prices in equilibrium
Economic equilibrium
In economics, economic equilibrium is a state of the world where economic forces are balanced and in the absence of external influences the values of economic variables will not change. It is the point at which quantity demanded and quantity supplied are equal...
to be independent of the distribution of initial wealth holdings is that all investors have HARA utility functions with identical exponent and identical rate of time preference between beginning-of-period and end-of-period consumption.
Dynamic portfolios in discrete time
In a discrete time dynamic portfolio optimization context, under HARA utility optimal portfolio choice involves partial myopia if there is a risk-free asset and there is serial independenceAutocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
of asset returns: to find the optimal current-period portfolio, one needs to know no future distributional information about the asset returns except the future risk-free returns.
With asset returns that are independently and identically distributed
Independent and identically distributed random variables
In probability theory and statistics, a sequence or other collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent....
through time and with a risk-free asset, risky asset proportions are independent of the investor's remaining lifetime.
Dynamic portfolios in continuous time
With asset returns whose evolution is described by Brownian motionWiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
and which are independently and identically distributed through time, and with a risk-free asset, one can obtain an explicit solution for the demand for the unique optimal mutual fund, and that demand is linear in initial wealth.