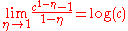Isoelastic utility
Encyclopedia
In economics
, the isoelastic function for utility, also known as the isoelastic utility function, constant relative risk aversion utility function, or power utility function, is used to express utility
in terms of consumption
or some other economic variable that a decision-maker is concerned with.
It is

where is consumption,
is consumption, 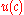 the associated utility, and
the associated utility, and  is a non-negative constant. Since additive constant terms in objective functions do not affect optimal decisions, the term –1 in the numerator can be, and usually is, omitted (except when establishing the limiting case of log(c) as below).
is a non-negative constant. Since additive constant terms in objective functions do not affect optimal decisions, the term –1 in the numerator can be, and usually is, omitted (except when establishing the limiting case of log(c) as below).
When the context involves risk, the utility function is viewed as a von Neumann-Morgenstern utility function, and the parameter is a measure of risk aversion.
is a measure of risk aversion.
The isoelastic utility function is a special case of the hyperbolic absolute risk aversion
(HARA) utility functions, and is used in analyses that either include or do not include underlying risk
.
 . While relatively high values of
. While relatively high values of  (as high as 50 in some models) are necessary to explain the behavior of asset prices, controlled experiments lead to the conclusion that individuals have
(as high as 50 in some models) are necessary to explain the behavior of asset prices, controlled experiments lead to the conclusion that individuals have  close to one.
close to one.
 is a constant, specifically
is a constant, specifically  . In theoretical models this often has the implication that decision-making is unaffected by scale. For instance, in the standard model of one risk-free asset and one risky asset, under constant relative risk aversion the fraction of wealth optimally placed in the risky asset is independent of the level of initial wealth.
. In theoretical models this often has the implication that decision-making is unaffected by scale. For instance, in the standard model of one risk-free asset and one risky asset, under constant relative risk aversion the fraction of wealth optimally placed in the risky asset is independent of the level of initial wealth.
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, the isoelastic function for utility, also known as the isoelastic utility function, constant relative risk aversion utility function, or power utility function, is used to express utility
Utility
In economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
in terms of consumption
Consumption (economics)
Consumption is a common concept in economics, and gives rise to derived concepts such as consumer debt. Generally, consumption is defined in part by comparison to production. But the precise definition can vary because different schools of economists define production quite differently...
or some other economic variable that a decision-maker is concerned with.
It is

where
 is consumption,
is consumption, 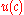 the associated utility, and
the associated utility, and  is a non-negative constant. Since additive constant terms in objective functions do not affect optimal decisions, the term –1 in the numerator can be, and usually is, omitted (except when establishing the limiting case of log(c) as below).
is a non-negative constant. Since additive constant terms in objective functions do not affect optimal decisions, the term –1 in the numerator can be, and usually is, omitted (except when establishing the limiting case of log(c) as below).When the context involves risk, the utility function is viewed as a von Neumann-Morgenstern utility function, and the parameter
 is a measure of risk aversion.
is a measure of risk aversion.The isoelastic utility function is a special case of the hyperbolic absolute risk aversion
Hyperbolic absolute risk aversion
In finance, economics, and decision theory, hyperbolic absolute risk aversion refers to a type of risk aversion that is particularly convenient to model mathematically and to obtain empirical predictions from...
(HARA) utility functions, and is used in analyses that either include or do not include underlying risk
Risk
Risk is the potential that a chosen action or activity will lead to a loss . The notion implies that a choice having an influence on the outcome exists . Potential losses themselves may also be called "risks"...
.
Empirical parametrization
There is substantial debate in the economics and finance literature with respect to the empirical value of . While relatively high values of
. While relatively high values of  (as high as 50 in some models) are necessary to explain the behavior of asset prices, controlled experiments lead to the conclusion that individuals have
(as high as 50 in some models) are necessary to explain the behavior of asset prices, controlled experiments lead to the conclusion that individuals have  close to one.
close to one.Risk aversion features
This and only this utility function has the feature of constant relative risk aversion. Mathematically this means that is a constant, specifically
is a constant, specifically  . In theoretical models this often has the implication that decision-making is unaffected by scale. For instance, in the standard model of one risk-free asset and one risky asset, under constant relative risk aversion the fraction of wealth optimally placed in the risky asset is independent of the level of initial wealth.
. In theoretical models this often has the implication that decision-making is unaffected by scale. For instance, in the standard model of one risk-free asset and one risky asset, under constant relative risk aversion the fraction of wealth optimally placed in the risky asset is independent of the level of initial wealth.Special cases
-
 : this corresponds to risk neutrality, because utility is linear in c.
: this corresponds to risk neutrality, because utility is linear in c. -
 : by virtue of l'Hôpital's ruleL'Hôpital's ruleIn calculus, l'Hôpital's rule uses derivatives to help evaluate limits involving indeterminate forms. Application of the rule often converts an indeterminate form to a determinate form, allowing easy evaluation of the limit...
: by virtue of l'Hôpital's ruleL'Hôpital's ruleIn calculus, l'Hôpital's rule uses derivatives to help evaluate limits involving indeterminate forms. Application of the rule often converts an indeterminate form to a determinate form, allowing easy evaluation of the limit...
, the limit of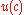 is
is  as
as  goes to one:
goes to one:
-
- which justifies the convention of using the limiting value u(c) = log c when
 .
.
-
 →
→  : this is the case of infinite risk aversion.
: this is the case of infinite risk aversion.
-
See also
- Isoelastic functionIsoelastic functionIn mathematical economics, an isoelastic function, sometimes constant elasticity function, is a function that exhibits a constant elasticity, i.e. has a constant elasticity coefficient...
- Constant elasticity of substitutionConstant Elasticity of SubstitutionIn economics, Constant elasticity of substitution is a property of some production functions and utility functions.More precisely, it refers to a particular type of aggregator function which combines two or more types of consumption, or two or more types of productive inputs into an aggregate...
- Exponential utilityExponential utilityIn economics exponential discounting is a specific form of the discount function, used in the analysis of choice over time...
- Risk aversionRisk aversionRisk aversion is a concept in psychology, economics, and finance, based on the behavior of humans while exposed to uncertainty....