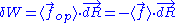
Ideal chain
Encyclopedia
An ideal chain is the simplest model to describe a polymer
. It only assumes a polymer as a random walk
and neglects any kind of interactions among monomers. Although it is simple, its generality gives us some insights about the physics
of polymers.
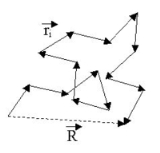
In this model, monomers are rigid rods of a fixed length l, and their orientation is completely independent of the orientations and positions of neighbouring monomers, to the extent that two monomers can co-exist at the same place.
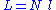, where N is the number of monomers.
In this very simple approach where no interactions between monomers are considered, the energy of the polymer is taken to be independent of its shape, which means that at thermodynamic equilibrium
, all of its shape configurations are equally likely to occur as the polymer fluctuates in time, according to the Maxwell-Boltzmann distribution.
Let us call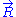
the total end to end vector of an ideal chain and 
the vectors corresponding to individual monomer
s. Those random vectors have components in the three directions of space. Most of the expressions given in this article assume that the number of monomers N is large, so that the central limit theorem
applies. The figure below shows a sketch of a (short) ideal chain.
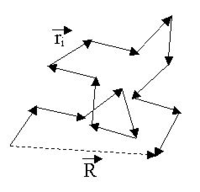The two ends of the chain are not coincident, but they fluctuate around each other, so that of course: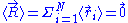
Throughout the article the
brackets will be used to denote the mean
(of values taken over time) of a random variable or a random vector, as above.
Since
are independent
, it follows from the Central limit theorem
that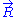
is distributed according to a normal distribution (or gaussian distribution): precisely, in 3D, 
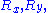and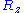 
are distributed according to a normal distribution of mean
0 and of variance
:
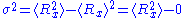
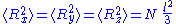
So that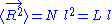
. The end to end vector of the chain is distributed according to the following probability density function
:
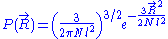
The average end-to-end distance of the polymer is:
A quantity frequently used in polymer physics is the radius of gyration:
It is worth noting that the above average end-to-end distance, which in the case of this simple model is also the typical amplitude of the system's fluctuations, becomes negligible compared to the total unfolded length of the polymer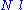
at the thermodynamic limit
. This result is a general property of statistical systems.
Mathematical remark: the rigorous demonstration of the expression of the density of probability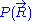
is not as direct as it appears above: from the application of the usual (1D) central limit theorem
one can deduce that
, 
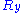and 
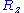are distributed according to a centered normal distribution of variance 
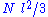. Then, the expression given above for 
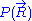is not the only one that is compatible with such distribution for 
, 
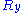and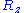 
. However, since the components of the vectors 
are uncorrelated
for the random walk we are considering, it follows that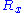
, 
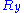and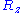 
are also uncorrelated
. This additional condition can only be fulfilled if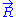
is distributed according to 
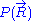. Alternatively, this result can also be demonstrated by applying a multidimensional generalization of the central limit theorem
, or through symmetry
arguments.
The relevancy of the model is, however, limited, even at the macroscopic scale, by the fact that it does not consider any excluded volume for monomers (or, to speak in chemical terms, that it neglects steric effects
).
Other fluctuating polymer models that consider no interaction between monomers and no excluded volume, like the worm-like chain
model, are all asymptotically convergent toward this model at the thermodynamic limit
. For purpose of this analogy a Kuhn segment
is introduced, corresponding to the equivalent monomer length to be considered in the analogous ideal chain. The number of Kuhn segments to be considered in the analogous ideal chain is equal to the total unfolded length of the polymer divided by the length of a Kuhn segment.
, is also constant, which means that this force necessarily stems from a purely entropic
effect.
This entropic force is very similar to the pressure experienced by the walls of a box containing an ideal gas
. The internal energy
of an ideal gas
depends only on its temperature, and not on the volume of its containing box, so it is not an energy
effect that tends to increase the volume of the box like gas pressure
does. This implies that the pressure
of an ideal gas has a purely entropic
origin.
What is the microscopic origin of such an entropic
force or pressure? The most general answer is that the effect of thermal fluctuations tends to bring a thermodynamic system toward a macroscopic state that corresponds to a maximum in the number of microscopic states (or micro-states) that are compatible with this macroscopic state. In other words, thermal fluctuations tend to bring a system toward its macroscopic state of maximum entropy
.
What does this mean in the case of the ideal chain? First, for our ideal chain, a microscopic state is characterized by the superposition of the states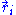
of each individual monomer (with i varying from 1 to N). In its solvent, the ideal chain is constantly subject to shocks from moving solvent molecules, and each of these shocks sends the system from its current microscopic state to another, very similar microscopic state. For an ideal polymer, as will be shown below, there are more microscopic states compatible with a short end-to-end distance than there are microscopic states compatible with a large end-to-end distance. Thus, for an ideal chain, maximizing its entropy
means reducing the distance between its two free ends. Consequently, a force that tends to collapse the chain is exerted by the ideal chain between its two free ends.
In this section, the mean
of this force will be derived. The generality of the expression obtained at the thermodynamic limit
will then be discussed.
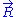joining these two points characterizes the macroscopic state (or macro-state) of the ideal chain. To each macro-state corresponds a certain number of micro-states, that we will call 
(micro-states are defined in the introduction to this section). Since the ideal chain's energy
is constant, each of these micro-states is equally likely to occur. The entropy
associated to a macro-state is thus equal to: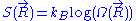
, where 
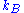is Boltzmann's constant
The above expression gives the absolute (quantum) entropy
of the system. A precise determination of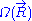
would require a quantum model for the ideal chain, which is beyond the scope of this article. However, we have already calculated the probability density 
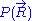associated with the end-to-end vector of the unconstrained ideal chain, above. Since all micro-states of the ideal chain are equally likely to occur, 
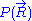is proportional to 
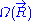. This leads to the following expression for the classical (relative) entropy
of the ideal chain: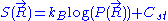
,
where
is a fixed constant. Let us call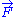 
the force exerted by the chain on the point to which its end is attached. From the above expression of the entropy
, we can deduce an expression of this force. Suppose that, instead of being fixed, the positions of the two ends of the ideal chain are now controlled by an operator. The operator controls the evolution of the end to end vector
. If the operator changes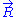 
by a tiny amount 
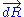, then the variation of internal energy
of the chain is null, since the energy
of the chain is constant. This condition can be written as: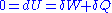
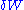is defined as the elementary amount of mechanical work
transferred by the operator to the ideal chain, and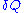
is defined as the elementary amount of heat
transferred by the solvent to the ideal chain. Now, if we assume that the transformation imposed by the operator on the system is quasistatic (i.e., infinitely slow), then the system's transformation will be time-reversible, and we can assume that during its passage from macro-state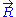
to macro-state 
, the system passes through a series of thermodynamic equilibrium
macro-states. This has two consequences:
We are thus led to:
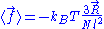
The above equation is the equation of state
of the ideal chain. Since the expression depends on the central limit theorem
, it is only exact in the limit of polymers containing a large number of monomers (that is, the thermodynamic limit
). It is also only valid for small end-to-end distances, relative to the overall polymer contour length, where the behavior is like a hookean spring. Behavior over larger force ranges can be modeled using a canonical ensemble treatment identical to magnetization of paramagnetic spins. Finally, the model can be extended to even larger force ranges by inclusion of a stretch modulus along the polymer contour length. That is, by allowing the length of each unit of the chain to respond elastically to the applied force.
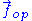on the ideal chain. In this case the two ends of the polymer fluctuate around a mean
position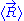
. The ideal chain reacts with a constant opposite force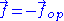 
For an ideal chain exchanging length with a reservoir, a macro-state of the system is characterized by the vector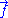
.
The change between an ideal chain of fixed length and an ideal chain in contact with a length reservoir is very much akin to the change between the micro-canonical ensemble and the canonical ensemble (see the Statistical mechanics
article about this). The change is from a state where a fixed value is imposed on a certain parameter, to a state where the system is left free to exchange this parameter with the outside. The parameter in question is energy for the microcanonical and canonical descriptions, whereas in the case of the ideal chain the parameter is the length of the ideal chain.
Like for the micro-canonical and canonical ensembles, the two descriptions of the ideal chain differ only in the way they treat the system's fluctuations. They are thus equivalent at the thermodynamic limit
. The equation of state
of the ideal chain remains the same, except that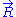
is now subject to fluctuations:
.
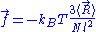Polymer
A polymer is a large molecule composed of repeating structural units. These subunits are typically connected by covalent chemical bonds...
. It only assumes a polymer as a random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
and neglects any kind of interactions among monomers. Although it is simple, its generality gives us some insights about the physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
of polymers.
In this model, monomers are rigid rods of a fixed length l, and their orientation is completely independent of the orientations and positions of neighbouring monomers, to the extent that two monomers can co-exist at the same place.
The model
N monomers form the polymer, whose total unfolded length is: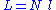, where N is the number of monomers.In this very simple approach where no interactions between monomers are considered, the energy of the polymer is taken to be independent of its shape, which means that at thermodynamic equilibrium
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
, all of its shape configurations are equally likely to occur as the polymer fluctuates in time, according to the Maxwell-Boltzmann distribution.
Let us call
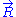the total end to end vector of an ideal chain and the vectors corresponding to individual monomerMonomer
A monomer is an atom or a small molecule that may bind chemically to other monomers to form a polymer; the term "monomeric protein" may also be used to describe one of the proteins making up a multiprotein complex...
s. Those random vectors have components in the three directions of space. Most of the expressions given in this article assume that the number of monomers N is large, so that the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
applies. The figure below shows a sketch of a (short) ideal chain.
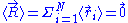
Throughout the article the
brackets will be used to denote the meanMean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
(of values taken over time) of a random variable or a random vector, as above.
Since
are independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
, it follows from the Central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
that
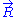is distributed according to a normal distribution (or gaussian distribution): precisely, in 3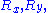D, and 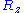are distributed according to a normal distribution of meanMean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
0 and of variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
:
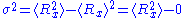
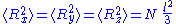
So that
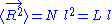. The end to end vector of the chain is distributed according to the following probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
:
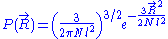
The average end-to-end distance of the polymer is:
A quantity frequently used in polymer physics is the radius of gyration:
It is worth noting that the above average end-to-end distance, which in the case of this simple model is also the typical amplitude of the system's fluctuations, becomes negligible compared to the total unfolded length of the polymer
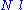at the thermodynamic limitThermodynamic limit
In thermodynamics, particularly statistical mechanics, the thermodynamic limit is reached as the number of particles in a system, N, approaches infinity...
. This result is a general property of statistical systems.
Mathematical remark: the rigorous demonstration of the expression of the density of probability
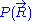is not as direct as it appears above: from the application of the usual (1D) central limit theoremCentral limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
one can deduce that
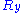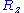, and are distributed according to a centered normal distribution of variance 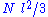. Then, the expression given above for 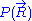is not the only one that is compatible with such distribution for , 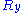and 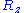. However, since the components of the vectors are uncorrelatedCorrelation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
for the random walk we are considering, it follows that
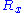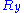, and 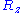are also uncorrelatedCorrelation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
. This additional condition can only be fulfilled if
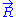is distributed according to 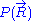. Alternatively, this result can also be demonstrated by applying a multidimensional generalization of the central limit theoremCentral limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
, or through symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
arguments.
Generality of the model
While the elementary model described above is totally unadapted to the description of real-world polymers at the microscopic scale, it does show some relevance at the macroscopic scale in the case of a polymer in solution whose monomers form an ideal mix with the solvent (in which case, the interactions between monomer and monomer, solvent molecule and solvent molecule, and between monomer and solvent are identical, and the system's energy can be considered constant, validating the hypothesis of the model).The relevancy of the model is, however, limited, even at the macroscopic scale, by the fact that it does not consider any excluded volume for monomers (or, to speak in chemical terms, that it neglects steric effects
Steric effects
Steric effects arise from the fact that each atom within a molecule occupies a certain amount of space. If atoms are brought too close together, there is an associated cost in energy due to overlapping electron clouds , and this may affect the molecule's preferred shape and reactivity.-Steric...
).
Other fluctuating polymer models that consider no interaction between monomers and no excluded volume, like the worm-like chain
Worm-like chain
The worm-like chain model in polymer physics is used to describe the behavior of semi-flexible polymers; it is sometimes referred to as the Kratky-Porod model.- Theoretical Considerations :...
model, are all asymptotically convergent toward this model at the thermodynamic limit
Thermodynamic limit
In thermodynamics, particularly statistical mechanics, the thermodynamic limit is reached as the number of particles in a system, N, approaches infinity...
. For purpose of this analogy a Kuhn segment
Kuhn length
The Kuhn length is a theoretical treatment, developed by Werner Kuhn, in which a real polymer chain is considered as a collection of N Kuhn segments each with a Kuhn length b. Each Kuhn segment can be thought of as if they are freely jointed with each other...
is introduced, corresponding to the equivalent monomer length to be considered in the analogous ideal chain. The number of Kuhn segments to be considered in the analogous ideal chain is equal to the total unfolded length of the polymer divided by the length of a Kuhn segment.
Entropic elasticity of an ideal chain
If the two free ends of an ideal chain are attached to some kind of micro-manipulation device, then the device experiences a force exerted by the polymer. The ideal chain's energy is constant, and thus its time-average, the internal energyInternal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
, is also constant, which means that this force necessarily stems from a purely entropic
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
effect.
This entropic force is very similar to the pressure experienced by the walls of a box containing an ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
. The internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
of an ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
depends only on its temperature, and not on the volume of its containing box, so it is not an energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
effect that tends to increase the volume of the box like gas pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
does. This implies that the pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
of an ideal gas has a purely entropic
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
origin.
What is the microscopic origin of such an entropic
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
force or pressure? The most general answer is that the effect of thermal fluctuations tends to bring a thermodynamic system toward a macroscopic state that corresponds to a maximum in the number of microscopic states (or micro-states) that are compatible with this macroscopic state. In other words, thermal fluctuations tend to bring a system toward its macroscopic state of maximum entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
.
What does this mean in the case of the ideal chain? First, for our ideal chain, a microscopic state is characterized by the superposition of the states
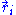of each individual monomer (with i varying from 1 to N). In its solvent, the ideal chain is constantly subject to shocks from moving solvent molecules, and each of these shocks sends the system from its current microscopic state to another, very similar microscopic state. For an ideal polymer, as will be shown below, there are more microscopic states compatible with a short end-to-end distance than there are microscopic states compatible with a large end-to-end distance. Thus, for an ideal chain, maximizing its entropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
means reducing the distance between its two free ends. Consequently, a force that tends to collapse the chain is exerted by the ideal chain between its two free ends.
In this section, the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
of this force will be derived. The generality of the expression obtained at the thermodynamic limit
Thermodynamic limit
In thermodynamics, particularly statistical mechanics, the thermodynamic limit is reached as the number of particles in a system, N, approaches infinity...
will then be discussed.
Ideal chain under length constraint
The case of an ideal chain whose two ends are attached to fixed points will be considered in this sub-section. The vector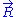 joining these two points characterizes the macroscopic state (or macro-state) of the ideal chain. To each macro-state corresponds a certain number of micro-states, that we will call (micro-states are defined in the introduction to this section). Since the ideal chain's energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
is constant, each of these micro-states is equally likely to occur. The entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
associated to a macro-state is thus equal to:
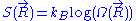, where 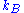is Boltzmann's constantThe above expression gives the absolute (quantum) entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of the system. A precise determination of
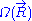would require a quantum model for the ideal chain, which is beyond the scope of this article. However, we have already calculated the probability density 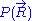associated with the end-to-end vector of the unconstrained ideal chain, above. Since all micro-states of the ideal chain are equally likely to occur, 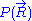is proportional to 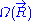. This leads to the following expression for the classical (relative) entropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of the ideal chain:
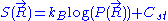,where
is a fixed constant. Let us call 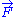the force exerted by the chain on the point to which its end is attached. From the above expression of the entropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
, we can deduce an expression of this force. Suppose that, instead of being fixed, the positions of the two ends of the ideal chain are now controlled by an operator. The operator controls the evolution of the end to end vector
. If the operator changes 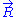by a tiny amount 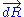, then the variation of internal energyInternal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
of the chain is null, since the energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
of the chain is constant. This condition can be written as:
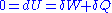
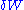is defined as the elementary amount of mechanical workMechanical work
In physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work...
transferred by the operator to the ideal chain, and
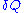is defined as the elementary amount of heatHeat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
transferred by the solvent to the ideal chain. Now, if we assume that the transformation imposed by the operator on the system is quasistatic (i.e., infinitely slow), then the system's transformation will be time-reversible, and we can assume that during its passage from macro-state
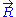to macro-state , the system passes through a series of thermodynamic equilibriumThermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
macro-states. This has two consequences:
- first, the amount of heatHeatIn physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
received by the system during the transformation can be tied to the variation of its entropyEntropyEntropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
:
-
-
, where T is the temperature of the chain.
-
- second, in order for the transformation to remain infinitely slow, the meanMeanIn statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
force exerted by the operator on the end points of the chain must balance the meanMeanIn statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
force exerted by the chain on its end points. Calling
the force exerted by the operator and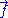 
the force exerted by the chain, we have:
We are thus led to:
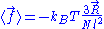
The above equation is the equation of state
Equation of state
In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...
of the ideal chain. Since the expression depends on the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
, it is only exact in the limit of polymers containing a large number of monomers (that is, the thermodynamic limit
Thermodynamic limit
In thermodynamics, particularly statistical mechanics, the thermodynamic limit is reached as the number of particles in a system, N, approaches infinity...
). It is also only valid for small end-to-end distances, relative to the overall polymer contour length, where the behavior is like a hookean spring. Behavior over larger force ranges can be modeled using a canonical ensemble treatment identical to magnetization of paramagnetic spins. Finally, the model can be extended to even larger force ranges by inclusion of a stretch modulus along the polymer contour length. That is, by allowing the length of each unit of the chain to respond elastically to the applied force.
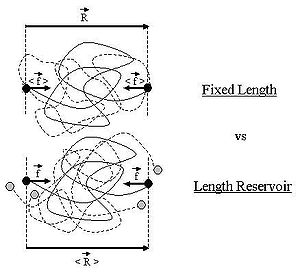
Ideal polymer exchanging length with a reservoir
Throughout this sub-section, as in the previous one, the two ends of the polymer are attached to a micro-manipulation device. This time, however, the device does not maintain the two ends of the ideal chain in a fixed position, but rather it maintains a constant pulling force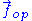 on the ideal chain. In this case the two ends of the polymer fluctuate around a meanMean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
position
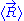. The ideal chain reacts with a constant opposite force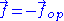 For an ideal chain exchanging length with a reservoir, a macro-state of the system is characterized by the vector
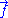.The change between an ideal chain of fixed length and an ideal chain in contact with a length reservoir is very much akin to the change between the micro-canonical ensemble and the canonical ensemble (see the Statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
article about this). The change is from a state where a fixed value is imposed on a certain parameter, to a state where the system is left free to exchange this parameter with the outside. The parameter in question is energy for the microcanonical and canonical descriptions, whereas in the case of the ideal chain the parameter is the length of the ideal chain.
Like for the micro-canonical and canonical ensembles, the two descriptions of the ideal chain differ only in the way they treat the system's fluctuations. They are thus equivalent at the thermodynamic limit
Thermodynamic limit
In thermodynamics, particularly statistical mechanics, the thermodynamic limit is reached as the number of particles in a system, N, approaches infinity...
. The equation of state
Equation of state
In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...
of the ideal chain remains the same, except that
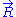is now subject to fluctuations: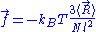.See also
- PolymerPolymerA polymer is a large molecule composed of repeating structural units. These subunits are typically connected by covalent chemical bonds...
- Worm-like chainWorm-like chainThe worm-like chain model in polymer physics is used to describe the behavior of semi-flexible polymers; it is sometimes referred to as the Kratky-Porod model.- Theoretical Considerations :...
, a more complex polymer model - Kuhn lengthKuhn lengthThe Kuhn length is a theoretical treatment, developed by Werner Kuhn, in which a real polymer chain is considered as a collection of N Kuhn segments each with a Kuhn length b. Each Kuhn segment can be thought of as if they are freely jointed with each other...
- Coil-globule transitionCoil-globule transitionIn polymer physics, the Coil-globule transition is the collapse of a macromolecule from an expanded coil state through an ideal coil state to a collapsed globule state, or vice-versa. The coil-globule transition is of importance in biology due to the presence of coil-globule transitions in...