Initial value formulation (general relativity)
Encyclopedia
The initial value formulation of general relativity is a reformulation of Albert Einstein
's theory of general relativity
that describes a universe
evolving over time
.
Each solution of the Einstein field equations
encompasses the whole history of a universe – it is not just some snapshot of how things are, but a whole spacetime
: a statement encompassing the state of matter and geometry everywhere and at every moment in that particular universe. By this token, Einstein's theory appears to be different from most other physical theories, which specify evolution equations for physical systems; if the system is in a given state at some given moment, the laws of physics allow you to extrapolate its past or future. For Einstein's equations, there appear to be subtle differences compared with other fields: they are self-interacting (that is, non-linear even in the absence of other fields; they are diffeomorphism invariant, so to obtain a unique solution, a fixed background metric and gauge conditions need to be introduced; finally, the metric determines the spacetime structure, and thus the domain of dependence for any set of initial data, so the region on which a specific solution will be defined is not, a priori, defined.
There is, however, a way to re-formulate Einstein's equations that overcomes these problems. First of all, there are ways of rewriting spacetime as the evolution of "space" in time; an earlier version of this is due to Paul Dirac
, while a simpler way is known after its inventors Richard Arnowitt
, Stanley Deser
and Charles Misner as ADM formalism
. In these formulations, also known as "3+1" approaches, spacetime is split into a three-dimensional hypersurface with interior metric and an embedding into spacetime with exterior curvature; these two quantities are the dynamical variables in a Hamiltonian
formulation tracing the hypersurface's evolution over time. With such a split, it is possible to state the initial value formulation of general relativity. It involves initial data which cannot be specified arbitrarily but needs to satisfy specific constraint
equations, and which is defined on some suitably smooth three-manifold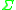
; just as for other differential equations, it is then possible to prove existence
and uniqueness
theorems, namely that there exists a unique spacetime which is a solution of Einstein equations, which is globally hyperbolic, for which
is a Cauchy surface
(i.e. all past events influence what happens on
, and all future events are influenced by what happens on it), and has the specified internal metric and extrinsic curvature; all spacetimes that satisfy these conditions are related by isometries
.
The initial value formulation with its 3+1 split is the basis of numerical relativity
; attempts to simulate the evolution of relativistic spacetimes (notably merging black hole
s or gravitational collapse
) using computers. However, there are significant differences to the simulation of other physical evolution equations which make numerical relativity especially challenging, notably the fact that the dynamical objects that are evolving include space and time itself (so there is no fixed background against which to evaluate, for instance, perturbations representing gravitational waves) and the occurrence of singularities (which, when they are allowed to occur within the simulated portion of spacetime, lead to arbitrarily large numbers that would have to be represented in the computer model).
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
's theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
that describes a universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
evolving over time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
.
Each solution of the Einstein field equations
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
encompasses the whole history of a universe – it is not just some snapshot of how things are, but a whole spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
: a statement encompassing the state of matter and geometry everywhere and at every moment in that particular universe. By this token, Einstein's theory appears to be different from most other physical theories, which specify evolution equations for physical systems; if the system is in a given state at some given moment, the laws of physics allow you to extrapolate its past or future. For Einstein's equations, there appear to be subtle differences compared with other fields: they are self-interacting (that is, non-linear even in the absence of other fields; they are diffeomorphism invariant, so to obtain a unique solution, a fixed background metric and gauge conditions need to be introduced; finally, the metric determines the spacetime structure, and thus the domain of dependence for any set of initial data, so the region on which a specific solution will be defined is not, a priori, defined.
There is, however, a way to re-formulate Einstein's equations that overcomes these problems. First of all, there are ways of rewriting spacetime as the evolution of "space" in time; an earlier version of this is due to Paul Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
, while a simpler way is known after its inventors Richard Arnowitt
Richard Arnowitt
Richard Lewis Arnowitt is an American physicist known for his contributions to theoretical particle physics and to general relativity.Arnowitt is a Distinguished Professor at Texas A&M University, where he is a member of the Department of Physics....
, Stanley Deser
Stanley Deser
Stanley Deser is an American physicist known for his contributions to general relativity. Currently, he is the Ancell Professor of Physics at Brandeis University in Waltham, Massachusetts....
and Charles Misner as ADM formalism
ADM formalism
The ADM Formalism developed in 1959 by Richard Arnowitt, Stanley Deser and Charles W. Misner is a Hamiltonian formulation of general relativity...
. In these formulations, also known as "3+1" approaches, spacetime is split into a three-dimensional hypersurface with interior metric and an embedding into spacetime with exterior curvature; these two quantities are the dynamical variables in a Hamiltonian
Hamiltonian
Hamiltonian may refer toIn mathematics :* Hamiltonian system* Hamiltonian path, in graph theory** Hamiltonian cycle, a special case of a Hamiltonian path* Hamiltonian group, in group theory* Hamiltonian...
formulation tracing the hypersurface's evolution over time. With such a split, it is possible to state the initial value formulation of general relativity. It involves initial data which cannot be specified arbitrarily but needs to satisfy specific constraint
Constraint (mathematics)
In mathematics, a constraint is a condition that a solution to an optimization problem must satisfy. There are two types of constraints: equality constraints and inequality constraints...
equations, and which is defined on some suitably smooth three-manifold
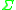; just as for other differential equations, it is then possible to prove existenceExistence theorem
In mathematics, an existence theorem is a theorem with a statement beginning 'there exist ..', or more generally 'for all x, y, ... there exist ...'. That is, in more formal terms of symbolic logic, it is a theorem with a statement involving the existential quantifier. Many such theorems will not...
and uniqueness
Uniqueness theorem
The uniqueness theorem for Poisson's equation states that the equation has a unique gradient of the solution for a large class of boundary conditions...
theorems, namely that there exists a unique spacetime which is a solution of Einstein equations, which is globally hyperbolic, for which
is a Cauchy surfaceCauchy surface
Intuitively, a Cauchy surface is a plane in space-time which is like an instant of time; its significance is that giving the initial conditions on this plane determines the future uniquely....
(i.e. all past events influence what happens on
, and all future events are influenced by what happens on it), and has the specified internal metric and extrinsic curvature; all spacetimes that satisfy these conditions are related by isometriesIsometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
.
The initial value formulation with its 3+1 split is the basis of numerical relativity
Numerical relativity
Numerical relativity is one of the branches of general relativity that uses numerical methods and algorithms to solve and analyze problems. To this end, supercomputers are often employed to study black holes, gravitational waves, neutron stars and many other phenomena governed by Einstein's Theory...
; attempts to simulate the evolution of relativistic spacetimes (notably merging black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
s or gravitational collapse
Gravitational collapse
Gravitational collapse is the inward fall of a body due to the influence of its own gravity. In any stable body, this gravitational force is counterbalanced by the internal pressure of the body, in the opposite direction to the force of gravity...
) using computers. However, there are significant differences to the simulation of other physical evolution equations which make numerical relativity especially challenging, notably the fact that the dynamical objects that are evolving include space and time itself (so there is no fixed background against which to evaluate, for instance, perturbations representing gravitational waves) and the occurrence of singularities (which, when they are allowed to occur within the simulated portion of spacetime, lead to arbitrarily large numbers that would have to be represented in the computer model).