Inoue surface
Encyclopedia
In complex geometry
, a part of mathematics, the term
Inoue surface denotes several complex surfaces
of Kodaira class VII. They are
named after Masahisa Inoue, who gave the first non-trivial
examples of Kodaira class VII surfaces in 1974.
The Inoue surfaces are not Kähler manifold
s.
S+ and S−, which are compact quotients
of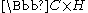
(a product of a complex
plane by a half-plane). These Inoue surfaces are
solvmanifold
s. They are obtained as quotients of
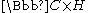by a solvable discrete
group which acts holomorphically on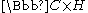
.
The solvmanifold surfaces constructed by Inoue all have second Betti number
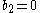. These surfaces are of Kodaira class VII,
which means that they have
and Kodaira dimension
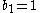. It was proven by Bogomolov
, Li-Yau
and Teleman that any surface of class VII
with b2 = 0 is a Hopf surface
or an Inoue-type solvmanifold.
These surfaces have no meromorphic functions and no curves.
K. Hasegawa gives a list of all complex 2-dimensional solvmanifolds; these are complex torus
, hyperelliptic surface
, Kodaira surface
and
Inoue surfaces S0, S+ and S−.
The Inoue surfaces are constructed explicitly as follows.
two complex eigenvalues
and a real eigenvalue c, with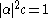
.
Then φ is invertible over integers, and defines an
action of the group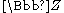
of integers on
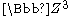. Let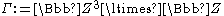 
.
This group is a lattice in solvable
Lie group
acting on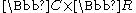
, with
the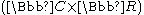
-part
acting by translations and the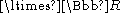
-part
as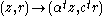
.
We extend this action to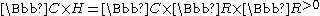
by setting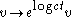
,
where t is the parameter of the
-part of
,
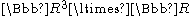and acting trivially with the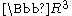
factor on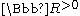
. This action
is clearly holomorphic, and the quotient
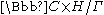is called
Inoue surface of type S0.
The Inoue surface of type S0 is determined by the choice of an integer matrix φ, constrained as above. There is a countable number of such surfaces.
and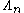
be the group of upper
triangular matrices
where x, y, z are integers. Consider an
automorphism of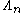
, denoted as φ.
The quotient of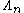
by
its center C is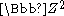
.
We assume that φ acts on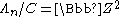
as a matrix with two positive real eigenvalues
a, b, and ab = 1.
Consider the solvable group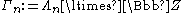
,
with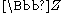
acting on 
as φ. Identifying the group of upper triangular
matrices with
, we obtain an
action of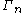
on
.
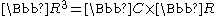Define an action of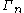
on
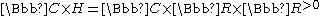
with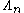
acting trivially on
the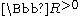
-part and the
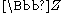acting as 
.
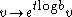The same argument as for Inoue surfaces of type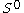
shows that this action is holomorphic. The
quotient
is called Inoue surface of type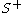
.
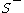
are defined in the same was as for S+, but
two eigenvalues a, b of φ acting on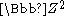
have opposite sign and satisfy ab = −1. Since a square of such an
endomorphism defines an Inoue surface of type S+,
an Inoue surface of type S− has an
unramified double cover of type S+.
Kodaira class VII surfaces defined by Iku Nakamura
in 1984. They are not solvmanifolds.
These surfaces have positive second Betti number.
They have spherical shells, and can be deformed
into a blown-up Hopf surface
.
Parabolic Inoue surfaces are also known
as half-Inoue surfaces. These surfaces can be defined
as class VII0 (that is, class VII and
minimal
) surfaces with
an elliptic curve
and a cycle of rational curves.
Hyperbolic Inoue surfaces are class VII0
surfaces with two cycles of rational curves.
Complex geometry
In mathematics, complex geometry is the study of complex manifolds and functions of many complex variables. Application of transcendental methods to algebraic geometry falls in this category, together with more geometric chapters of complex analysis....
, a part of mathematics, the term
Inoue surface denotes several complex surfaces
of Kodaira class VII. They are
named after Masahisa Inoue, who gave the first non-trivial
examples of Kodaira class VII surfaces in 1974.
The Inoue surfaces are not Kähler manifold
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
s.
Inoue surfaces with b2 = 0
Inoue introduced three families of surfaces, S0,S+ and S−, which are compact quotients
of
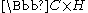(a product of a complexplane by a half-plane). These Inoue surfaces are
solvmanifold
Solvmanifold
In mathematics, a solvmanifold is a homogeneous space of a connected solvable Lie group. It may also be characterized as a quotient of a connected solvable Lie group by a closed subgroup...
s. They are obtained as quotients of
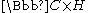by a solvable discretegroup which acts holomorphically on
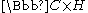.The solvmanifold surfaces constructed by Inoue all have second Betti number
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
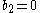. These surfaces are of Kodaira class VII,which means that they have
and Kodaira dimensionKodaira dimension
In algebraic geometry, the Kodaira dimension κ measures the size of the canonical model of a projective variety V.The definition of Kodaira dimension, named for Kunihiko Kodaira, and the notation κ were introduced in the seminar.-The plurigenera:...
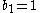. It was proven by BogomolovFedor Bogomolov
Fedor Alekseyevich Bogomolov is a Russian and American mathematician, known for his research in algebraic geometry and number theory. Bogomolov worked at Steklov Institute in Moscow before he became a professor at Courant Institute...
, Li-Yau
Shing-Tung Yau
Shing-Tung Yau is a Chinese American mathematician working in differential geometry. He was born in Shantou, Guangdong Province, China into a family of scholars from Jiaoling, Guangdong Province....
and Teleman that any surface of class VII
with b2 = 0 is a Hopf surface
Hopf surface
In complex geometry, a Hopf surface is a compact complex surface obtainedas a quotient of the complex vector space C2 \ 0...
or an Inoue-type solvmanifold.
These surfaces have no meromorphic functions and no curves.
K. Hasegawa gives a list of all complex 2-dimensional solvmanifolds; these are complex torus
Complex torus
In mathematics, a complex torus is a particular kind of complex manifold M whose underlying smooth manifold is a torus in the usual sense...
, hyperelliptic surface
Hyperelliptic surface
In mathematics, a hyperelliptic surface, or bi-elliptic surface, is a surface with an elliptic fibration over an elliptic curve. Any such surface can be written as the quotient of a product of two elliptic curves by a finite abelian group....
, Kodaira surface
Kodaira surface
In mathematics, a Kodaira surface is a compact complex surface of Kodaira dimension 0 and odd first Betti number.These are never algebraic, though they have non-constant meromorphic functions...
and
Inoue surfaces S0, S+ and S−.
The Inoue surfaces are constructed explicitly as follows.
Inoue surfaces of type S0
Let φ be an integer 3 × 3 matrix, withtwo complex eigenvalues
and a real eigenvalue c, with
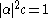.Then φ is invertible over integers, and defines an
action of the group
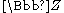of integers on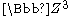. Let 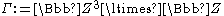.This group is a lattice in solvable
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
-
-
,
-
acting on
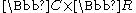, withthe
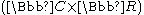-partacting by translations and the
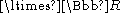-partas
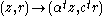.We extend this action to
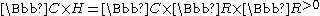
by setting
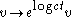,where t is the parameter of the
-part of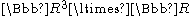,and acting trivially with the
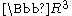
factor on
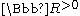. This actionis clearly holomorphic, and the quotient
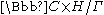is calledInoue surface of type S0.
The Inoue surface of type S0 is determined by the choice of an integer matrix φ, constrained as above. There is a countable number of such surfaces.
Inoue surfaces of type S+
Let n be a positive integer,and
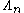be the group of uppertriangular matrices
where x, y, z are integers. Consider an
automorphism of
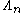, denoted as φ.The quotient of
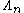byits center C is
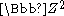.We assume that φ acts on
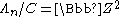
as a matrix with two positive real eigenvalues
a, b, and ab = 1.
Consider the solvable group
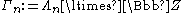,with
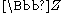acting on as φ. Identifying the group of upper triangular
matrices with
, we obtain anaction of
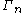on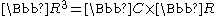.Define an action of
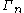on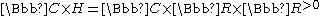with
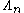acting trivially onthe
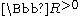-part and the 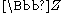acting as 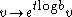.The same argument as for Inoue surfaces of type
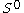
shows that this action is holomorphic. The
quotient
is called Inoue surface of type
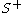.Inoue surfaces of type S−
Inoue surfaces of type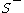are defined in the same was as for S+, but
two eigenvalues a, b of φ acting on
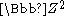
have opposite sign and satisfy ab = −1. Since a square of such an
endomorphism defines an Inoue surface of type S+,
an Inoue surface of type S− has an
unramified double cover of type S+.
Parabolic and hyperbolic Inoue surfaces
Parabolic and hyperbolic Inoue surfaces areKodaira class VII surfaces defined by Iku Nakamura
in 1984. They are not solvmanifolds.
These surfaces have positive second Betti number.
They have spherical shells, and can be deformed
into a blown-up Hopf surface
Hopf surface
In complex geometry, a Hopf surface is a compact complex surface obtainedas a quotient of the complex vector space C2 \ 0...
.
Parabolic Inoue surfaces are also known
as half-Inoue surfaces. These surfaces can be defined
as class VII0 (that is, class VII and
minimal
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
) surfaces with
an elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
and a cycle of rational curves.
Hyperbolic Inoue surfaces are class VII0
surfaces with two cycles of rational curves.