The instant centre of rotation, also called instantaneous centre and instant centre, is the point in a body undergoing planar movement that has zero velocity at a particular instant of time. At this instant the velocity vectors of the trajectories of other points in the body generate a circular field around this point, which is identical to what is generated by a pure rotation.

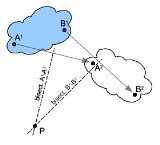
Planar movement of a body is often described using a plane figure moving in a two dimensional plane. The instant centre is the point in the moving plane around which all other points are rotating at a specific instant of time.

The continuous movement of a plane has an instant centre for every value of the time parameter. This generates a curve called the moving centrode

Centrode

Centrode in kinematics is the path traced by the instantaneous center of rotation of a rigid plane figure moving in a plane.-References:Homer D. Eckhardt Kinematic Design of Machines and Mechanisms, McGraw-Hill p. 63 ISBN 0070189536....

. The points in the fixed plane corresponding to these instant centres form the fixed centrode

Centrode

Centrode in kinematics is the path traced by the instantaneous center of rotation of a rigid plane figure moving in a plane.-References:Homer D. Eckhardt Kinematic Design of Machines and Mechanisms, McGraw-Hill p. 63 ISBN 0070189536....

.

Pole of a planar displacement

The instant centre can be considered the limiting case of the pole of a planar displacement.

The planar displacement of a body from position 1 to position 2 is defined by the combination of a planar rotation and planar translation

Translation (physics)

In physics, translation is movement that changes the position of an object, as opposed to rotation. For example, according to Whittaker:...

. For any planar displacement there is a point in the moving body that is in the same place before and after the displacement. This point is the pole of the planar displacement, and the displacement can be viewed as a rotation around this pole.

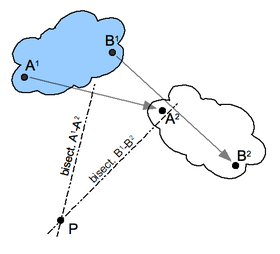
Construction for the pole of a planar displacement: First, select two points A and B in the moving body and locate the corresponding points in the two positions, see the illustration. In positions 1 and 2 these points define the segments A¹B¹, and A²B². Then, construct the perpendicular bisectors

Bisection

In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a bisector. The most often considered types of bisectors are the segment bisector and the angle bisector In geometry, bisection is the division of something into two equal...

 to the two segments A¹A² and B¹B². The intersection P of these two bisectors is the pole of the planar displacement. Notice that A¹ and A² lie on a circle around P. This is true for the corresponding positions of every point in the body.

If the two positions of a body are separated by an instant of time in a planar movement, then the pole of a displacement becomes the instant centre. In this case, the segments constructed between the instantaneous positions of point the points A and B, become the velocity vectors V_A and V_B. The lines perpendicular to these velocity vectors intersect in the instant centre.

Pure translation

If the displacement between two positions is a pure translation, then the perpendicular bisectors of the segments A¹B¹ and A²B² form parallel lines. These lines are considered to intersect at a point on the line at infinity

Line at infinity

In geometry and topology, the line at infinity is a line that is added to the real plane in order to give closure to, and remove the exceptional cases from, the incidence properties of the resulting projective plane. The line at infinity is also called the ideal line.-Geometric formulation:In...

, thus the pole of this planar displacement is said to "lie at infinity" in the direction of the perpendicular bisectors.

In the limit, pure translation becomes planar movement with point velocity vectors that are parallel. In this case, the instant centre is said to lie at infinity in the direction perpendicular to the velocity vectors.

Instant centre of a wheel rolling without slipping

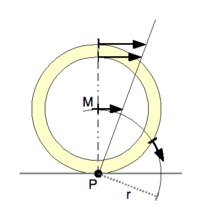
Consider the planar movement of a circular wheel rolling without slipping on a linear road, see sketch 3. The wheel rotates around its axis M, which translates in a direction parallel to the road. The point of contact P of the wheel with road does not slip, which means the point P has zero velocity. Thus, at the instant the point P on the wheel comes in contact with the road it becomes an instant centre.

The set of points of the moving wheel that become instant centres is the circle itself, which defines the moving centrode. The points in the fixed plane that correspond to these instant centres is the line of the road, which defines the fixed centrode.

The velocity vector of a point A in the wheel is perpendicular to the segment AP and is proportional to the length of this segment. In particular, the velocities of points in the wheel are determined by the angular velocity of the wheel in rotation around P. The velocity vectors of a number of points are illustrated in sketch 3.

The further a point in the wheel is from the instant centre P, the proportionally larger its speed. Therefore, the point at the top of the wheel moves in the same direction as the centre M of the wheel, but twice as fast, since it is twice the distance away from P. All points that are a distance equal to the radius of the wheel 'r' from point P move at the same speed as the point M but in different directions. This is shown for a point on the wheel that has the same speed as M but moves in the direction tangent to the circle around P.

Instant centre of rotation and mechanisms

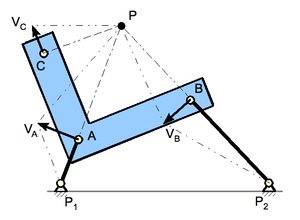
Sketch 1 above shows a four-bar linkage where a number of instant centres of rotation are illustrated. The rigid body noted by the letters BAC is connected with links P₁-A and P₂-B to a base or frame.

The three moving parts of this mechanism (the base is not moving) are: link P₁-A, link P₂-B, and body BAC. For each of these three parts an instant centre of rotation may be determined.

Considering first link P₁-A: all points on this link, including point A, rotate around point P₁. Since P₁ is the only point not moving in the given plane it may be called the instant centre of rotation for this link. Point A, at distance P₁-A from P₁, moves in a circular motion in a direction perpendicular to the link P₁-A, as indicated by vector V_A.

The same applies to link P₂-B: point P₂ is the instant centre of rotation for this link and point B moves in the direction as indicated by vector V_B.

For determining the instant centre of rotation of the third element of the linkage, the body BAC, the two points A and B are used because its moving characteristics are known, as derived from the information about the links P₁-A and P₂-B.

The direction of speed of point A is indicated by vector V_A. Its instant centre of rotation must be perpendicular to this vector (as V_A is tangentially located on the circumference of a circle). The only line that fills the requirement is a line colinear with link P₁-A. Somewhere on this line there is a point P, the instant centre of rotation for the body BAC.
What applies to point A also applies to point B, therefore this instant centre of rotation P is located on a line perpendicular to vector V_B, a line colinear with link P₂-B. Therefore, the instant centre of rotation P of body BAC is the point where the lines through P₁-A and P₂-B cross.

Since this instant centre of rotation P is the centre for all points on the body BAC for any random point, say point C, the speed and direction of movement may be determined: connect P to C. The direction of movement of point C is perpendicular to this connection. The speed is proportional to the distance to point P.

Continuing this approach with the two links P₁-A and P₂-B rotating around their own instant centres of rotation the centrode for instant centre of rotation P may be determined. From this the path of movement for C or any other point on body BAC may be determined.

Examples of application

In biomechanical research the instant centre of rotation is observed for the functioning of the joints in the upper and lower extremities.
For example in analysing the knee

Knee

The knee joint joins the thigh with the leg and consists of two articulations: one between the fibula and tibia, and one between the femur and patella. It is the largest joint in the human body and is very complicated. The knee is a mobile trocho-ginglymus , which permits flexion and extension as...

,
ankle

Ankle

The ankle joint is formed where the foot and the leg meet. The ankle, or talocrural joint, is a synovial hinge joint that connects the distal ends of the tibia and fibula in the lower limb with the proximal end of the talus bone in the foot...

, or shoulder

Shoulder

The human shoulder is made up of three bones: the clavicle , the scapula , and the humerus as well as associated muscles, ligaments and tendons. The articulations between the bones of the shoulder make up the shoulder joints. The major joint of the shoulder is the glenohumeral joint, which...

 joints.
Such knowledge assists in developing artificial joints and prosthesis

Prosthesis

In medicine, a prosthesis, prosthetic, or prosthetic limb is an artificial device extension that replaces a missing body part. It is part of the field of biomechatronics, the science of using mechanical devices with human muscle, skeleton, and nervous systems to assist or enhance motor control...

, such as elbow or finger joints.

Study of the joints of horses: "...velocity vectors determined from the instant centers of rotation indicated that the joint surfaces slide on each other.".

Studies on turning a vessel moving through water.

The braking

Brake

A brake is a mechanical device which inhibits motion. Its opposite component is a clutch. The rest of this article is dedicated to various types of vehicular brakes....

 characteristiscs of a car may be improved by varying the design of a brake pedal mechanism.

Designing the suspension of a bicycle, or of a car.

In the case of the coupler link in a four-bar linkage, such as a double wishbone suspension

Double wishbone suspension

In automobiles, a double wishbone suspension is an independent suspension design using two wishbone-shaped arms to locate the wheel. Each wishbone or arm has two mounting points to the chassis and one joint at the knuckle. The shock absorber and coil spring mount to the wishbones to control...

 in front view, the perpendiculars to the velocity lie along the links joining the grounded link to the coupler link. This construction is used to establish the kinematic Roll center

Roll center

The roll center of a vehicle is the notional point at which the cornering forces in the suspension are reacted to the vehicle body.-Theory:There are two definitions of roll center...

 of the suspension.

See also

• Roll center
  Roll center
  The roll center of a vehicle is the notional point at which the cornering forces in the suspension are reacted to the vehicle body.-Theory:There are two definitions of roll center...
  
  
• Screw axis
  Screw axis
  The screw axis of an object is a line that is simultaneously the axis of rotation and the line along which a translation occurs...
  
  
• Rigid body
  Rigid body
  In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
  
  
• Rotation around a fixed axis
  Rotation around a fixed axis
  Rotation around a fixed axis is a special case of rotational motion. The fixed axis hypothesis exclude the possibility of a moving axis, and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation around more than one axis at the same...
  
  
• Angular velocity
  Angular velocity
  In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...