Inverse transform sampling method
Encyclopedia
Inverse transform sampling, also known as the inverse probability integral transform or inverse transformation method or Smirnov transform or even golden rule, is a basic method for pseudo-random number sampling
, i.e. for generating sample numbers at random from any probability distribution
given its cumulative distribution function
(cdf). Subject to the restriction that the distribution is continuous, this method is generally applicable (and can be computationally efficient if the cdf can be analytically inverted
), but may be too computationally expensive in practice for some probability distributions. The Box–Muller transform is an example of an algorithm that is specific to generating samples from a normal distribution, but is more computationally efficient. It is often the case that, even for simple distributions, the inverse transform sampling method can be improved on: see, for example, the ziggurat algorithm
and rejection sampling
.
states that if
is a continuous random variable with cumulative distribution function
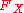, then the random variable 
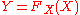has a uniform distribution
on [0, 1]. The inverse probability integral transform is just the inverse of this: specifically, if
has a uniform distribution on [0, 1] and if 
has a cumulative distribution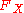 
, then the cumulative distribution function of the random variable 
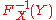is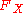 
.
The inverse transform sampling method works as follows:
Expressed differently, given a continuous uniform variable U in [0, 1] and an invertible
cumulative distribution function F, the random variable X = F −1(U) has distribution F (or, X is distributed F).
A treatment of such inverse functions as objects satisfying differential equations can be given. Some such differential equations admit explicit power series solutions, despite their non-linearity.
, and let F−1 be its inverse function (using the infimum
because CDFs are weakly monotonic and right-continuous
):
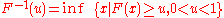
Claim: If U is a uniform
random variable on (0, 1) then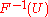
follows the distribution F.
Proof:
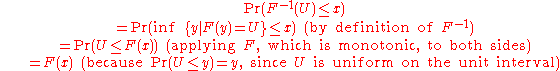
Pseudo-random number sampling
Pseudo-random number sampling or non-uniform pseudo-random variate generation is the numerical practice of generating pseudo-random numbers that are distributed according to a given probability distribution....
, i.e. for generating sample numbers at random from any probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
given its cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
(cdf). Subject to the restriction that the distribution is continuous, this method is generally applicable (and can be computationally efficient if the cdf can be analytically inverted
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
), but may be too computationally expensive in practice for some probability distributions. The Box–Muller transform is an example of an algorithm that is specific to generating samples from a normal distribution, but is more computationally efficient. It is often the case that, even for simple distributions, the inverse transform sampling method can be improved on: see, for example, the ziggurat algorithm
Ziggurat algorithm
The ziggurat algorithm is an algorithm for pseudo-random number sampling. Belonging to the class of rejection sampling algorithms, it relies on an underlying source of uniformly-distributed random numbers, typically from a pseudo-random number generator, as well as precomputed tables. The...
and rejection sampling
Rejection sampling
In mathematics, rejection sampling is a basic pseudo-random number sampling technique used to generate observations from a distribution. It is also commonly called the acceptance-rejection method or "accept-reject algorithm"....
.
Definition
The probability integral transformProbability integral transform
In statistics, the probability integral transform or transformation relates to the result that data values that are modelled as being random variables from any given continuous distribution can be converted to random variables having a uniform distribution...
states that if
is a continuous random variable with cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
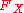, then the random variable 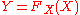has a uniform distributionUniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
on [0, 1]. The inverse probability integral transform is just the inverse of this: specifically, if
has a uniform distribution on [0, 1] and if has a cumulative distribution 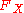, then the cumulative distribution function of the random variable 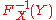is 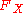.The method
The problem that the inverse transform sampling method solves is as follows:- Let X be a random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
whose distribution can be described by the cumulative distribution functionCumulative distribution functionIn probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
F. - We want to generate values of X which are distributed according to this distribution.
The inverse transform sampling method works as follows:
- Generate a random numberPseudorandom number generatorA pseudorandom number generator , also known as a deterministic random bit generator , is an algorithm for generating a sequence of numbers that approximates the properties of random numbers...
u from the standard uniform distribution in the interval [0,1]. - Compute the value x such that F(x) = u.
- Take x to be the random number drawn from the distribution described by F.
Expressed differently, given a continuous uniform variable U in [0, 1] and an invertible
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
cumulative distribution function F, the random variable X = F −1(U) has distribution F (or, X is distributed F).
A treatment of such inverse functions as objects satisfying differential equations can be given. Some such differential equations admit explicit power series solutions, despite their non-linearity.
Proof of correctness
Let F be a continuous cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
, and let F−1 be its inverse function (using the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
because CDFs are weakly monotonic and right-continuous
Càdlàg
In mathematics, a càdlàg , RCLL , or corlol function is a function defined on the real numbers that is everywhere right-continuous and has left limits everywhere...
):
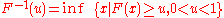
Claim: If U is a uniform
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
random variable on (0, 1) then
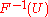follows the distribution F.Proof:
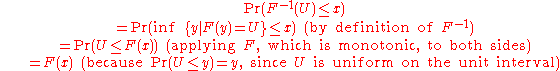
See also
- Probability integral transformProbability integral transformIn statistics, the probability integral transform or transformation relates to the result that data values that are modelled as being random variables from any given continuous distribution can be converted to random variables having a uniform distribution...
- CopulaCopula (statistics)In probability theory and statistics, a copula can be used to describe the dependence between random variables. Copulas derive their name from linguistics....
, defined by means of probability integral transform. - Quantile functionQuantile functionIn probability and statistics, the quantile function of the probability distribution of a random variable specifies, for a given probability, the value which the random variable will be at, or below, with that probability...
, for the explicit construction of inverse CDFs. - Inverse distribution function for a precise mathematical definition for distributions with discrete components.