
Josip Plemelj
Encyclopedia
Josip Plemelj was a Slovene mathematician
, whose main contributions were to the theory of analytic functions and the application of integral equations to potential theory
.
near Bled Castle
in Austria-Hungary
(now Slovenia
); he died in Ljubljana
, Yugoslavia
(now Slovenia). His father, Urban, a carpenter
and crofter
, died when Josip was only a year old. His mother Marija, née Mrak, found bringing up the family alone very hard, but she was able to send her son to school in Ljubljana where Plemelj studied from 1886 to 1894. After leaving and obtaining the necessary examination results he went to Vienna
in 1894 where he had applied to Faculty of Arts to study mathematics
, physics
and astronomy
. His professors in Vienna were von Escherich for mathematical analysis
, Gegenbauer and Mertens
for arithmetic
and algebra
, Weiss
for astronomy, Stefan
's student Boltzmann
for physics.
On May 1898 Plemelj presented his doctoral
thesis under Escherich's tutelage entitled O linearnih homogenih diferencialnih enačbah z enolično periodičnimi koeficienti (Über lineare homogene Differentialgleichungen mit eindeutigen periodischen Koeffizienten, About linear homogeneous differential equations with uniform periodical coefficients). He continued with his study in Berlin
(1899/1900) under the German mathematicians Frobenius
and Fuchs and in Göttingen
(1900/1901) under Klein
and Hilbert
.
In April 1902 he became a private senior lecturer at the University of Vienna
. In 1906 he was appointed assistant at the Technical University of Vienna. In 1907 he became associate professor and in 1908 full professor of mathematics at the University of Chernivtsi (Russian
Черновцы), Ukraine
. From 1912 to 1913 he was dean of this faculty. In 1917 his political views led him to be forcibly ejected by the Government and he fled to Bohemia
(Moravska). After the First World War
he became a member of the University Commission under the Slovene Provincial Government and helped establish the first Slovene university at Ljubljana, and was elected its first rector. In the same year he was appointed professor of mathematics at the Faculty of Arts. After the Second World War he joined the Faculty of Natural Science and Technology (FNT). He retired in 1957 after having lectured in mathematics for 40 years.
s, potential theory
, the theory of analytic function
s, and functional analysis
. Plemelj encountered integral equations while still a student at Göttingen, when the Swedish professor Erik Holmgren
gave a lecture on the work of his fellow countryman Fredholm
on linear integral equations of the 1st and 2nd kind. Spurred on by Hilbert, Göttingen mathematicians attacked this new area of research and Plemelj was one of the first to publish original results on the question, applying the theory of integral equations to the study of harmonic functions in potential theory.
His most important work in potential theory is summarised in his 1911 book Researches in Potential Theory (Potentialtheoretische Untersuchungen), which received the Jablonowski Society award in Leipzig (1500 marks), and the Richard Lieben award from the University of Vienna (2000 crowns) for the most outstanding work in the field of pure and applied mathematics written by any kind of 'Austrian' mathematician in the previous three years.
His most original contribution is the elementary solution he provided for the Riemann–Hilbert problem f+=g f− about the existence of a differential equation with given monodromy group. The solution, published in his 1908 article "Riemannian classes of functions with given monodromy group", rests on three formulas that now carry his name, which connect the values taken by a holomorphic function
at the boundary of an arc :
:
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
, whose main contributions were to the theory of analytic functions and the application of integral equations to potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
.
Life
Plemelj was born in the village of BledBled
Bled is a municipality in northwestern Slovenia in the region of Upper Carniola. The area, within the Julian Alps, is a popular tourist destination.-History:...
near Bled Castle
Bled Castle
Bled Castle is a medieval castle built on a precipice above the city of Bled in Slovenia, overlooking Lake Bled. According to written sources, it is the oldest Slovenian castle and is currently one of the most visited tourist attractions in Slovenia....
in Austria-Hungary
Austria-Hungary
Austria-Hungary , more formally known as the Kingdoms and Lands Represented in the Imperial Council and the Lands of the Holy Hungarian Crown of Saint Stephen, was a constitutional monarchic union between the crowns of the Austrian Empire and the Kingdom of Hungary in...
(now Slovenia
Slovenia
Slovenia , officially the Republic of Slovenia , is a country in Central and Southeastern Europe touching the Alps and bordering the Mediterranean. Slovenia borders Italy to the west, Croatia to the south and east, Hungary to the northeast, and Austria to the north, and also has a small portion of...
); he died in Ljubljana
Ljubljana
Ljubljana is the capital of Slovenia and its largest city. It is the centre of the City Municipality of Ljubljana. It is located in the centre of the country in the Ljubljana Basin, and is a mid-sized city of some 270,000 inhabitants...
, Yugoslavia
Socialist Federal Republic of Yugoslavia
The Socialist Federal Republic of Yugoslavia was the Yugoslav state that existed from the abolition of the Yugoslav monarchy until it was dissolved in 1992 amid the Yugoslav Wars. It was a socialist state and a federation made up of six socialist republics: Bosnia and Herzegovina, Croatia,...
(now Slovenia). His father, Urban, a carpenter
Carpenter
A carpenter is a skilled craftsperson who works with timber to construct, install and maintain buildings, furniture, and other objects. The work, known as carpentry, may involve manual labor and work outdoors....
and crofter
Croft (land)
A croft is a fenced or enclosed area of land, usually small and arable with a crofter's dwelling thereon. A crofter is one who has tenure and use of the land, typically as a tenant farmer.- Etymology :...
, died when Josip was only a year old. His mother Marija, née Mrak, found bringing up the family alone very hard, but she was able to send her son to school in Ljubljana where Plemelj studied from 1886 to 1894. After leaving and obtaining the necessary examination results he went to Vienna
Vienna
Vienna is the capital and largest city of the Republic of Austria and one of the nine states of Austria. Vienna is Austria's primary city, with a population of about 1.723 million , and is by far the largest city in Austria, as well as its cultural, economic, and political centre...
in 1894 where he had applied to Faculty of Arts to study mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
. His professors in Vienna were von Escherich for mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, Gegenbauer and Mertens
Franz Mertens
Franz Mertens was a German mathematician. He was born in Środa in the Grand Duchy of Poznań, Kingdom of Prussia and died in Vienna, Austria....
for arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
and algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, Weiss
Edmund Weiss
Edmund Weiß was an Austrian astronomer.He was born in Frývaldov, Austrian Silesia, now Jeseník, Czech Silesia. In 1869 he became a professor at the University of Vienna. He was named the director of the Vienna observatory in 1878...
for astronomy, Stefan
Joseph Stefan
Joseph Stefan was a physicist, mathematician, and poet of Slovene mother tongue and Austrian citizenship.- Life and work :...
's student Boltzmann
Ludwig Boltzmann
Ludwig Eduard Boltzmann was an Austrian physicist famous for his founding contributions in the fields of statistical mechanics and statistical thermodynamics...
for physics.
On May 1898 Plemelj presented his doctoral
Doctor of Philosophy
Doctor of Philosophy, abbreviated as Ph.D., PhD, D.Phil., or DPhil , in English-speaking countries, is a postgraduate academic degree awarded by universities...
thesis under Escherich's tutelage entitled O linearnih homogenih diferencialnih enačbah z enolično periodičnimi koeficienti (Über lineare homogene Differentialgleichungen mit eindeutigen periodischen Koeffizienten, About linear homogeneous differential equations with uniform periodical coefficients). He continued with his study in Berlin
Berlin
Berlin is the capital city of Germany and is one of the 16 states of Germany. With a population of 3.45 million people, Berlin is Germany's largest city. It is the second most populous city proper and the seventh most populous urban area in the European Union...
(1899/1900) under the German mathematicians Frobenius
Ferdinand Georg Frobenius
Ferdinand Georg Frobenius was a German mathematician, best known for his contributions to the theory of differential equations and to group theory...
and Fuchs and in Göttingen
Göttingen
Göttingen is a university town in Lower Saxony, Germany. It is the capital of the district of Göttingen. The Leine river runs through the town. In 2006 the population was 129,686.-General information:...
(1900/1901) under Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
and Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
.
In April 1902 he became a private senior lecturer at the University of Vienna
University of Vienna
The University of Vienna is a public university located in Vienna, Austria. It was founded by Duke Rudolph IV in 1365 and is the oldest university in the German-speaking world...
. In 1906 he was appointed assistant at the Technical University of Vienna. In 1907 he became associate professor and in 1908 full professor of mathematics at the University of Chernivtsi (Russian
Russian language
Russian is a Slavic language used primarily in Russia, Belarus, Uzbekistan, Kazakhstan, Tajikistan and Kyrgyzstan. It is an unofficial but widely spoken language in Ukraine, Moldova, Latvia, Turkmenistan and Estonia and, to a lesser extent, the other countries that were once constituent republics...
Черновцы), Ukraine
Ukraine
Ukraine is a country in Eastern Europe. It has an area of 603,628 km², making it the second largest contiguous country on the European continent, after Russia...
. From 1912 to 1913 he was dean of this faculty. In 1917 his political views led him to be forcibly ejected by the Government and he fled to Bohemia
Bohemia
Bohemia is a historical region in central Europe, occupying the western two-thirds of the traditional Czech Lands. It is located in the contemporary Czech Republic with its capital in Prague...
(Moravska). After the First World War
World War I
World War I , which was predominantly called the World War or the Great War from its occurrence until 1939, and the First World War or World War I thereafter, was a major war centred in Europe that began on 28 July 1914 and lasted until 11 November 1918...
he became a member of the University Commission under the Slovene Provincial Government and helped establish the first Slovene university at Ljubljana, and was elected its first rector. In the same year he was appointed professor of mathematics at the Faculty of Arts. After the Second World War he joined the Faculty of Natural Science and Technology (FNT). He retired in 1957 after having lectured in mathematics for 40 years.
Research
Plemelj's main research interests were the theory of linear differential equations, integral equationIntegral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
s, potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
, the theory of analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s, and functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
. Plemelj encountered integral equations while still a student at Göttingen, when the Swedish professor Erik Holmgren
Erik Holmgren
Erik Holmgren is a retired football defender.During his club career, Holmgren played for HJK Helsinki, GAIS, FinnPa, Pallokerho-35 and FC Jokerit. He made 60 appearances for the Finland national team, scoring 2 goals....
gave a lecture on the work of his fellow countryman Fredholm
Erik Ivar Fredholm
Erik Ivar Fredholm was a Swedish mathematician who established the modern theory of integral equations. His 1903 paper in Acta Mathematica is considered to be one of the major landmarks in the establishment of operator theory.The lunar crater Fredholm is named after him.-List of publications:* E.I...
on linear integral equations of the 1st and 2nd kind. Spurred on by Hilbert, Göttingen mathematicians attacked this new area of research and Plemelj was one of the first to publish original results on the question, applying the theory of integral equations to the study of harmonic functions in potential theory.
His most important work in potential theory is summarised in his 1911 book Researches in Potential Theory (Potentialtheoretische Untersuchungen), which received the Jablonowski Society award in Leipzig (1500 marks), and the Richard Lieben award from the University of Vienna (2000 crowns) for the most outstanding work in the field of pure and applied mathematics written by any kind of 'Austrian' mathematician in the previous three years.
His most original contribution is the elementary solution he provided for the Riemann–Hilbert problem f+=g f− about the existence of a differential equation with given monodromy group. The solution, published in his 1908 article "Riemannian classes of functions with given monodromy group", rests on three formulas that now carry his name, which connect the values taken by a holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
at the boundary of an arc
 :
:-
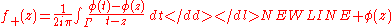
-

-
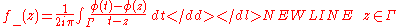
These formulae are variously called the Plemelj formulae, the Sokhatsky–Weierstrass theorem, the Sokhotsky-Plemelj formulae, or sometimes (mainly in German literature) the Plemelj-Sokhotsky formulae, after the Russian mathematician SokhotskyYulian Vasilievich SokhotskiJulian Karol Sochocki was a Polish mathematician....
(Юлиан Карл Васильевич Сохоцкий) (1842–1927).
From his methods on solving the Riemann problem had developed the theory of singular integral equations (MSC (2000) 45-Exx) which was entertained above all by the Russian school at the head of Muskhelishvili (Николай Иванович Мусхелищвили) (1891–1976).
Also important are Plemelj's contributions to the theory of analytic functions in solving the problem of uniformization of algebraic functionAlgebraic functionIn mathematics, an algebraic function is informally a function that satisfies a polynomial equation whose coefficients are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equationwhere the coefficients ai are polynomial...
s, contributions on formulation of the theorem of analytic extension of designDesignDesign as a noun informally refers to a plan or convention for the construction of an object or a system while “to design” refers to making this plan...
s and treatises in algebraAlgebraAlgebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
and in number theoryNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
.
1912 Plemelj published a very simple proof for the Fermat's last theoremFermat's Last TheoremIn number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
for exponent n = 5, which was first given almost simultaneously by DirichletJohann Peter Gustav Lejeune DirichletJohann Peter Gustav Lejeune Dirichlet was a German mathematician with deep contributions to number theory , as well as to the theory of Fourier series and other topics in mathematical analysis; he is credited with being one of the first mathematicians to give the modern formal definition of a...
in 1828 and LegendreAdrien-Marie LegendreAdrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
in 1830. Their proofs difficult, while Plemelj showed how to use the ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
we get if we extend the rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s by √ 5.
His arrival in Ljubljana 1919 was very important for development of mathematics in Slovenia. As a good teacher he had raised several generations of mathematicians and engineers. His most famous student is Ivan VidavIvan VidavIvan Vidav is a Slovenian mathematician.Ivan Vidav was born in Opčine near Trieste , Italy. He is Josip Plemelj's student. Vidav got his Ph.D...
. After the 2nd World War Slovenska akademija znanosti in umetnosti (Slovene Academy of Sciences and Arts) (SAZU) had published his three year's course of lectures for students of mathematics: Teorija analitičnih funkcij (The theory of analytic functions),
(SAZU, Ljubljana 1953, pp XVI+516), Diferencialne in integralske enačbe. Teorija in uporaba (Differential and integral equations. The theory and the application).
Plemelj found a formula for a sumSUMSUM can refer to:* The State University of Management* Soccer United Marketing* Society for the Establishment of Useful Manufactures* StartUp-Manager* Software User’s Manual,as from DOD-STD-2 167A, and MIL-STD-498...
of normal derivatives of one layered potential in the internal or external region. He was pleased also with algebra and number theory, but he had published only few contributions from these fields — for example a book entitled Algebra in teorija števil (Algebra and the number theory) (SAZU, Ljubljana 1962, pp XIV+278) which was published abroad as his last work Problemi v smislu Riemanna in Kleina (Problems in the Sense of Riemann and Klein) (edition and translation by J. R. M. Radok, "Interscience Tract in Pure and Applied Mathematics", No. 16, Interscience Publishers: John Wiley & SonsJohn Wiley & SonsJohn Wiley & Sons, Inc., also referred to as Wiley, is a global publishing company that specializes in academic publishing and markets its products to professionals and consumers, students and instructors in higher education, and researchers and practitioners in scientific, technical, medical, and...
, New YorkNew YorkNew York is a state in the Northeastern region of the United States. It is the nation's third most populous state. New York is bordered by New Jersey and Pennsylvania to the south, and by Connecticut, Massachusetts and Vermont to the east...
, LondonLondonLondon is the capital city of :England and the :United Kingdom, the largest metropolitan area in the United Kingdom, and the largest urban zone in the European Union by most measures. Located on the River Thames, London has been a major settlement for two millennia, its history going back to its...
, SydneySydneySydney is the most populous city in Australia and the state capital of New South Wales. Sydney is located on Australia's south-east coast of the Tasman Sea. As of June 2010, the greater metropolitan area had an approximate population of 4.6 million people...
1964, pp VII+175). This work deals with questions which were of his most interests and examinations. His bibliography includes 33 units, from which 30 are scientific treatises and had been published among the others in a magazines such as: "Monatshefte für Mathematik und Physik", "Sitzungsberichte der kaiserlichen Akademie der Wissenschaften"; in Wien, "Jahresbericht der deutschen Mathematikervereinigung", "Gesellschaft deutscher Naturforscher und Ärzte" in Verhandlungen, "Bulletin des Sciences Mathematiques", "Obzornik za matematiko in fiziko" and "Publications mathematiques de l'Universite de Belgrade". When French mathematician Charles Émile PicardCharles Émile PicardCharles Émile Picard FRS was a French mathematician. He was elected the fifteenth member to occupy seat 1 of the Académie Française in 1924.- Biography :...
denoted Plemelj's works as "deux excellents memoires", Plemelj became known in mathematical world.
Plemelj was regular member of the SAZU since its foundation in 1938, corresponding member of the JAZU (Yugoslav Academy of Sciences and Arts) in Zagreb, Croatia since 1923, corresponding member of the SANU (Serbian Academy of Sciences and Arts) in Belgrade since 1930 (1931). 1954 he received the highest award for research in Slovenia the Prešeren award. The same year he was elected for corresponding member of Bavarian Academy of Sciences in Munich.
1963 for his 90th anniversary University of LjubljanaUniversity of LjubljanaThe University of Ljubljana is the oldest and largest university in Slovenia. With 64,000 enrolled graduate and postgraduate students, it is among the largest universities in Europe.-Beginnings:...
granted him title of the honorary doctor. Plemelj was first teacher of mathematics at Slovene university and 1949 became first honorary member of ZDMFAJ, (Yugoslav Union of societies of mathematicians, physicists and astronomers). He left his villa in BledBledBled is a municipality in northwestern Slovenia in the region of Upper Carniola. The area, within the Julian Alps, is a popular tourist destination.-History:...
to the DMFASociety of Mathematicians, Physicists and Astronomers of SloveniaThe Society of Mathematicians, Physicists and Astronomers of Slovenia is the main Slovene society in the field of mathematics, physics and astronomy....
where today is his memorial room.
Plemelj did not do extra preparation for lectures; he didn't have any notes. He used to say that he thought over the lecture subject on the way from his home in Gradišče to the University. Students are said to have got the impression that he was creating teaching material on the spot and that they were witnessing the formation of something new. He was writing formulae on the table beautifully although they were composited from Greek, Latin or Gothic letters. He requested the same from students. They had to write distinct.
Plemelj is said to have had very refined ear for language and he had made a solid base for the development of the Slovene mathematical terminology. He had accustomed students for a fine language and above all for a clear and logical phraseology. For example, he would become angry if they used the word 'rabiti' (to use) instead of the word 'potrebovati' (to need). For this reason he said: "The engineer who does not know mathematics never needs it. But if he knows it, he uses it frequently".
A geometrical construction from his schooldays
Plemelj had shown his great gift for mathematics early in elementary school. He mastered the whole of the high school syllabus by the beginning of the fourth year and began to tutor students for their graduation examinations. At that time he discovered alone seriesSeries (mathematics)A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
for sinSineIn mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
x and cos x. Actually he found a series for cyclometric function arccos x and after that he just inverted this series and then guessed a principle for coefficients. Yet he did not have a proof for that.
Plemelj had great joy for a difficult constructional tasks from geometry. From his high school days originates an elementary problem — his later construction of regular sevenfold polygon inscribed in a circle otherwise exactly and not approximately with simple solution as an angle trisectionAngle trisectionAngle trisection is a classic problem of compass and straightedge constructions of ancient Greek mathematics. It concerns construction of an angle equal to one-third of a given arbitrary angle, using only two tools: an un-marked straightedge, and a compass....
which was yet not known in those days and which necessarily leads to the old Indian or Babylonian approximate construction. He started to occupy himself with mathematics in fourth and fifth class of high school. Beside in mathematics he was interested also in natural science and especially astronomy. He studied celestial mechanics already at high school. He liked observing the starStarA star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
s. His eyesight was so sharp he could see the planetPlanetA planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
VenusVenusVenus is the second planet from the Sun, orbiting it every 224.7 Earth days. The planet is named after Venus, the Roman goddess of love and beauty. After the Moon, it is the brightest natural object in the night sky, reaching an apparent magnitude of −4.6, bright enough to cast shadows...
even in the daytime.
Let us hear about his early days in school in his own words: "It was the April 1891 in fifth class. The class had two rows of desks with crossing in between and I was sitting on the most side inside chair very rear. I think there were only two desks after me. Professor Borštner did not lecture. He had only given a lection from the book for the next lesson. He called to the blackboard two pupils and there he was discussing the subject and furthermore with this he included the whole class for cooperation. He used to have such a habit gratefully to give geometrical constructional tasks which he dictated from some collection he brought with. Once he gave amongst the other a task: Draught a triangle if one side, its altitude and a difference of two angles along it are given. Classmates had appealed to me before the lesson if the task was a little bit hard. They could not solve this task after several lessons and he had asked them the other. Borštner used to come from before the master's desk and he stopped ahead of me, sat toward me in the desk and hence he examined. After sometime he had said we should solve that task. Perhaps he was suspicious about that we had not yet solved it so he turned to me and asked me if I had tried this construction. I had said to him I could not find any path for the solution. Then he said he would show it in the next lesson. This had plucked up my courage to inspect it again. I had found a solution with subsidiary points, lines and so forth which seems to be inaccessible for human mind if the way which had inevitably led me to my aim is hidden from. Next lesson professor Borštner had sat toward me in the desk again. After customary examination of my classmates he said: "Well, let us work out that construction task." I whispered him I had succeeded till then and he said: "So, let me show how had you done this." He thought I would show him written on paper and he said: "Well, all-right." He had stepped aside and we went before the blackboard. I drew a triangle ΔABC with an ordinary analysis: Given side AB = c, its altitude vc and the difference 0 < α − β < π.
Let us draw a perpendicular AA' from A to side AB and let AA' = 2 vc. Let us bind A' with C in the way to be A'C = AC = b and draw A'B = m. Along the side
A'C let us gather out along A' an angle α and on the left side of a triangle A'B' = c. On this way the risen triangle is ΔA'B'C ~ ΔABC. By B lies an angle <A'B'C = β and an angle <A'CB' = γ.
A triangle ΔBCB' is isosceles and <BCB' = 2 α, so we have < BB'C = π/2 − α. Now it is the angle <A'B'B = π/2 − α + β and we can construct over the side BA' a circumferential angle of a certain circle. We get a point B' at once because it is A'B' = c. Because a triangle ΔBCB' is isosceles a point C lies on a symmetric of the side BB' where it intersects a parallel with AB in a given altitude vc. With this the triangle ΔABC is drawn. Professor Borštner was gazing when he saw this curious solution and he held of his head: "Aber um Hergottswillen, das ist doch harsträubend, das ist doch doch menschenunmöglich auf so einen Einfall zu kommen; sagen Sie mir doch, was hat Sie zu dieser Idee geführt!" I said to him I had not guessed this strange solution but I had asked myself about a trigonometric determination of a triangle because I could not find the solution in the other way. Geometric interpretation of this solution had led me up to this pure geometrically understandable construction. We did not spoke anymore about this with professor Borštner, but he had after that shown another easier solution, which I could imitate from my own construction and which I had not perceived because I had precisely traced way.
Trigonometric solution is easy: with altitude vc from point C to side AB it breaks in two parts vc cot α and vc cot β.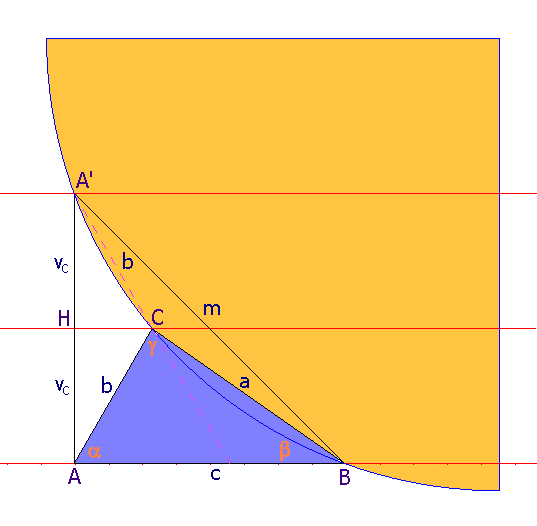
Then we have:
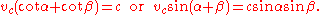
We can then write:
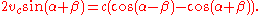
Because α + β = π − γ, this equation is:
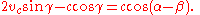
From this equation we have to obtain an angle γ. The easiest way is if we introduce a certain subsidiary angle μ. Namely we raise:
- 2 vc = m cos μ c = m sin μ.
Both equations give us for μ a uniform certain acute angle and for m a certain positive length. The equation for γ is then:
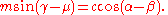
We can consider this equation as a theorem of the sine for a certain triangle in which c and m are its sides and their opposite angles are γ − μ and π/2 ± (α − β) respectively ( lightgreen triangle on the picture below ). In this quoted construction this triangle is ΔBA'B', where BA' = m and A'B' = c, the angle <BB'A' = π/2 − α + α and the angle <A'BB' = γ − μ, as we can easily see. In my construction this requested triangle is drafted twice. I saw later on we can interpret above equation with a triangle which has a side AB already. This leads us to very beautiful and short construction. Requested triangle is ΔK'AB.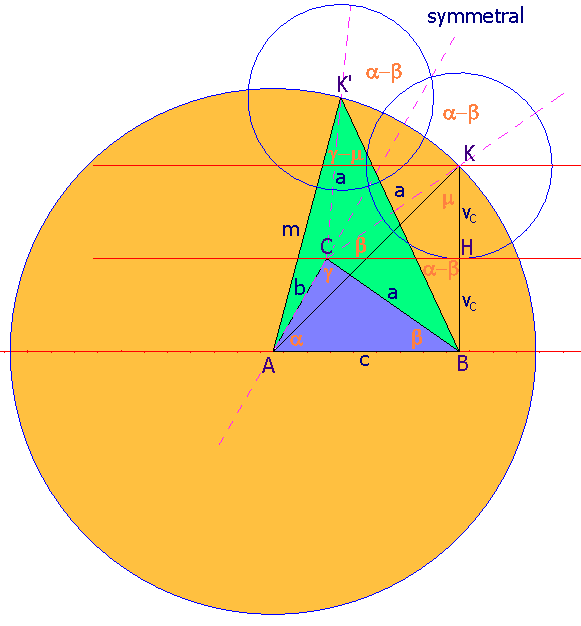
Straight line CK = a is symmetrically displaced in CK' = a and at the same time is AK = AK' = m. I had spoken as a professor in Černovice with two of my students about this elementary geometrical problem and I said that my high school teacher had dictated this task from a certain collection. They brought me a collection indeed where there was the exact picture from Borštner's construction. Unfortunately I had not written down a title of that book which was with no doubt professor Borštner's collection. Our teacher's library at classical gymnasium in Ljubljana does not have this book at present. But I got from there a Wiegand's book entitled Geometrijske naloge za višje gimnazije (Geometrische Aufgaben für Obergymnasien, Geometric exercises for upper gymnasiums), which does not have this exercise. I found in it a task: construct a triangle if we know one length of an angle symmetrical from one point, perpendicular on this symmetrical from the other point and an angle by the third different solutions. The last has annotation: at the night of the January 1, 1940 after the New Year's Eve 1939".
External links
- Plemelj's students: http://hcoonce.math.mankato.msus.edu/html/id.phtml?id=20359
Sources
- Josip Plemelj, Iz mojega življenja in dela (From my life and work), Obzornik mat. fiz. 39 (1992) pp 188–192.
-
-

