
Kobayashi metric
Encyclopedia
In mathematics, the original Kobayashi metric is a pseudometric
(or pseudodistance) on complex manifold
s introduced by . It can be viewed as the dual of the Carathéodory metric
, and has been extended to complex analytic space
s and almost complex manifold
s. On Teichmüller space
the Kobayashi metric coincides with the Teichmüller metric; on the unit ball, it coincides with the Bergman metric
.
An analogous pseudodistance was constructed for flat affine and projective structures in and then generalized to (normal) projective connection
s. Essentially the same construction has been applied to (normal, pseudo-Riemannian) conformal connection
s and, more recently, to general (regular) parabolic geometries.
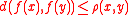 ,
,
for all holomorphic maps f from the unit disk D to X (where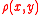 denotes distance in the Poincaré metric
denotes distance in the Poincaré metric
on D).
Pseudometric space
In mathematics, a pseudometric space is a generalized metric space in which the distance between two distinct points can be zero. In the same way as every normed space is a metric space, every seminormed space is a pseudometric space...
(or pseudodistance) on complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s introduced by . It can be viewed as the dual of the Carathéodory metric
Carathéodory metric
In mathematics, the Carathéodory metric is a metric defined on the open unit ball of a complex Banach space that has many similar properties to the Poincaré metric of hyperbolic geometry. It is named after the Greek mathematician Constantin Carathéodory....
, and has been extended to complex analytic space
Complex analytic space
In mathematics, a complex analytic space is a generalization of a complex manifold which allows the presence of singularities. Complex analytic spaces are locally ringed spaces which are locally isomorphic to local model spaces, where a local model space is an open subset of the vanishing locus of...
s and almost complex manifold
Almost complex manifold
In mathematics, an almost complex manifold is a smooth manifold equipped with smooth linear complex structure on each tangent space. The existence of this structure is a necessary, but not sufficient, condition for a manifold to be a complex manifold. That is, every complex manifold is an almost...
s. On Teichmüller space
Teichmüller space
In mathematics, the Teichmüller space TX of a topological surface X, is a space that parameterizes complex structures on X up to the action of homeomorphisms that are isotopic to the identity homeomorphism...
the Kobayashi metric coincides with the Teichmüller metric; on the unit ball, it coincides with the Bergman metric
Bergman metric
In differential geometry, the Bergman metric is a Hermitian metric that can be defined on certain types of complex manifold. It is so called because it is derived from the Bergman kernel, both of which are named for Stefan Bergman.-Definition:...
.
An analogous pseudodistance was constructed for flat affine and projective structures in and then generalized to (normal) projective connection
Projective connection
In differential geometry, a projective connection is a type of Cartan connection on a differentiable manifold.The structure of a projective connection is modeled on the geometry of projective space, rather than the affine space corresponding to an affine connection. Much like affine connections,...
s. Essentially the same construction has been applied to (normal, pseudo-Riemannian) conformal connection
Conformal connection
In conformal differential geometry, a conformal connection is a Cartan connection on an n-dimensional manifold M arising as a deformation of the Klein geometry given by the celestial n-sphere, viewed as the homogeneous space...
s and, more recently, to general (regular) parabolic geometries.
Definition
If X is a complex manifold, the Kobayashi pseudometric d may be characterized as the largest pseudometric on X such that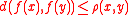 ,
,for all holomorphic maps f from the unit disk D to X (where
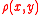 denotes distance in the Poincaré metric
denotes distance in the Poincaré metricPoincaré metric
In mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces.There are three equivalent...
on D).

