
Landau prime ideal theorem
Encyclopedia
In algebraic number theory
, the prime ideal theorem is the number field generalization of the prime number theorem
. It provides an asymptotic formula for counting the number of prime ideal
s of a number field K, with norm
at most X.
What to expect can be seen already for the Gaussian integer
s. There for any prime number p of the form 4n + 1, p factors as a product of two Gaussian primes of norm p. Primes of the form 4n + 3 remain prime, giving a Gaussian prime of norm p2. Therefore we should estimate

where r counts primes in the arithmetic progression 4n + 1, and r′ in the arithmetic progression 4n + 3. By the quantitative form of Dirichlet's theorem on primes, each of r(Y) and r′(Y) is asymptotically

Therefore the 2r(X) term predominates, and is asymptotically

This general pattern holds for number fields in general, so that the prime ideal theorem is dominated by the ideals of norm a prime number. As Edmund Landau
proved in , for norm at most X the same asymptotic formula
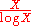
always holds. Heuristically this is because the logarithmic derivative
of the Dedekind zeta-function of K always has a simple pole with residue −1 at s = 1.
As with the Prime Number Theorem, a more precise estimate may be given in terms of the logarithmic integral function
. The number of prime ideals of norm ≤ X is
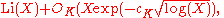
where cK is a constant depending on K.
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, the prime ideal theorem is the number field generalization of the prime number theorem
Prime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
. It provides an asymptotic formula for counting the number of prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s of a number field K, with norm
Field norm
In mathematics, the norm is a mapping defined in field theory, to map elements of a larger field into a smaller one.-Formal definitions:1. Let K be a field and L a finite extension of K...
at most X.
What to expect can be seen already for the Gaussian integer
Gaussian integer
In number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
s. There for any prime number p of the form 4n + 1, p factors as a product of two Gaussian primes of norm p. Primes of the form 4n + 3 remain prime, giving a Gaussian prime of norm p2. Therefore we should estimate

where r counts primes in the arithmetic progression 4n + 1, and r′ in the arithmetic progression 4n + 3. By the quantitative form of Dirichlet's theorem on primes, each of r(Y) and r′(Y) is asymptotically

Therefore the 2r(X) term predominates, and is asymptotically

This general pattern holds for number fields in general, so that the prime ideal theorem is dominated by the ideals of norm a prime number. As Edmund Landau
Edmund Landau
Edmund Georg Hermann Landau was a German Jewish mathematician who worked in the fields of number theory and complex analysis.-Biography:...
proved in , for norm at most X the same asymptotic formula
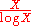
always holds. Heuristically this is because the logarithmic derivative
Logarithmic derivative
In mathematics, specifically in calculus and complex analysis, the logarithmic derivative of a function f is defined by the formulawhere f ′ is the derivative of f....
of the Dedekind zeta-function of K always has a simple pole with residue −1 at s = 1.
As with the Prime Number Theorem, a more precise estimate may be given in terms of the logarithmic integral function
Logarithmic integral function
In mathematics, the logarithmic integral function or integral logarithm li is a special function. It occurs in problems of physics and has number theoretic significance, occurring in the prime number theorem as an estimate of the number of prime numbers less than a given value.-Integral...
. The number of prime ideals of norm ≤ X is
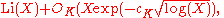
where cK is a constant depending on K.

