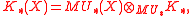Landweber exact functor theorem
Encyclopedia
In mathematics, the Landweber exact functor theorem, named after Peter Landweber, is an important theorem in algebraic topology
. It is known that a complex orientation of a homology theory
leads to a formal group law. The Landweber exact functor theorem (or LEFT for short) can be seen as a method to reverse this process: it constructs a homology theory out of a formal group law.
MU are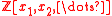
, where the degree of 
is 2i. This is isomorphic to the graded Lazard ring 
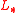. This means that giving a formal group law F (of degree −2) over a graded ring 
is equivalent to giving a graded ring morphism 
. Multiplication by an integer n >0 is defined inductively as a power series, by
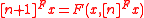and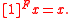 
Let now F be a formal group law over a ring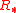
. Define for a topological space
X
Here
gets its 
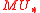-algebra structure via F. The question is: is E a homology theory? It is obviously a homotopy invariant functor, which fulfills excision. The problem is that tensoring in general does not preserve exact sequences. One could demand that 
is flat
over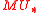
, but that would be too strong in practice. Peter Landweber found another criterion:
In particular, every formal group law F over a ring R yields a module over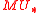
since we get via F a ring morphism 
.
K. Complex K-theory is complex oriented and has as formal group law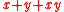
. The corresponding morphism 
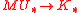is also known as the Todd genus. We have then an isomorphism
called the Conner–Floyd isomorphism.
While complex K-theory was constructed before by geometric means, many homology theories were first constructed via the Landweber exact functor theorem. This includes elliptic homology
, the Johnson–Wilson theories
and the Lubin–Tate spectra 
.
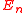While homology with rational coefficients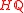
is Landweber exact, homology with integer coefficients 
is not Landweber exact. Furthermore, Morava K-theory
K(n) is not Landweber exact.
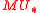is the same as a quasi-coherent sheaf
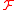over 
, where L is the Lazard ring. If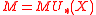 
, then M has the extra datum of a 
coaction. A coaction on the ring level corresponds to that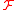 
is an equivariant sheaf with respect to an action of an affine group scheme G. It is a theorem of Quillen that 
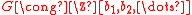and assigns to every ring R the group of power series
.
It acts on the set of formal group laws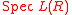
via
.
These are just the coordinate changes of formal group laws. Therefore, one can identify the stack
quotient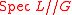
with the stack of (1-dimensional) formal group
s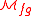
and 
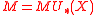defines a quasi-coherent sheaf over this stack. Now it is quite easy to see that it suffices that M defines a quasi-coherent sheaf 
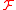which is flat over 
in order that 
is a homology theory. The Landweber exactness theorem can then be interpreted as a flatness criterion for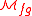 
(see Lurie 2010).
Refinements to
While the LEFT is known to produce (homotopy) ring spectra out of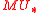 
, it is a much more delicate question to understand when these spectra are actually 
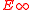-ring spectra
. As of 2010, the best progress was made by Jacob Lurie
. If X is an algebraic stack and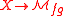
a flat map of stacks, the discussion above shows that we get a presheaf of (homotopy) ring spectra on X. If this map factors over 
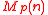(the stack of 1-dimensional p-divisible groups of height n) and the map 
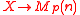is etale
, then this presheaf can be refined to a sheaf of
-ring spectra (see Goerss). This theorem is important for the construction of topological modular forms
.
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
. It is known that a complex orientation of a homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
leads to a formal group law. The Landweber exact functor theorem (or LEFT for short) can be seen as a method to reverse this process: it constructs a homology theory out of a formal group law.
Statement
The coefficients of complex cobordismComplex cobordism
In mathematics, complex cobordism is a generalized cohomology theory related to cobordism of manifolds. Its spectrum is denoted by MU. It is an exceptionally powerful cohomology theory, but can be quite hard to compute, so often instead of using it directly one uses some slightly weaker theories...
MU are
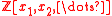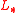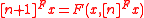, where the degree of is 2i. This is isomorphic to the graded Lazard ring . This means that giving a formal group law F (of degree −2) over a graded ring is equivalent to giving a graded ring morphism . Multiplication by an integer n >0 is defined inductively as a power series, by and 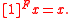Let now F be a formal group law over a ring
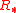. Define for a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X
Here
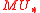gets its -algebra structure via F. The question is: is E a homology theory? It is obviously a homotopy invariant functor, which fulfills excision. The problem is that tensoring in general does not preserve exact sequences. One could demand that is flatFlat module
In Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
over
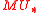, but that would be too strong in practice. Peter Landweber found another criterion:- Theorem (Landweber exact functor theorem)
- Let p be a prime and
be the coefficient of 
in 
, where U is the universal formal group law over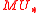 
. Now suppose that 
is a graded 
-module and the sequence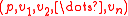 
is regularRegular sequence (algebra)In commutative algebra, if R is a commutative ring and M an R-module, a nonzero element r in R is called M-regular if r is not a zerodivisor on M, and M/rM is nonzero...
for M, for every p and n. Then - is a homology theory on CW-complexes.
In particular, every formal group law F over a ring R yields a module over
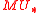since we get via F a ring morphism .Remarks
- There is also a version for Brown–Peterson cohomologyBrown–Peterson cohomologyIn mathematics, Brown–Peterson cohomology is a generalized cohomology theory introduced by, depending on a choice of prime p. It is described in detail by .Its representing spectrum is denoted by BP.-Complex cobordism and Quillen's idempotent:...
BP. The spectrumSpectrum (homotopy theory)In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory....
BP is a direct summand of
with coefficients 
. The statement of the LEFT stays true if one fixes a prime p and substitutes BP for MU.
- The classical proof of the LEFT uses the Landweber–Morava invariant ideal theorem: the only prime ideals of
which are invariant under coaction of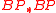 
are the 
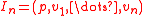. This allows to check flatness only against the 
(see Landweber, 1976).
- The LEFT can be strengthened as follows: let
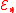be the (homotopy) category of Landweber exact 
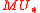-modules and 
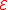the category of MU-module spectra M such that 
is Landweber exact. Then the functor 
is an equivalence of categories. The inverse functor (given by the LEFT) takes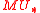 
-algebras to (homotopy) MU-algebra spectra (see Hovey, Strickland, 1999, Thm 2.7).
Examples
The archetypical and first known (non-trivial) example is complex K-theoryTopological K-theory
In mathematics, topological K-theory is a branch of algebraic topology. It was founded to study vector bundles on general topological spaces, by means of ideas now recognised as K-theory that were introduced by Alexander Grothendieck...
K. Complex K-theory is complex oriented and has as formal group law
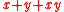. The corresponding morphism 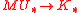is also known as the Todd genus. We have then an isomorphism
called the Conner–Floyd isomorphism.
While complex K-theory was constructed before by geometric means, many homology theories were first constructed via the Landweber exact functor theorem. This includes elliptic homology
Elliptic cohomology
In mathematics, elliptic cohomology is a cohomology theory in the sense of algebraic topology. It is related to elliptic curves and modular forms.-History and motivation:Historically, elliptic cohomology arose from the study of elliptic genera...
, the Johnson–Wilson theories
Johnson–Wilson theory
In algebraic topology, Johnson–Wilson theory E is a generalized cohomology theory introduced by . Real Johnson–Wilson theory ER was introduced by ....
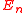and the Lubin–Tate spectra .While homology with rational coefficients
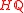is Landweber exact, homology with integer coefficients is not Landweber exact. Furthermore, Morava K-theoryMorava K-theory
In stable homotopy theory, a branch of mathematics, Morava K-theory is one of a collection of cohomology theories introduced in algebraic topology by Jack Morava in unpublished preprints in the early 1970s...
K(n) is not Landweber exact.
Modern reformulation
A module M over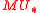 is the same as a quasi-coherent sheafCoherent sheaf
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...
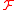over , where L is the Lazard ring. If 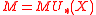, then M has the extra datum of a coaction. A coaction on the ring level corresponds to that is an equivariant sheaf with respect to an action of an affine group scheme G. It is a theorem of Quillen that 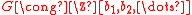and assigns to every ring R the group of power series.It acts on the set of formal group laws
via.These are just the coordinate changes of formal group laws. Therefore, one can identify the stack
Stack (descent theory)
In mathematics a stack is a concept used to formalise some of the main constructions of descent theory.Descent theory is concerned with generalisations of situations where geometrical objects can be "glued together" when they are isomorphic when restricted to intersections of the sets in an open...
quotient
with the stack of (1-dimensional) formal groupFormal group
In mathematics, a formal group law is a formal power series behaving as if it were the product of a Lie group. They were introduced by . The term formal group sometimes means the same as formal group law, and sometimes means one of several generalizations. Formal groups are intermediate between...
s
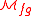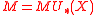and defines a quasi-coherent sheaf over this stack. Now it is quite easy to see that it suffices that M defines a quasi-coherent sheaf 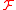which is flat over in order that is a homology theory. The Landweber exactness theorem can then be interpreted as a flatness criterion for 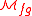(see Lurie 2010).Refinements to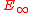 
-ring spectra
While the LEFT is known to produce (homotopy) ring spectra out of 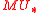, it is a much more delicate question to understand when these spectra are actually 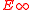-ring spectraHighly structured ring spectrum
In mathematics, a highly structured ring spectrum or A_\infty-ring is an object in homotopy theory encoding a refinement of a multiplicative structure on a cohomology theory. A commutative version of an A_\infty-ring is called an E_\infty-ring...
. As of 2010, the best progress was made by Jacob Lurie
Jacob Lurie
Jacob Alexander Lurie is an American mathematician, who is currently a professor at Harvard University.-Life:While in school, Lurie took part in the International Mathematical Olympiad, where he won a gold medal with a perfect score in 1994...
. If X is an algebraic stack and
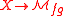a flat map of stacks, the discussion above shows that we get a presheaf of (homotopy) ring spectra on X. If this map factors over 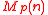(the stack of 1-dimensional p-divisible groups of height n) and the map 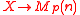is etaleÉtale
In mathematics, more specifically in algebra, the adjective étale refers to several closely related concepts:* Étale morphism** Formally étale morphism* Étale cohomology* Étale topology* Étale fundamental group* Étale space* Étale group scheme...
, then this presheaf can be refined to a sheaf of
-ring spectra (see Goerss). This theorem is important for the construction of topological modular formsTopological modular forms
In mathematics, the spectrum of topological modular forms describes a generalized cohomology theory whose coefficient ring is related to the graded ring of holomorphic modular forms with integral cusp expansions...
.