
Lichnerowicz formula
Encyclopedia
The Lichnerowicz formula (also known as the Lichnerowicz–Weitzenböck formula) is a fundamental equation in the analysis of spinor
s on pseudo-Riemannian manifold
s. In dimension 4, it forms a piece of Seiberg–Witten theory and other aspects of gauge theory
. It is named after noted mathematician André Lichnerowicz
who proved it in 1963. The formula gives a relationship between the Dirac operator
and the Laplace-Beltrami operator
acting on spinors, in which the scalar curvature
appears in a natural way. The result is significant because it provides an interface between results from the study of elliptic partial differential equations, results concerning the scalar curvature, and results on spinors and spin structures.
Given a spin structure
on a pseudo-Riemannian manifold M and a spinor bundle S, the Lichnerowicz formula states that on a section ψ of S,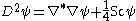
where Sc denotes the scalar curvature
and is the connection Laplacian. More generally, given a complex spin structure on a pseudo-Riemannian manifold M, a spinor bundle W± with section
is the connection Laplacian. More generally, given a complex spin structure on a pseudo-Riemannian manifold M, a spinor bundle W± with section 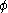 , and a connection A on its determinant line bundle L, the Lichnerowicz formula is
, and a connection A on its determinant line bundle L, the Lichnerowicz formula is
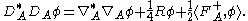
Here,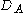 is the Dirac operator
is the Dirac operator
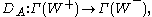 and
and 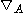 is the covariant derivative associated with the connection A,
is the covariant derivative associated with the connection A,  .
. 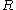 is the usual scalar curvature (a contraction of the Ricci tensor
is the usual scalar curvature (a contraction of the Ricci tensor
) and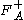 is the self-dual part of the curvature of A. The asterisks denote the adjoint of the quantity and the brackets
is the self-dual part of the curvature of A. The asterisks denote the adjoint of the quantity and the brackets 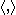 denote the Clifford action
denote the Clifford action
.
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s on pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
s. In dimension 4, it forms a piece of Seiberg–Witten theory and other aspects of gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
. It is named after noted mathematician André Lichnerowicz
André Lichnerowicz
André Lichnerowicz was a noted French differential geometer and mathematical physicist of Polish descent.-Biography:...
who proved it in 1963. The formula gives a relationship between the Dirac operator
Dirac operator
In mathematics and quantum mechanics, a Dirac operator is a differential operator that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian...
and the Laplace-Beltrami operator
Laplace-Beltrami operator
In differential geometry, the Laplace operator, named after Pierre-Simon Laplace, can be generalized to operate on functions defined on surfaces in Euclidean space and, more generally, on Riemannian and pseudo-Riemannian manifolds. This more general operator goes by the name Laplace–Beltrami...
acting on spinors, in which the scalar curvature
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
appears in a natural way. The result is significant because it provides an interface between results from the study of elliptic partial differential equations, results concerning the scalar curvature, and results on spinors and spin structures.
Given a spin structure
Spin structure
In differential geometry, a spin structure on an orientable Riemannian manifold \,allows one to define associated spinor bundles, giving rise to the notion of a spinor in differential geometry....
on a pseudo-Riemannian manifold M and a spinor bundle S, the Lichnerowicz formula states that on a section ψ of S,
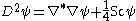
where Sc denotes the scalar curvature
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
and
 is the connection Laplacian. More generally, given a complex spin structure on a pseudo-Riemannian manifold M, a spinor bundle W± with section
is the connection Laplacian. More generally, given a complex spin structure on a pseudo-Riemannian manifold M, a spinor bundle W± with section 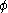 , and a connection A on its determinant line bundle L, the Lichnerowicz formula is
, and a connection A on its determinant line bundle L, the Lichnerowicz formula is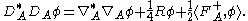
Here,
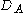 is the Dirac operator
is the Dirac operatorDirac operator
In mathematics and quantum mechanics, a Dirac operator is a differential operator that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian...
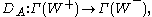 and
and 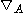 is the covariant derivative associated with the connection A,
is the covariant derivative associated with the connection A,  .
. 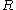 is the usual scalar curvature (a contraction of the Ricci tensor
is the usual scalar curvature (a contraction of the Ricci tensorRicci curvature
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space...
) and
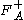 is the self-dual part of the curvature of A. The asterisks denote the adjoint of the quantity and the brackets
is the self-dual part of the curvature of A. The asterisks denote the adjoint of the quantity and the brackets 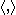 denote the Clifford action
denote the Clifford actionClifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
.

