
Spinor bundle
Encyclopedia
In differential geometry, given a spin structure
on a -dimensional Riemannian manifold
-dimensional Riemannian manifold
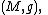 one defines the spinor bundle to be the complex vector bundle
one defines the spinor bundle to be the complex vector bundle 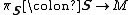 associated to the corresponding principal bundle
associated to the corresponding principal bundle
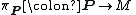 of spin frames over
of spin frames over 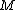 and the spin representation of its structure group
and the spin representation of its structure group 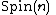 on the space of spinor
on the space of spinor
s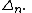 .
.
A section of the spinor bundle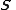 is called a spinor field.
is called a spinor field.
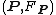 be a spin structure
be a spin structure
on a Riemannian manifold
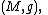 that is, an equivariant
that is, an equivariant
lift of the oriented orthonormal frame bundle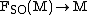 with respect to the double covering
with respect to the double covering 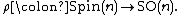
The spinor bundle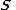 is defined to be the complex vector bundle
is defined to be the complex vector bundle
associated to the spin structure
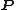 via the spin representation
via the spin representation 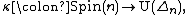 where
where 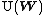 denotes the group
denotes the group
of unitary operator
s acting on a Hilbert space
 It is worth noting that the spin representation
It is worth noting that the spin representation  is a faithful and unitary representation
is a faithful and unitary representation
of the group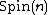 .
.
Spin structure
In differential geometry, a spin structure on an orientable Riemannian manifold \,allows one to define associated spinor bundles, giving rise to the notion of a spinor in differential geometry....
on a
 -dimensional Riemannian manifold
-dimensional Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
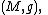 one defines the spinor bundle to be the complex vector bundle
one defines the spinor bundle to be the complex vector bundle 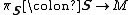 associated to the corresponding principal bundle
associated to the corresponding principal bundlePrincipal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
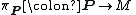 of spin frames over
of spin frames over 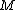 and the spin representation of its structure group
and the spin representation of its structure group 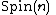 on the space of spinor
on the space of spinorSpinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s
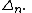 .
.A section of the spinor bundle
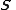 is called a spinor field.
is called a spinor field.Formal definition
Let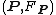 be a spin structure
be a spin structureSpin structure
In differential geometry, a spin structure on an orientable Riemannian manifold \,allows one to define associated spinor bundles, giving rise to the notion of a spinor in differential geometry....
on a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
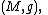 that is, an equivariant
that is, an equivariantEquivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
lift of the oriented orthonormal frame bundle
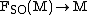 with respect to the double covering
with respect to the double covering 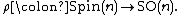
The spinor bundle
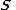 is defined to be the complex vector bundle
is defined to be the complex vector bundle
associated to the spin structure
Spin structure
In differential geometry, a spin structure on an orientable Riemannian manifold \,allows one to define associated spinor bundles, giving rise to the notion of a spinor in differential geometry....
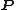 via the spin representation
via the spin representation 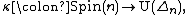 where
where 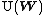 denotes the group
denotes the groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
s acting on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
 It is worth noting that the spin representation
It is worth noting that the spin representation  is a faithful and unitary representation
is a faithful and unitary representationUnitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
of the group
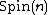 .
.See also
- Orthonormal frame bundle
- SpinorSpinorIn mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
- Spin manifold
- Spinor representationSpinor representationIn mathematics, the spin representations are particular projective representations of the orthogonal or special orthogonal groups in arbitrary dimension and signature . More precisely, they are representations of the spin groups, which are double covers of the special orthogonal groups...


