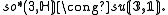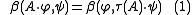Spinor representation
Encyclopedia
In mathematics
, the spin representations are particular projective representation
s of the orthogonal
or special orthogonal groups in arbitrary dimension
and signature
(i.e., including indefinite orthogonal groups). More precisely, they are representations
of the spin groups, which are double covers of the special orthogonal groups. They are usually studied over the real
or complex number
s, but they can be defined over other field
s.
Elements of a spin representation are called spinor
s. They play an important role in the physical
description of fermion
s such as the electron
.
The spin representations may be constructed in several ways, but typically the construction involves (perhaps only implicitly) the choice of a maximal isotropic subspace in the vector representation of the group. Over the real numbers, this usually requires using a complexification of the vector representation. For this reason, it is convenient to define the spin representations over the complex numbers first, and derive real representation
s by introducing real structure
s.
The properties of the spin representations depend, in a subtle way, on the dimension and signature of the orthogonal group. In particular, spin representations often admit invariant
bilinear forms, which can be used to embed
the spin groups into classical Lie groups. In low dimensions, these embeddings are surjective and determine special isomorphisms between the spin groups and more familiar Lie groups; this elucidates the properties of spinors in these dimensions.
real or complex vector space
with a nondegenerate quadratic form
Q. The (real or complex) linear maps preserving Q form the orthogonal group
O(V,Q). The identity component of the group is called the special orthogonal group SO(V,Q). (For V real with an indefinite quadratic form, this terminology is not standard: the special orthogonal group is usually defined to be a subgroup with two components in this case.) Up to group isomorphism
, SO(V,Q) has a unique connected
double cover, the spin group Spin(V,Q). There is thus a group homomorphism
Spin(V,Q) → SO(V,Q) whose kernel has two elements denoted {1, −1}, where 1 is the identity element
.
O(V,Q), SO(V,Q) and Spin(V,Q) are all Lie groups, and for fixed (V,Q) they have the same Lie algebra
, so(V,Q). If V is real, then V is a real vector subspace of its complexification
VC := V ⊗R C, and the quadratic form Q extends naturally to a quadratic form QC on VC. This embeds SO(V,Q) as a subgroup
of SO(VC, QC), and hence we may realise Spin(V,Q) as a subgroup of Spin(VC, QC). Furthermore, so(VC, QC) is the complexification of so(V,Q).
In the complex case, quadratic forms are determined up to isomorphism by the dimension n of V. Concretely, we may assume V=Cn and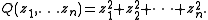
The corresponding Lie groups and Lie algebra are denoted O(n,C), SO(n,C), Spin(n,C) and so(n,C).
In the real case, quadratic forms are determined up to isomorphism by a pair of nonnegative integers (p,q) where n:=p+q is the dimension of V, and p-q is the signature
. Concretely, we may assume V=Rn and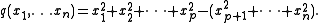
The corresponding Lie groups and Lie algebra are denoted O(p,q), SO(p,q), Spin(p,q) and so(p,q). We write Rp,q in place of Rn to make the signature explicit.
The spin representations are, in a sense, the simplest representation
s of Spin(n,C) and Spin(p,q) that do not come from representations of SO(n,C) and SO(p,q). A spin representation is, therefore, a real or complex vector space S together with a group homomorphism ρ from Spin(n,C) or Spin(p,q) to the general linear group
GL(S) such that the element −1 is not in the kernel of ρ.
If S is such a representation, then according to the relation between Lie groups and Lie algebras, it induces a Lie algebra representation, i.e., a Lie algebra homomorphism from so(n,C) or so(p,q) to the Lie algebra gl(S) of endomorphisms of S with the commutator bracket.
Spin representations can be analysed according to the following strategy: if S is a real spin representation of Spin(p,q), then its complexification is a complex spin representation of Spin(p,q); as a representation of so(p,q), it therefore extends to a complex representation of so(n,C). Proceeding in reverse, we therefore first construct complex spin representations of Spin(n,C) and so(n,C), then restrict them to complex spin representations of so(p,q) and Spin(p,q), then finally analyse possible reductions to real spin representations.
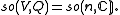
The symmetric bilinear form
on V associated to Q by polarization is denoted <.,.>.
of maximal isotropic subspaces of V with W ∩ W∗ = 0. Let us make such a choice. If n = 2m or n = 2m+1, then W and W∗ both have dimension m. If n = 2m, then V = W ⊕ W∗, whereas if n = 2m+1, then V = W ⊕ U ⊕ W∗, where U is the 1-dimensional orthogonal complement to W ⊕ W∗. The bilinear form <.,.> induces a pairing between W and W∗, which must be nondegenerate, because W and W∗ are isotropic subspaces and Q is nondegenerate. Hence W and W∗ are dual vector spaces.
More concretely, let a1, ... am be a basis for W. Then there is a unique basis α1, ... αm of W∗ such that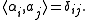
If A is a m × m matrix, then A induces a endomorphism of W with respect to this basis and the transpose AT induces a transformation of W∗ with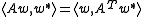
for all w in W and w* in W∗. It follows that the endomorphism ρA of V, equal to A on W, − AT on W∗ and zero on U (if n is odd), is skew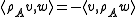
and hence an element of so(n,C).
Using the diagonal matrices in this construction defines a Cartan subalgebra h of so(n,C): the rank of so(n,C) is m, and the diagonal m × m matrices determine an m-dimensional abelian subalgebra.
Let ε1, ... εm be the basis of h∗ such that, for a diagonal matrix A, εk(ρA) is the kth diagonal entry of A. Clearly this is a basis for h∗. Since the bilinear form identifies so(n,C) with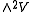
, it is now easy to construct the root system
associated to h. The root spaces (simultaneous eigenspaces for the action of h) are spanned by the following elements: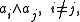
with root
(simultaneous eigenvalue)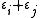
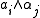(which is in h if i = j) with root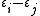 
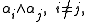with root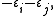 
and, if n is odd, and u is a nonzero element of U,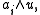
with root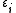 
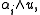with root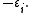 
Thus, with respect the basis ε1, ... εm, the roots are the vectors in h∗ that are permutations of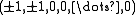
together with the permutations of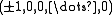
if n = 2m+1 is odd.
A system of positive roots is given by εi+εj (i≠j), εi−εj (i<j) and (for n odd) εi. The corresponding simple root
s are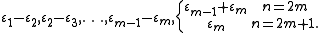
The positive roots are nonnegative integer linear combinations of the simple roots.
(s)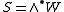
and/or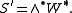 
There is an action of V on S such that for any element v = w+w* in W ⊕ W∗ and any ψ in S the action is given by: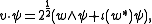
where the second term is a contraction (interior multiplication) defined using the bilinear form, which pairs W and W∗. This action respects the Clifford relations v2 = Q(v)1, and so induces a homomorphism from the Clifford algebra
ClnC of V to End(S). A similar action can be defined on S′, so that both S and S′ are Clifford modules.
The Lie algebra so(n,C) is isomorphic to the complexified Lie algebra spinnC in ClnC via the mapping induced by the covering Spin(n) → SO(n)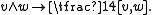
It follows that both S and S′ are representations of so(n,C). They are actually equivalent
representations, so we focus on S.
The explicit description shows that the elements αi∧ai of the Cartan subalgebra h act on S by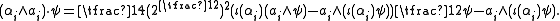
A basis for S is given by elements of the form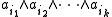
for 0 ≤ k ≤ m and i1 < ... < ik. These clearly span weight spaces for the action of h: αi∧ai has eigenvalue -1/2 on the given basis vector if i = ij for some j, and has eigenvalue 1/2 otherwise.
It follows that the weights
of S are all possible combinations of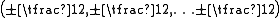
and each weight space is one dimensional. Elements of S are called Dirac spinors.
When n is even, S is not an irreducible representation: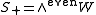
and 
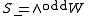are invariant subspaces. The weights divide into those with an even number of minus signs, and those with an odd number of minus signs. Both S+ and S− are irreducible representations of dimension 2m−1 whose elements are called Weyl spinors. They are also known as chiral spin representations or half-spin representations. With respect to the positive root system above, the highest weights of S+ and S− are
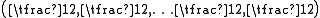and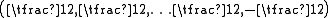 
respectively. The Clifford action identifies ClnC with End(S) and the even subalgebra is identified with the endomorphisms preserving S+ and S−. The other Clifford module S′ is isomorphic
to S in this case.
When n is odd, S is an irreducible representation of so(n,C) of dimension 2m: the Clifford action of a unit vector u ∈ U is given by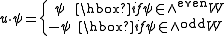
and so elements of so(n,C) of the form u∧w or u∧w* do not preserve the even and odd parts of the exterior algebra of W. The highest weight of S is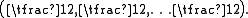
The Clifford action is not faithful on S: ClnC can be identified with End(S) ⊕ End(S′), where u acts with the opposite sign on S′. More precisely, the two representations are related by the parity involution α of ClnC (also known as the principal automorphism), which is the identity on the even subalgebra, and minus the identity on the odd part of ClnC. In other words, there is a linear isomorphism from S to S′, which identifies the action of A in ClnC on S with the action of α(A) on S′.
S∗.
When n = 2m+1 is odd, the isomorphism B: S → S∗ is unique up to scale by Schur's lemma
, since S is irreducible, and it defines a nondegenerate invariant bilinear form β on S via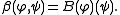
Here invariance means that
for all ξ in so(n,C) and φ, ψ in S — in other words the action of ξ is skew with respect to β. In fact, more is true: S∗ is a representation of the opposite
Clifford algebra, and therefore, since ClnC only has two nontrivial simple module
s S and S′, related by the parity involution α, there is an antiautomorphism τ of ClnC such that
for any A in ClnC. In fact τ is reversion (the antiautomorphism induced by the identity on V) for m even, and conjugation (the antiautomorphism induced by minus the identity on V) for m odd. These two antiautomorphisms are related by parity involution α, which is the automorphism induced by minus the identity on V. Both satisfy τ(ξ) = −ξ for ξ in so(n,C).
When n = 2m, the situation depends more sensitively upon the parity of m. For m even, a weight λ has an even number of minus signs if and only if −λ does; it follows that there are separate isomorphisms B±: S± → S±∗ of each half-spin representation with its dual, each determined uniquely up to scale. These may be combined into an isomorphism B: S → S∗. For m odd, λ is a weight of S+ if and only if −λ is a weight of S−; thus there is an isomorphism from S+ to S−∗, again unique up to scale, and its transpose provides an isomorphism from S− to S+∗. These may again be combined into an isomorphism B: S → S∗.
For both m even and m odd, the freedom in the choice of B may be restricted to an overall scale by insisting that the bilinear form β corresponding to B satisfies (1), where τ is a fixed antiautomorphism (either reversion or conjugation).
linear maps S ⊗ S → ∧kV∗ correspond bijectively to invariant maps ∧kV ⊗ S ⊗ S → C and nonzero such maps can be constructed via the inclusion of ∧kV into the Clifford algebra. Furthermore if β(φ,ψ) = ε β(ψ,φ) and τ has sign εk on ∧kV then
for A in ∧kV.
If n = 2m+1 is odd then it follows from Schur's Lemma that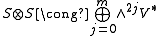
(both sides have dimension 22m and the representations on the right are inequivalent). Because the symmetries are governed by an involution τ that is either conjugation or reversion, the symmetry of the ∧2jV∗ component alternates with j. Elementary combinatorics gives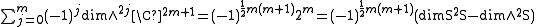
and the sign determines which representations occur in S2S and which occur in ∧2S. In particular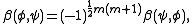
and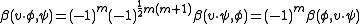
for v ∈ V (which is isomorphic to ∧2mV), confirming that τ is reversion for m even, and conjugation for m odd.
If n=2m is even, then the analysis is more involved, but the result is a more refined decomposition: S2S±, ∧2S± and S+ ⊗ S− can each be decomposed as a direct sum of k-forms (where for k=m there is a further decomposition into selfdual and antiselfdual m-forms).
The main outcome is a realisation of so(n,C) as a subalgebra of a classical Lie algebra on S, depending upon n modulo 8, according to the following table:
For n ≤ 6, these embeddings are isomorphisms (onto sl rather than gl for n=6):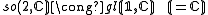
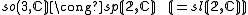
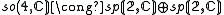
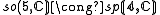
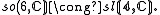
The type of structure invariant under so(p,q) depends only on the signature p−q modulo 8, and is given by the following table.
Here R, C and H denote real, hermitian and quaternionic structures respectively, and R+R and H+H indicate that the half-spin representations both admit real or quaternionic structures respectively.
The odd case is simpler, there is only one complex spin representation S, and hermitian structures do not occur. Apart from the trivial case n = 1, S is always even dimensional, say dim S = 2N. The real forms of so(2N,C) are so(K,L) with K + L = 2N and so*(N,H), while the real forms of sp(2N,C) are sp(2N,R) and sp(K,L) with K + L = N. The presence of a Clifford action of V on S forces K = L in both cases unless pq = 0, in which case KL=0, which is denoted simply so(2N) or sp(N). Hence the odd spin representations may be summarized in the following table.
(†) N is even for n>3 and for n=3, this is sp(1).
The even dimensional case is similar. For n>2, the complex half-spin representations are even dimensional. We have additionally to deal with hermitian structures and the real forms of sl(2N,C), which are sl(2N,R), su(K,L) with K + L = 2N, and sl(N,H). The resulting even spin representations are summarized as follows.
(*) For pq=0, we have instead so(2N)+so(2N)
(†) N is even for n>4 and for pq=0 (which includes n=4 with N=1), we have instead sp(N)+sp(N)
The low dimensional isomorphisms in the complex case have the following real forms.
The only special isomorphism of real Lie algebras missing from this table is
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the spin representations are particular projective representation
Projective representation
In the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
s of the orthogonal
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
or special orthogonal groups in arbitrary dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
and signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
(i.e., including indefinite orthogonal groups). More precisely, they are representations
Representation of a Lie group
In mathematics and theoretical physics, the idea of a representation of a Lie group plays an important role in the study of continuous symmetry. A great deal is known about such representations, a basic tool in their study being the use of the corresponding 'infinitesimal' representations of Lie...
of the spin groups, which are double covers of the special orthogonal groups. They are usually studied over the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, but they can be defined over other field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s.
Elements of a spin representation are called spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s. They play an important role in the physical
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
description of fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s such as the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
.
The spin representations may be constructed in several ways, but typically the construction involves (perhaps only implicitly) the choice of a maximal isotropic subspace in the vector representation of the group. Over the real numbers, this usually requires using a complexification of the vector representation. For this reason, it is convenient to define the spin representations over the complex numbers first, and derive real representation
Real representation
In the mathematical field of representation theory a real representation is usually a representation on a real vector space U, but it can also mean a representation on a complex vector space V with an invariant real structure, i.e., an antilinear equivariant mapj\colon V\to V\,which...
s by introducing real structure
Real structure
In mathematics, a real structure on a complex vector space is a way to decompose the complex vector space in the direct sum of two real vector spaces...
s.
The properties of the spin representations depend, in a subtle way, on the dimension and signature of the orthogonal group. In particular, spin representations often admit invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
bilinear forms, which can be used to embed
Injection (medicine)
An injection is an infusion method of putting fluid into the body, usually with a hollow needle and a syringe which is pierced through the skin to a sufficient depth for the material to be forced into the body...
the spin groups into classical Lie groups. In low dimensions, these embeddings are surjective and determine special isomorphisms between the spin groups and more familiar Lie groups; this elucidates the properties of spinors in these dimensions.
Set up
Let V be a finite dimensionalDimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
real or complex vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
with a nondegenerate quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
Q. The (real or complex) linear maps preserving Q form the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(V,Q). The identity component of the group is called the special orthogonal group SO(V,Q). (For V real with an indefinite quadratic form, this terminology is not standard: the special orthogonal group is usually defined to be a subgroup with two components in this case.) Up to group isomorphism
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
, SO(V,Q) has a unique connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
double cover, the spin group Spin(V,Q). There is thus a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
Spin(V,Q) → SO(V,Q) whose kernel has two elements denoted {1, −1}, where 1 is the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
.
O(V,Q), SO(V,Q) and Spin(V,Q) are all Lie groups, and for fixed (V,Q) they have the same Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, so(V,Q). If V is real, then V is a real vector subspace of its complexification
Complexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
VC := V ⊗R C, and the quadratic form Q extends naturally to a quadratic form QC on VC. This embeds SO(V,Q) as a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of SO(VC, QC), and hence we may realise Spin(V,Q) as a subgroup of Spin(VC, QC). Furthermore, so(VC, QC) is the complexification of so(V,Q).
In the complex case, quadratic forms are determined up to isomorphism by the dimension n of V. Concretely, we may assume V=Cn and
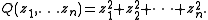
The corresponding Lie groups and Lie algebra are denoted O(n,C), SO(n,C), Spin(n,C) and so(n,C).
In the real case, quadratic forms are determined up to isomorphism by a pair of nonnegative integers (p,q) where n:=p+q is the dimension of V, and p-q is the signature
Sylvester's law of inertia
Sylvester's law of inertia is a theorem in matrix algebra about certain properties of the coefficient matrix of a real quadratic form that remain invariant under a change of coordinates...
. Concretely, we may assume V=Rn and
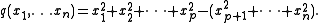
The corresponding Lie groups and Lie algebra are denoted O(p,q), SO(p,q), Spin(p,q) and so(p,q). We write Rp,q in place of Rn to make the signature explicit.
The spin representations are, in a sense, the simplest representation
Representation of a Lie group
In mathematics and theoretical physics, the idea of a representation of a Lie group plays an important role in the study of continuous symmetry. A great deal is known about such representations, a basic tool in their study being the use of the corresponding 'infinitesimal' representations of Lie...
s of Spin(n,C) and Spin(p,q) that do not come from representations of SO(n,C) and SO(p,q). A spin representation is, therefore, a real or complex vector space S together with a group homomorphism ρ from Spin(n,C) or Spin(p,q) to the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(S) such that the element −1 is not in the kernel of ρ.
If S is such a representation, then according to the relation between Lie groups and Lie algebras, it induces a Lie algebra representation, i.e., a Lie algebra homomorphism from so(n,C) or so(p,q) to the Lie algebra gl(S) of endomorphisms of S with the commutator bracket.
Spin representations can be analysed according to the following strategy: if S is a real spin representation of Spin(p,q), then its complexification is a complex spin representation of Spin(p,q); as a representation of so(p,q), it therefore extends to a complex representation of so(n,C). Proceeding in reverse, we therefore first construct complex spin representations of Spin(n,C) and so(n,C), then restrict them to complex spin representations of so(p,q) and Spin(p,q), then finally analyse possible reductions to real spin representations.
Complex spin representations
Let V=Cn with the standard quadratic form Q so that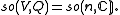The symmetric bilinear form
Symmetric bilinear form
A symmetric bilinear form is a bilinear form on a vector space that is symmetric. Symmetric bilinear forms are of great importance in the study of orthogonal polarity and quadrics....
on V associated to Q by polarization is denoted <.,.>.
Isotropic subspaces and root systems
A standard construction of the spin representations of so(n,C) begins with a choice of a pair (W, W∗)of maximal isotropic subspaces of V with W ∩ W∗ = 0. Let us make such a choice. If n = 2m or n = 2m+1, then W and W∗ both have dimension m. If n = 2m, then V = W ⊕ W∗, whereas if n = 2m+1, then V = W ⊕ U ⊕ W∗, where U is the 1-dimensional orthogonal complement to W ⊕ W∗. The bilinear form <.,.> induces a pairing between W and W∗, which must be nondegenerate, because W and W∗ are isotropic subspaces and Q is nondegenerate. Hence W and W∗ are dual vector spaces.
More concretely, let a1, ... am be a basis for W. Then there is a unique basis α1, ... αm of W∗ such that
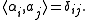
If A is a m × m matrix, then A induces a endomorphism of W with respect to this basis and the transpose AT induces a transformation of W∗ with
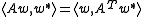
for all w in W and w* in W∗. It follows that the endomorphism ρA of V, equal to A on W, − AT on W∗ and zero on U (if n is odd), is skew
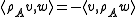
and hence an element of so(n,C).
Using the diagonal matrices in this construction defines a Cartan subalgebra h of so(n,C): the rank of so(n,C) is m, and the diagonal m × m matrices determine an m-dimensional abelian subalgebra.
Let ε1, ... εm be the basis of h∗ such that, for a diagonal matrix A, εk(ρA) is the kth diagonal entry of A. Clearly this is a basis for h∗. Since the bilinear form identifies so(n,C) with
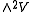, it is now easy to construct the root systemRoot system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
associated to h. The root spaces (simultaneous eigenspaces for the action of h) are spanned by the following elements:
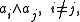with rootRoot system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
(simultaneous eigenvalue)
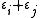
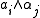(which is in h if i = j) with root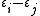 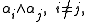with root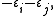 and, if n is odd, and u is a nonzero element of U,
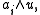with root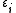 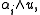with root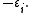 Thus, with respect the basis ε1, ... εm, the roots are the vectors in h∗ that are permutations of
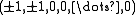
together with the permutations of
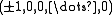
if n = 2m+1 is odd.
A system of positive roots is given by εi+εj (i≠j), εi−εj (i<j) and (for n odd) εi. The corresponding simple root
Simple root
in mathematics the term simple root can refer to one of two unrelated notions:*A simple root of a polynomial is a root of multiplicity one*A simple root in a root system is a member of a subset determined by a choice of positive roots...
s are
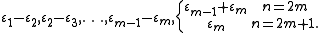
The positive roots are nonnegative integer linear combinations of the simple roots.
Spin representations and their weights
One construction of the spin representations of so(n,C) uses the exterior algebraExterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
(s)
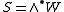and/or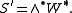 There is an action of V on S such that for any element v = w+w* in W ⊕ W∗ and any ψ in S the action is given by:
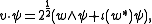
where the second term is a contraction (interior multiplication) defined using the bilinear form, which pairs W and W∗. This action respects the Clifford relations v2 = Q(v)1, and so induces a homomorphism from the Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
ClnC of V to End(S). A similar action can be defined on S′, so that both S and S′ are Clifford modules.
The Lie algebra so(n,C) is isomorphic to the complexified Lie algebra spinnC in ClnC via the mapping induced by the covering Spin(n) → SO(n)
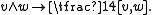
It follows that both S and S′ are representations of so(n,C). They are actually equivalent
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
representations, so we focus on S.
The explicit description shows that the elements αi∧ai of the Cartan subalgebra h act on S by
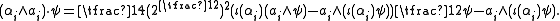
A basis for S is given by elements of the form
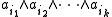
for 0 ≤ k ≤ m and i1 < ... < ik. These clearly span weight spaces for the action of h: αi∧ai has eigenvalue -1/2 on the given basis vector if i = ij for some j, and has eigenvalue 1/2 otherwise.
It follows that the weights
Weight (representation theory)
In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F – a linear functional – or equivalently, a one dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group...
of S are all possible combinations of
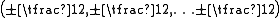
and each weight space is one dimensional. Elements of S are called Dirac spinors.
When n is even, S is not an irreducible representation:
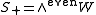and 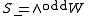are invariant subspaces. The weights divide into those with an even number of minus signs, and those with an odd number of minus signs. Both S+ and S− are irreducible representations of dimension 2m−1 whose elements are called Weyl spinors. They are also known as chiral spin representations or half-spin representations. With respect to the positive root system above, the highest weights of S+ and S− are 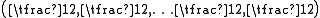and 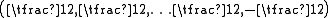respectively. The Clifford action identifies ClnC with End(S) and the even subalgebra is identified with the endomorphisms preserving S+ and S−. The other Clifford module S′ is isomorphic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to S in this case.
When n is odd, S is an irreducible representation of so(n,C) of dimension 2m: the Clifford action of a unit vector u ∈ U is given by
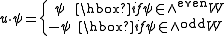
and so elements of so(n,C) of the form u∧w or u∧w* do not preserve the even and odd parts of the exterior algebra of W. The highest weight of S is
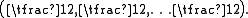
The Clifford action is not faithful on S: ClnC can be identified with End(S) ⊕ End(S′), where u acts with the opposite sign on S′. More precisely, the two representations are related by the parity involution α of ClnC (also known as the principal automorphism), which is the identity on the even subalgebra, and minus the identity on the odd part of ClnC. In other words, there is a linear isomorphism from S to S′, which identifies the action of A in ClnC on S with the action of α(A) on S′.
Bilinear forms
if λ is a weight of S, so is −λ. It follows that S is isomorphic to the dual representationDual representation
In mathematics, if G is a group and ρ is a linear representation of it on the vector space V, then the dual representation is defined over the dual vector space as follows:...
S∗.
When n = 2m+1 is odd, the isomorphism B: S → S∗ is unique up to scale by Schur's lemma
Schur's lemma
In mathematics, Schur's lemma is an elementary but extremely useful statement in representation theory of groups and algebras. In the group case it says that if M and N are two finite-dimensional irreducible representations...
, since S is irreducible, and it defines a nondegenerate invariant bilinear form β on S via
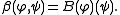
Here invariance means that
for all ξ in so(n,C) and φ, ψ in S — in other words the action of ξ is skew with respect to β. In fact, more is true: S∗ is a representation of the opposite
Opposite category
In category theory, a branch of mathematics, the opposite category or dual category Cop of a given category C is formed by reversing the morphisms, i.e. interchanging the source and target of each morphism. Doing the reversal twice yields the original category, so the opposite of an opposite...
Clifford algebra, and therefore, since ClnC only has two nontrivial simple module
Simple module
In mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
s S and S′, related by the parity involution α, there is an antiautomorphism τ of ClnC such that
for any A in ClnC. In fact τ is reversion (the antiautomorphism induced by the identity on V) for m even, and conjugation (the antiautomorphism induced by minus the identity on V) for m odd. These two antiautomorphisms are related by parity involution α, which is the automorphism induced by minus the identity on V. Both satisfy τ(ξ) = −ξ for ξ in so(n,C).
When n = 2m, the situation depends more sensitively upon the parity of m. For m even, a weight λ has an even number of minus signs if and only if −λ does; it follows that there are separate isomorphisms B±: S± → S±∗ of each half-spin representation with its dual, each determined uniquely up to scale. These may be combined into an isomorphism B: S → S∗. For m odd, λ is a weight of S+ if and only if −λ is a weight of S−; thus there is an isomorphism from S+ to S−∗, again unique up to scale, and its transpose provides an isomorphism from S− to S+∗. These may again be combined into an isomorphism B: S → S∗.
For both m even and m odd, the freedom in the choice of B may be restricted to an overall scale by insisting that the bilinear form β corresponding to B satisfies (1), where τ is a fixed antiautomorphism (either reversion or conjugation).
Symmetry and the tensor square
The symmetry properties of β: S ⊗ S → C can be determined using Clifford algebras or representation theory. In fact much more can be said: the tensor square S ⊗ S must decompose into a direct sum of k-forms on V for various k, because its weights are all elements in h∗ whose components belong to {−1,0,1}. Now equivariantEquivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
linear maps S ⊗ S → ∧kV∗ correspond bijectively to invariant maps ∧kV ⊗ S ⊗ S → C and nonzero such maps can be constructed via the inclusion of ∧kV into the Clifford algebra. Furthermore if β(φ,ψ) = ε β(ψ,φ) and τ has sign εk on ∧kV then
for A in ∧kV.
If n = 2m+1 is odd then it follows from Schur's Lemma that
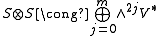
(both sides have dimension 22m and the representations on the right are inequivalent). Because the symmetries are governed by an involution τ that is either conjugation or reversion, the symmetry of the ∧2jV∗ component alternates with j. Elementary combinatorics gives
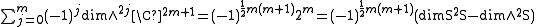
and the sign determines which representations occur in S2S and which occur in ∧2S. In particular
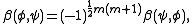and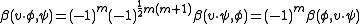for v ∈ V (which is isomorphic to ∧2mV), confirming that τ is reversion for m even, and conjugation for m odd.
If n=2m is even, then the analysis is more involved, but the result is a more refined decomposition: S2S±, ∧2S± and S+ ⊗ S− can each be decomposed as a direct sum of k-forms (where for k=m there is a further decomposition into selfdual and antiselfdual m-forms).
The main outcome is a realisation of so(n,C) as a subalgebra of a classical Lie algebra on S, depending upon n modulo 8, according to the following table:
| n mod 8 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| Spinor algebra |  |
 |
 |
 |
 |
 |
 |
 |
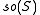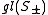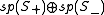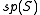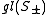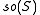For n ≤ 6, these embeddings are isomorphisms (onto sl rather than gl for n=6):
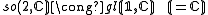
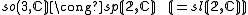
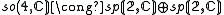
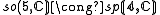
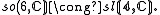
Real representations
The complex spin representations of so(n,C) yield real representations S of so(p,q) by restricting the action to the real subalgebras. However, there are additional "reality" structures that are invariant under the action of the real Lie algebras. These come in three types.- There is an invariant complex antilinear map r: S → S with r2 = idS. The fixed point set of r is then a real vector subspace SR of S with SR ⊗ C = S. This is called a real structure.
- There is an invariant complex antilinear map j: S → S with j2 = −idS. It follows that the triple i, j and k:=ij make S into a quaternionic vector space SH. This is called a quaternionic structure.
- There is an invariant complex antilinear map b: S → S∗ that is invertible. This defines a hermitian bilinear form on S and is called a hermitian structure.
The type of structure invariant under so(p,q) depends only on the signature p−q modulo 8, and is given by the following table.
| p−q mod 8 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| Structure | R + R | R | C | H | H + H | H | C | R |
Here R, C and H denote real, hermitian and quaternionic structures respectively, and R+R and H+H indicate that the half-spin representations both admit real or quaternionic structures respectively.
Description and tables
To complete the description of real representation, we must describe how these structures interact with the invariant bilinear forms. Since n = p+q ≅ p - q mod 2, there are two cases: the dimension and signature are both even, and the dimension and signature are both odd.The odd case is simpler, there is only one complex spin representation S, and hermitian structures do not occur. Apart from the trivial case n = 1, S is always even dimensional, say dim S = 2N. The real forms of so(2N,C) are so(K,L) with K + L = 2N and so*(N,H), while the real forms of sp(2N,C) are sp(2N,R) and sp(K,L) with K + L = N. The presence of a Clifford action of V on S forces K = L in both cases unless pq = 0, in which case KL=0, which is denoted simply so(2N) or sp(N). Hence the odd spin representations may be summarized in the following table.
| n mod 8 | 1, 7 | 3, 5 | |
|---|---|---|---|
| p-q mod 8 | so(2N,C) | sp(2N,C) | |
| 1, 7 | R | so(N,N) or so(2N) | sp(2N,R) |
| 3, 5 | H | so*(N,H) | sp(N/2,N/2)† or sp(N) |
(†) N is even for n>3 and for n=3, this is sp(1).
The even dimensional case is similar. For n>2, the complex half-spin representations are even dimensional. We have additionally to deal with hermitian structures and the real forms of sl(2N,C), which are sl(2N,R), su(K,L) with K + L = 2N, and sl(N,H). The resulting even spin representations are summarized as follows.
| n mod 8 | 0 | 2, 6 | 4 | |
|---|---|---|---|---|
| p-q mod 8 | so(2N,C)+so(2N,C) | sl(2N,C) | sp(2N,C)+sp(2N,C) | |
| 0 | R+R | so(N,N)+so(N,N)* | sl(2N,R) | sp(2N,R)+sp(2N,R) |
| 2, 6 | C | so(2N,C) | su(N,N) | sp(2N,C) |
| 4 | H+H | so*(N,H)+so*(N,H) | sl(N,H) | sp(N/2,N/2)+sp(N/2,N/2)† |
(*) For pq=0, we have instead so(2N)+so(2N)
(†) N is even for n>4 and for pq=0 (which includes n=4 with N=1), we have instead sp(N)+sp(N)
The low dimensional isomorphisms in the complex case have the following real forms.
| Euclidean signature | Minkowskian signature | Other signatures | |
 |
 |
||
 |
 |
||
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
 |
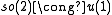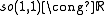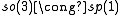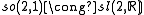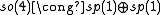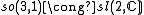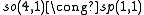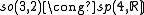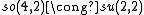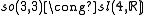The only special isomorphism of real Lie algebras missing from this table is