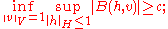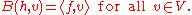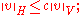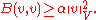Lions–Lax–Milgram theorem
Encyclopedia
In mathematics
, the Lions–Lax–Milgram theorem (or simply Lions’ theorem) is a result in functional analysis
with applications in the study of partial differential equation
s. It is a generalization of the famous Lax–Milgram theorem, which gives conditions under which a bilinear function can be "inverted" to show the existence and uniqueness of a weak solution
to a given boundary value problem
. The result is named after the mathematicians Jacques-Louis Lions
, Peter Lax
and Arthur Milgram
.
and V a normed space. Let B : H × V → R be a continuous
, bilinear function. Then the following are equivalent:
Suppose that V is continuously embedded
in H and that B is V-elliptic, i.e.
Then the above coercivity condition (and hence the existence result) holds.
in n spatial dimensions (x) and one time dimension (t):
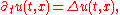
where Δ denotes the Laplace operator
. Two questions arise immediately: on what domain in spacetime
is the heat equation to be solved, and what boundary conditions are to be imposed? The first question — the shape of the domain — is the one in which the power of the Lions–Lax–Milgram theorem can be seen. In simple settings, it suffices to consider cylindrical domains: i.e., one fixes a spatial region of interest, Ω, and a maximal time, T ∈(0, +∞], and proceeds to solve the heat equation on the "cylinder"

One can then proceed to solve the heat equation using classical Lax–Milgram theory (and/or Galerkin approximations) on each "time slice" {t} × Ω. This is all very well if one only wishes to solve the heat equation on a domain that does not change its shape as a function of time. However, there are many applications for which this is not true: for example, if one wishes to solve the heat equation on the polar ice cap
, one must take account of the changing shape of the volume of ice as it evaporates and/or iceberg
s break away. In other words, one must at least be able to handle domains G in spacetime that do not look the same along each "time slice". (There is also the added complication of domains whose shape changes according to the solution u of the problem itself.) Such domains and boundary conditions are beyond the reach of classical Lax–Milgram theory, but can be attacked using Lions’ theorem.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Lions–Lax–Milgram theorem (or simply Lions’ theorem) is a result in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
with applications in the study of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s. It is a generalization of the famous Lax–Milgram theorem, which gives conditions under which a bilinear function can be "inverted" to show the existence and uniqueness of a weak solution
Weak solution
In mathematics, a weak solution to an ordinary or partial differential equation is a function for which the derivatives may not all exist but which is nonetheless deemed to satisfy the equation in some precisely defined sense. There are many different definitions of weak solution, appropriate for...
to a given boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
. The result is named after the mathematicians Jacques-Louis Lions
Jacques-Louis Lions
Jacques-Louis Lions ForMemRS was a French mathematician who made contributions to the theory of partial differential equations and to stochastic control, among other areas. He received the SIAM's John Von Neumann prize in 1986. Lions is listed as an ISI highly cited researcher.-Biography:After...
, Peter Lax
Peter Lax
Peter David Lax is a mathematician working in the areas of pure and applied mathematics. He has made important contributions to integrable systems, fluid dynamics and shock waves, solitonic physics, hyperbolic conservation laws, and mathematical and scientific computing, among other fields...
and Arthur Milgram
Arthur Milgram
Arthur Norton Milgram was an American mathematician. He made contributions in functional analysis, combinatorics, differential geometry, topology, partial differential equations, and Galois theory...
.
Statement of the theorem
Let H be a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
and V a normed space. Let B : H × V → R be a continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, bilinear function. Then the following are equivalent:
- (coercivityCoercive functionIn mathematics, a coercive function is a function that "grows rapidly" at the extremes of the space on which it is defined. More precisely, a function f : Rn → Rn is called coercive if...
) for some constant c > 0,
- (existence of a "weak inverse") for each continuous linear functional f ∈ V∗, there is an element h ∈ H such that
Related results
The Lions–Lax–Milgram theorem can be applied by using the following result, the hypotheses of which are quite common and easy to verify in practical applications:Suppose that V is continuously embedded
Continuously embedded
In mathematics, one normed vector space is said to be continuously embedded in another normed vector space if the inclusion function between them is continuous. In some sense, the two norms are "almost equivalent", even though they are not both defined on the same space...
in H and that B is V-elliptic, i.e.
- for some c > 0 and all v ∈ V,
- for some α > 0 and all v ∈ V,
Then the above coercivity condition (and hence the existence result) holds.
Importance and applications
Lions’ generalization is an important one since it allows one to tackle boundary value problems beyond the Hilbert space setting of the original Lax–Milgram theory. To illustrate the power of Lions' theorem, consider the heat equationHeat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
in n spatial dimensions (x) and one time dimension (t):
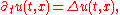
where Δ denotes the Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
. Two questions arise immediately: on what domain in spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
is the heat equation to be solved, and what boundary conditions are to be imposed? The first question — the shape of the domain — is the one in which the power of the Lions–Lax–Milgram theorem can be seen. In simple settings, it suffices to consider cylindrical domains: i.e., one fixes a spatial region of interest, Ω, and a maximal time, T ∈(0, +∞], and proceeds to solve the heat equation on the "cylinder"

One can then proceed to solve the heat equation using classical Lax–Milgram theory (and/or Galerkin approximations) on each "time slice" {t} × Ω. This is all very well if one only wishes to solve the heat equation on a domain that does not change its shape as a function of time. However, there are many applications for which this is not true: for example, if one wishes to solve the heat equation on the polar ice cap
Polar ice cap
A polar ice cap is a high latitude region of a planet or natural satellite that is covered in ice. There are no requirements with respect to size or composition for a body of ice to be termed a polar ice cap, nor any geological requirement for it to be over land; only that it must be a body of...
, one must take account of the changing shape of the volume of ice as it evaporates and/or iceberg
Iceberg
An iceberg is a large piece of ice from freshwater that has broken off from a snow-formed glacier or ice shelf and is floating in open water. It may subsequently become frozen into pack ice...
s break away. In other words, one must at least be able to handle domains G in spacetime that do not look the same along each "time slice". (There is also the added complication of domains whose shape changes according to the solution u of the problem itself.) Such domains and boundary conditions are beyond the reach of classical Lax–Milgram theory, but can be attacked using Lions’ theorem.