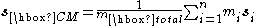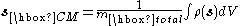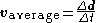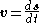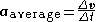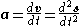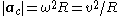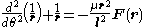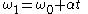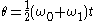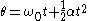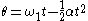List of equations in classical mechanics
Encyclopedia
Classical mechanics is the branch of physics
used to describe the motion of macroscopic
objects. It is the most familiar of the theories of physics. The concepts it covers, such as mass
, acceleration
, and force
, are commonly used and known. The subject is based upon a three-dimensional
Euclidean space
with fixed axes, called a frame of reference. The point of concurrency
of the three axes is known as the origin of the particular space.
Classical mechanics utilises many equation
s—as well as other mathematical
concepts—which relate various physical quantities to one another. These include differential equations, manifold
s, Lie group
s, and ergodic theory
. This page gives a summary of the most important of these.
Name of equation
average velocity = change in distance / change in time
(R = radius of the circle, ω = v/R angular velocity
)
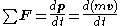
(Constant Mass)
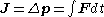
Moment of inertia
For a single axis of rotation:
The moment of inertia for an object is the sum of the products of the mass element and the square of their distances from the axis of rotation:
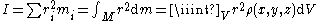
Angular momentum
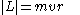if v is perpendicular to r
Vector form:
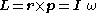
(Note: I can be treated like a vector if it is diagonalized first, but it is actually a 3×3 matrix - a tensor
of rank-2)
r is the radius vector.
Torque
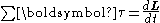
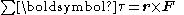
if |r| and the sine of the angle between r and p remains constant.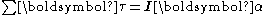
This one is very limited, more added later. α = dω/dt
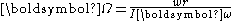
(Note: w is the weight of the spinning flywheel)
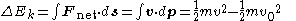
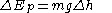in field of gravity
must be used.
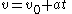
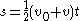
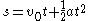
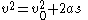
These equations can be adapted for angular motion, where angular acceleration is constant:
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
used to describe the motion of macroscopic
Macroscopic
The macroscopic scale is the length scale on which objects or processes are of a size which is measurable and observable by the naked eye.When applied to phenomena and abstract objects, the macroscopic scale describes existence in the world as we perceive it, often in contrast to experiences or...
objects. It is the most familiar of the theories of physics. The concepts it covers, such as mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
, acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
, and force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
, are commonly used and known. The subject is based upon a three-dimensional
Three-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
with fixed axes, called a frame of reference. The point of concurrency
Concurrent lines
In geometry, two or more lines are said to be concurrent if they intersect at a single point.In a triangle, four basic types of sets of concurrent lines are altitudes, angle bisectors, medians, and perpendicular bisectors:...
of the three axes is known as the origin of the particular space.
Classical mechanics utilises many equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
s—as well as other mathematical
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
concepts—which relate various physical quantities to one another. These include differential equations, manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s, Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s, and ergodic theory
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
. This page gives a summary of the most important of these.
Equations
| Equation | Year derived | Derived by | Notes | |
|---|---|---|---|---|
| Center of mass Center of mass In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body... |
Discrete case:
where n is the number of mass particles. Continuous case: where ρ(s) is the scalar mass density as a function of the position vector |
1687 | Isaac Newton Isaac Newton Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."... |
Velocity
average velocity = change in distance / change in time
Acceleration
- Centripetal Acceleration
(R = radius of the circle, ω = v/R angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
)
Force
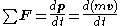
(Constant Mass)Impulse
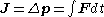
- if F is constant
Moment of inertiaMoment of inertiaIn classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
For a single axis of rotation:The moment of inertia for an object is the sum of the products of the mass element and the square of their distances from the axis of rotation:
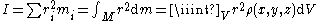
Angular momentumAngular momentumIn physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
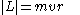if v is perpendicular to rVector form:
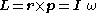
(Note: I can be treated like a vector if it is diagonalized first, but it is actually a 3×3 matrix - a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
of rank-2)
r is the radius vector.
TorqueTorqueTorque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
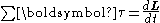
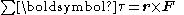
if |r| and the sine of the angle between r and p remains constant.
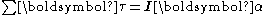
This one is very limited, more added later. α = dω/dt
Precession
Omega is called the precession angular speed, and is defined: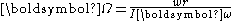(Note: w is the weight of the spinning flywheel)
Energy
for m as a constant: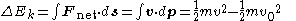 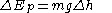in field of gravityCentral force motion
Equations of motion (constant acceleration)
These equations can be used only when acceleration is constant. If acceleration is not constant then calculusCalculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
must be used.
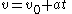
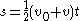
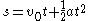
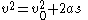
These equations can be adapted for angular motion, where angular acceleration is constant:
See also
- AcousticsAcousticsAcoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
- Classical mechanicsClassical mechanicsIn physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
- ElectromagnetismElectromagnetismElectromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
- MechanicsMechanicsMechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
- OpticsOpticsOptics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
- ThermodynamicsThermodynamicsThermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...