Littelmann path model
Encyclopedia
In mathematics
, the Littelmann path model is a combinatorial device
due to Peter Littelmann for computing multiplicities without overcounting in the representation theory
of symmetrisable Kac-Moody algebras. Its most important application is to complex semisimple Lie algebras or equivalently compact semisimple Lie groups, the case described in this article. Multiplicities in irreducible representations
, tensor products and branching rules can be calculated using a coloured directed graph
, with labels given by the simple roots
of the Lie algebra.
Developed as a bridge between the theory of crystal bases arising from the work of Kashiwara
and Lusztig on quantum group
s and the standard monomial theory of C. S. Seshadri
and Lakshmibai, Littelmann's path model associates to each irreducible representation a rational vector space with basis given by paths from the origin to a weight as well as a pair of root operators acting on paths for each simple root. This gives a direct way of recovering the algebraic and combinatorial structures previously discovered by Kashiwara and Lustzig using quantum groups.
include:
(Note that the first problem, of weight multiplicities, is the special case of the third in which the parabolic subalgebra is a Borel subalgebra. Moreover, the Levi branching problem can be embedded in the tensor product problem as a certain limiting case.)
Answers to these questions were first provided by Hermann Weyl and Richard Brauer
as consequences of explicit character formulas
, followed by later combinatorial formulas of Hans Freudenthal
, Robert Steinberg
and Bertram Kostant
; see . An unsatisfactory feature of these formulas is that they involved alternating sums for quantities that were known a priori to be non-negative. Littelmann's method expresses these multiplicities as sums of non-negative integers without overcounting. His work generalizes classical results based on Young tableau
x for the general linear Lie algebra
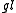n or the special linear Lie algebra
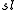n:
Attempts at finding similar algorithms without overcounting for the other classical Lie algebras had only been partially successful.
Littlemann's contribution was to give a unified combinatorial model that applied to all symmetrizable Kac-Moody algebras and provided explicit subtraction-free combinatorial formulas for weight multiplicities, tensor product rules and branching rules. He accomplished this by introducing the vector space V over Q generated by the weight lattice of a Cartan subalgebra; on the vector space of piecewise-linear paths in V connecting the origin to a weight, he defined a pair of root operators for each simple root of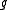
.
The combinatorial data could be encoded in a coloured directed graph, with labels given by the simple roots.
Littelmann's main motivation was to reconcile two different aspects of representation theory:
Although differently defined, the crystal basis, its root operators and crystal graph were later shown to be equivalent to Littelmann's path model and graph; see . In the case of complex semisimple Lie algebras, there is a simplified self-contained account in relying only on the properties of root system
s; this approach is followed here.
.
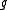A Littelmann path is a piecewise-linear mapping
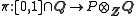
such that π(0) = 0 and π(1) is a weight.
Let (H α) be the basis of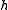
consisting of "coroot" vectors, dual to basis of 
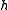* formed by simple roots
(α). For fixed α and a path π, the function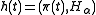
has a minimum value M.
Define non-decreasing self-mappings l and r of [0,1]
Q by
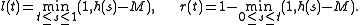
Thus l(t) = 0 until the last time that h(s) = M and r(t) = 1 after the first time that h(s) = M.
Define new paths πl and πr by
The root operators eα and fα are defined on a basis vector [π] by
The key feature here is that the paths form a basis for the root operators like that of a monomial representation
: when a root operator is applied to the basis element for a path, the result is either 0 or the basis element for another path.
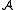be the algebra generated by the root operators. Let π(t) be a path lying wholly within the positive Weyl chamber defined by the simple roots. Using results on the path model of C. S. Seshadri
and Lakshmibai, Littelmann showed that
There is also an action of the Weyl group
on paths [π]. If α is a simple root and k = h(1), with h as above, then the corresponding reflection sα acts as follows:
If π is a path lying wholly inside the positive Weyl chamber, the Littelmann graph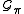
is defined to be the coloured, directed graph having as vertices the non-zero paths obtained by successively applying the operators fα to π. There is a directed arrow from one path to another labelled by the simple root α, if the target path is obtained from the source path by applying fα.
The Littelmann graph therefore only depends on λ. Kashiwara and Joseph proved that it coincides with the "crystal graph" defined by Kashiwara in the theory of crystal bases.
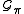with σ(1) = μ.
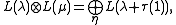
where τ ranges over paths in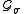
such that π 
τ lies entirely in the positive Weyl chamber and
the concatenation π
τ (t) is defined as π(2t) for t ≤ 1/2 and π(1) + τ( 2t – 1) for t ≥ 1/2.
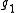is the Levi component of a parabolic subalgebra of 
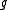with weight lattice P1 
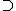P then
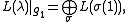
where the sum ranges over all paths σ in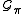
which lie wholly in the positive Weyl chamber for 
.
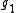Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Littelmann path model is a combinatorial device
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
due to Peter Littelmann for computing multiplicities without overcounting in the representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of symmetrisable Kac-Moody algebras. Its most important application is to complex semisimple Lie algebras or equivalently compact semisimple Lie groups, the case described in this article. Multiplicities in irreducible representations
Weyl character formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by ....
, tensor products and branching rules can be calculated using a coloured directed graph
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, with labels given by the simple roots
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
of the Lie algebra.
Developed as a bridge between the theory of crystal bases arising from the work of Kashiwara
Masaki Kashiwara
is a Japanese mathematician. He was a student of Mikio Sato at the University of Tokyo. Sato and Kashiwara have collaborated on algebraic analysis and D-module theory.He is a member of the French Academy of Sciences.- Concepts named after Kashiwara :...
and Lusztig on quantum group
Quantum group
In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
s and the standard monomial theory of C. S. Seshadri
C. S. Seshadri
C.S.Seshadri FRS is an eminent Indian mathematician. He is currently Director-Emeritus of the Chennai Mathematical Institute, and is known for his work in algebraic geometry. The Seshadri constant is named after him. He is also a recipient of the prestigious Padma Bhushan in 2009, the third highest...
and Lakshmibai, Littelmann's path model associates to each irreducible representation a rational vector space with basis given by paths from the origin to a weight as well as a pair of root operators acting on paths for each simple root. This gives a direct way of recovering the algebraic and combinatorial structures previously discovered by Kashiwara and Lustzig using quantum groups.
Background and motivation
Some of the basic questions in the representation theory of complex semisimple Lie algebras or compact semisimple Lie groups going back to Hermann WeylHermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
include:
- For a given dominant weight λ, find the weight multiplicities in the irreducible representationWeyl character formulaIn mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by ....
L(λ) with highest weight λ. - For two highest weights λ, μ, find the decomposition of their tensor product L(λ)
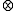L(μ) into irreducible representations. - Suppose that
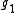is the Levi componentLevi decompositionIn Lie theory and representation theory, the Levi decomposition, conjectured by Killing and Cartan and proved by , states that any finite dimensional real Lie algebra g is the semidirect product of a solvable ideal and a semisimple subalgebra....
of a parabolic subalgebra of a semisimple Lie algebra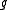
. For a given dominant highest weight λ, determine the branching rule for decomposing the restriction of L(λ) to 
.
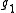(Note that the first problem, of weight multiplicities, is the special case of the third in which the parabolic subalgebra is a Borel subalgebra. Moreover, the Levi branching problem can be embedded in the tensor product problem as a certain limiting case.)
Answers to these questions were first provided by Hermann Weyl and Richard Brauer
Richard Brauer
Richard Dagobert Brauer was a leading German and American mathematician. He worked mainly in abstract algebra, but made important contributions to number theory...
as consequences of explicit character formulas
Weyl character formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by ....
, followed by later combinatorial formulas of Hans Freudenthal
Hans Freudenthal
Hans Freudenthal was a Dutch mathematician. He made substantial contributions to algebraic topology and also took an interest in literature, philosophy, history and mathematics education....
, Robert Steinberg
Robert Steinberg
Robert Steinberg is a mathematician at the University of California, Los Angeles who invented the Steinberg representation, the Steinberg group in algebraic K-theory, and the Steinberg groups in Lie theory that yield finite simple groups over finite fields. He received his Ph.D...
and Bertram Kostant
Bertram Kostant
-Early life and education:Kostant grew up in New York City, where he graduated from the celebrated Stuyvesant High School in 1945. He went on to obtain an undergraduate degree in mathematics from Purdue University in 1950. He earned his Ph.D...
; see . An unsatisfactory feature of these formulas is that they involved alternating sums for quantities that were known a priori to be non-negative. Littelmann's method expresses these multiplicities as sums of non-negative integers without overcounting. His work generalizes classical results based on Young tableau
Young tableau
In mathematics, a Young tableau is a combinatorial object useful in representation theory. It provides a convenient way to describe the group representations of the symmetric and general linear groups and to study their properties. Young tableaux were introduced by Alfred Young, a mathematician at...
x for the general linear Lie algebra
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
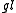n or the special linear Lie algebraSpecial linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversio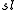n....
n:- Issai SchurIssai SchurIssai Schur was a mathematician who worked in Germany for most of his life. He studied at Berlin...
's result in his 1901 dissertation that the weight multiplicities could be counted in terms of column-strict Young tableaux (i.e. weakly increasing to the right along rows, and strictly increasing down columns). - The celebrated Littlewood-Richardson rule that describes both tensor product decompositions and branching from
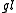m+n to 
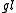m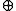 
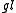n in terms of lattice permutations of skew tableaux.
Attempts at finding similar algorithms without overcounting for the other classical Lie algebras had only been partially successful.
Littlemann's contribution was to give a unified combinatorial model that applied to all symmetrizable Kac-Moody algebras and provided explicit subtraction-free combinatorial formulas for weight multiplicities, tensor product rules and branching rules. He accomplished this by introducing the vector space V over Q generated by the weight lattice of a Cartan subalgebra; on the vector space of piecewise-linear paths in V connecting the origin to a weight, he defined a pair of root operators for each simple root of
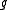.The combinatorial data could be encoded in a coloured directed graph, with labels given by the simple roots.
Littelmann's main motivation was to reconcile two different aspects of representation theory:
- The standard monomial theory of Lakshmibai and Seshadri arising from the geometry of Schubert varietiesSchubert varietyIn algebraic geometry, a Schubert variety is a certain subvariety of a Grassmannian, usually with singular points. Described by means of linear algebra, a typical example consists of the k-dimensional subspaces V of an n dimensional vector space W, such that\dim\ge jfor j = 1, 2, ..., k,...
. - Crystal bases arising in the approach to quantum groupQuantum groupIn mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
s of Masaki KashiwaraMasaki Kashiwarais a Japanese mathematician. He was a student of Mikio Sato at the University of Tokyo. Sato and Kashiwara have collaborated on algebraic analysis and D-module theory.He is a member of the French Academy of Sciences.- Concepts named after Kashiwara :...
and George Lusztig. Kashiwara and Lusztig constructed canonical bases for representations of deformations of the universal enveloping algebraUniversal enveloping algebraIn mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
of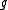
depending on a formal deformation parameter q. In the degenerate case when q = 0, these yield crystal bases together with pairs of operators corresponding to simple roots; see .
Although differently defined, the crystal basis, its root operators and crystal graph were later shown to be equivalent to Littelmann's path model and graph; see . In the case of complex semisimple Lie algebras, there is a simplified self-contained account in relying only on the properties of root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
s; this approach is followed here.
Definitions
Let P be the weight lattice in the dual of a Cartan subalgebra of the semisimple Lie algebra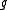.A Littelmann path is a piecewise-linear mapping
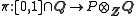
such that π(0) = 0 and π(1) is a weight.
Let (H α) be the basis of
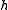consisting of "coroot" vectors, dual to basis of 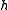* formed by simple rootsRoot system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
(α). For fixed α and a path π, the function
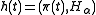has a minimum value M.Define non-decreasing self-mappings l and r of [0,1]
Q by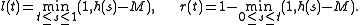Thus l(t) = 0 until the last time that h(s) = M and r(t) = 1 after the first time that h(s) = M.
Define new paths πl and πr by
The root operators eα and fα are defined on a basis vector [π] by
-
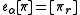if r (0) = 0 and 0 otherwise;
-
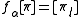if l (1) = 1 and 0 otherwise.
The key feature here is that the paths form a basis for the root operators like that of a monomial representation
Monomial representation
In mathematics, a linear representation ρ of a group G is a monomial representation if there is a finite-index subgroup H and a one-dimensional linear representation σ of H, such that ρ is equivalent to the induced representation...
: when a root operator is applied to the basis element for a path, the result is either 0 or the basis element for another path.
Properties
Let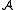 be the algebra generated by the root operators. Let π(t) be a path lying wholly within the positive Weyl chamber defined by the simple roots. Using results on the path model of C. S. SeshadriC. S. Seshadri
C.S.Seshadri FRS is an eminent Indian mathematician. He is currently Director-Emeritus of the Chennai Mathematical Institute, and is known for his work in algebraic geometry. The Seshadri constant is named after him. He is also a recipient of the prestigious Padma Bhushan in 2009, the third highest...
and Lakshmibai, Littelmann showed that
- the
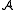-module generated by [π] depends only on π(1) = λ and has a Q-basis consisting of paths [σ]; - the multiplicity of the weight μ in the integrable highest weight representation L(λ) is the number of paths σ with σ(1) = μ.
There is also an action of the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
on paths [π]. If α is a simple root and k = h(1), with h as above, then the corresponding reflection sα acts as follows:
- sα [π] = [π] if k = 0;
- sα [π]= fαk [π] if k > 0;
- sα [π]= eα – k [π] if k > 0.
If π is a path lying wholly inside the positive Weyl chamber, the Littelmann graph
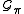is defined to be the coloured, directed graph having as vertices the non-zero paths obtained by successively applying the operators fα to π. There is a directed arrow from one path to another labelled by the simple root α, if the target path is obtained from the source path by applying fα.- The Littelmann graphs of two paths are isomorphic as coloured, directed graphs if and only if the paths have the same end point.
The Littelmann graph therefore only depends on λ. Kashiwara and Joseph proved that it coincides with the "crystal graph" defined by Kashiwara in the theory of crystal bases.
Character formula
If π(1) = λ, the multiplicity of the weight μ in L(λ) is the number of paths from π to vertices σ in the Littelmann graph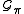 with σ(1) = μ.Generalized Littlewood-Richardson rule
Let π and σ be paths in the positive Weyl chamber with π(1) = λ and σ(1) = μ. Then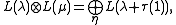where τ ranges over paths in
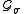such that π τ lies entirely in the positive Weyl chamber andthe concatenation π
τ (t) is defined as π(2t) for t ≤ 1/2 and π(1) + τ( 2t – 1) for t ≥ 1/2.Branching rule
If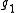 is the Levi component of a parabolic subalgebra of 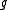with weight lattice P1 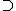P then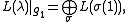where the sum ranges over all paths σ in
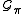which lie wholly in the positive Weyl chamber for .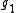