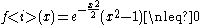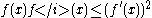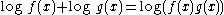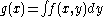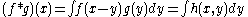Logarithmically concave function
Encyclopedia
In convex analysis
, a non-negative function is logarithmically concave (or log-concave for short) if its domain is a convex set
, and if it satisfies the inequality
Convex analysis
Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory....
, a non-negative function is logarithmically concave (or log-concave for short) if its domain is a convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
, and if it satisfies the inequality
-
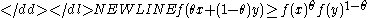
for all and . If is strictly positive, this is equivalent to saying that the logarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of the function, , is concaveConcave functionIn mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:...
; that is,-
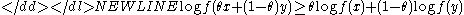
for all and .
Examples of log-concave functions are the 0-1 indicator functions of convex sets (which requires the more flexible definition), and the Gaussian function.
Similarly, a function is log-convex if satisfies the reverse inequality-
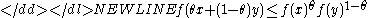
for all and .
Properties
- A positive log-concave function is also quasi-concave.
- Every concave function that is nonnegative on its domain is log-concave. However, the reverse does not necessarily hold. An example is the Gaussian function = which is log-concave since = is a concave function of . But is not concave since the second derivative is positive for || > 1:
- A twice differentiable, nonnegative function with a convex domain is log-concave if and only if for all satisfying ,
-
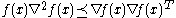 ,
,
- i.e.
-
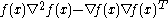 is
is
- negative semi-definitePositive-definite matrixIn linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
. For functions of one variable, this condition simplifies to
Operations preserving log-concavity
- Products: The product of log-concave functions is also log-concave. Indeed, if and are log-concave functions, then and are concave by definition. Therefore
- is concave, and hence also is log-concave.
- MarginalsMarginal distributionIn probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. The term marginal variable is used to refer to those variables in the subset of variables being retained...
: if : is log-concave, then
- is log-concave (see Prékopa–Leindler inequality).
- This implies that convolutionConvolutionIn mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
preserves log-concavity, since is log-concave if and are log-concave, and therefore
- is log-concave.
See also
- logarithmically convex functionLogarithmically convex functionIn mathematics, a function f defined on a convex subset of a real vector space and taking positive values is said to be logarithmically convex if \log f is a convex function of x....
- convex functionConvex functionIn mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
- logarithmically concave measureLogarithmically concave measureIn mathematics, a Borel measure μ on n-dimensional Euclidean space Rn is called logarithmically concave if, for any compact subsets A and B of Rn and 0 < λ < 1, one haswhere λ A + B denotes the Minkowski sum...
-
-