
Lucas–Lehmer test
Encyclopedia
In computational number theory
, the Lucas test is a primality test
for a natural number n; it requires that the prime factors of n − 1 be already known. It is the basis of the Pratt certificate that gives a concise verification that n is prime.
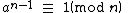
and for every prime factor q of n − 1
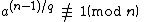
then n is prime. If no such number a exists, then n is composite
.
The reason for the correctness of this claim is as follows: if the first equality holds for a, we can deduce that a and n are coprime. If a also survives the second step, then the order
of a in the group
(Z/nZ)* is equal to n−1, which means that the order of that group is n−1 (because the order of every element of a group divides the order of the group), implying that n is prime
. Conversely, if n is prime, then there exists a primitive root modulo n
, or generator
of the group (Z/nZ)*. Such a generator has order |(Z/nZ)*| = n−1 and both equalities will hold for any such primitive root.
Note that if there exists an a < n such that the first equality fails, a is called a Fermat witness for the compositeness of n.
We randomly select an a < n of 17. Now we compute:
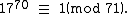
For all integers a it is known that
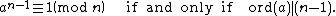
Therefore, the multiplicative order of 17 (mod 71) is not necessarily 70 because some factor of 70 may also work above. So check 70 divided by its prime factors:
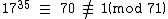
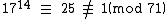
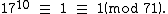
Unfortunately, we get that 1710≡1 (mod 71). So we still don't know if 71 is prime or not.
We try another random a, this time choosing a = 11. Now we compute:
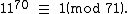
Again, this does not show that the multiplicative order of 11 (mod 71) is 70 because some factor of 70 may also work. So check 70 divided by its prime factors:
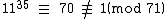
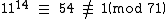
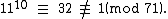
So the multiplicative order of 11 (mod 71) is 70, and thus 71 is prime.
(To carry out these modular exponentiation
s, one could use a fast exponentiation algorithm like binary
or addition-chain exponentiation
).
as follows:
Input: n > 2, an odd integer to be tested for primality; k, a parameter that determines the accuracy of the test
Output: prime if n is prime, otherwise composite or possibly composite;
determine the prime factors of n−1.
LOOP1: repeat k times:
pick a randomly in the range [2, n − 1]
if an-1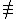 1 (mod n) then return composite
1 (mod n) then return composite
otherwise
LOOP2: for all prime factors q of n−1:
if a(n-1)/q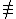 1 (mod n)
1 (mod n)
if we did not check this equality for all prime factors of n−1
then do next LOOP2
otherwise return prime
otherwise do next LOOP1
return possibly composite.
Computational number theory
In mathematics, computational number theory, also known as algorithmic number theory, is the study of algorithms for performing number theoretic computations...
, the Lucas test is a primality test
Primality test
A primality test is an algorithm for determining whether an input number is prime. Amongst other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not...
for a natural number n; it requires that the prime factors of n − 1 be already known. It is the basis of the Pratt certificate that gives a concise verification that n is prime.
Concepts
Let n be a positive integer. If there exists an integer 1 < a < n such that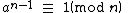
and for every prime factor q of n − 1
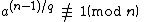
then n is prime. If no such number a exists, then n is composite
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
.
The reason for the correctness of this claim is as follows: if the first equality holds for a, we can deduce that a and n are coprime. If a also survives the second step, then the order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
of a in the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
(Z/nZ)* is equal to n−1, which means that the order of that group is n−1 (because the order of every element of a group divides the order of the group), implying that n is prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. Conversely, if n is prime, then there exists a primitive root modulo n
Primitive root modulo n
In modular arithmetic, a branch of number theory, a primitive root modulo n is any number g with the property that any number coprime to n is congruent to a power of g modulo n. In other words, g is a generator of the multiplicative group of integers modulo n...
, or generator
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
of the group (Z/nZ)*. Such a generator has order |(Z/nZ)*| = n−1 and both equalities will hold for any such primitive root.
Note that if there exists an a < n such that the first equality fails, a is called a Fermat witness for the compositeness of n.
Example
For example, take n = 71. Then n − 1 = 70 and the prime factors of 70 are 2, 5 and 7.We randomly select an a < n of 17. Now we compute:
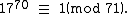
For all integers a it is known that
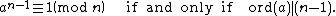
Therefore, the multiplicative order of 17 (mod 71) is not necessarily 70 because some factor of 70 may also work above. So check 70 divided by its prime factors:
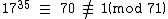
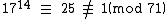
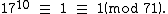
Unfortunately, we get that 1710≡1 (mod 71). So we still don't know if 71 is prime or not.
We try another random a, this time choosing a = 11. Now we compute:
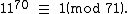
Again, this does not show that the multiplicative order of 11 (mod 71) is 70 because some factor of 70 may also work. So check 70 divided by its prime factors:
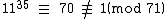
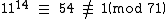
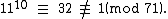
So the multiplicative order of 11 (mod 71) is 70, and thus 71 is prime.
(To carry out these modular exponentiation
Modular exponentiation
Modular exponentiation is a type of exponentiation performed over a modulus. It is particularly useful in computer science, especially in the field of cryptography....
s, one could use a fast exponentiation algorithm like binary
Exponentiation by squaring
Exponentiating by squaring is a general method for fast computation of large integer powers of a number. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. In additive notation the appropriate term is double-and-add...
or addition-chain exponentiation
Addition-chain exponentiation
In mathematics and computer science, optimal addition-chain exponentiation is a method of exponentiation by positive integer powers that requires a minimal number of multiplications. It works by creating a shortest addition chain that generates the desired exponent. Each exponentiation in the chain...
).
Algorithm
The algorithm can be written in pseudocodePseudocode
In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...
as follows:
Input: n > 2, an odd integer to be tested for primality; k, a parameter that determines the accuracy of the test
Output: prime if n is prime, otherwise composite or possibly composite;
determine the prime factors of n−1.
LOOP1: repeat k times:
pick a randomly in the range [2, n − 1]
if an-1
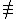 1 (mod n) then return composite
1 (mod n) then return compositeotherwise
LOOP2: for all prime factors q of n−1:
if a(n-1)/q
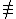 1 (mod n)
1 (mod n)if we did not check this equality for all prime factors of n−1
then do next LOOP2
otherwise return prime
otherwise do next LOOP1
return possibly composite.

