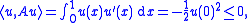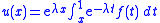Lumer-Phillips theorem - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the Lumer–Phillips theorem, named after Günter Lumer and Ralph Phillips, is a result in the theory of strongly continuous semigroups that gives a necessary and sufficient condition for a linear operator in a Banach space

Banach space

In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...

to generate a contraction semigroup.

Statement of the theorem

Let A be a linear operator defined on a linear subspace D(A) of the Banach space

Banach space

X. Then A generates a contraction semigroup if and only if

D(A) is dense in X,
A is closed
Closed operator
In mathematics, specifically in functional analysis, closed linear operators are an important class of linear operators on Banach spaces. They are more general than bounded operators, and therefore not necessarily continuous, but they still retain nice enough properties that one can define the...

,
A is dissipative, and
A − λ₀I is surjective for some λ₀> 0, where I denotes the identity operator.

Reflexive spaces

Let A be a linear operator defined on a linear subspace D(A) of the reflexive

Reflexive space

In functional analysis, a Banach space is called reflexive if it coincides with the dual of its dual space in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.- Normed spaces :Suppose X is a normed vector space over R or C...

Banach space

X. Then A generates a contraction semigroup if and only if

A is dissipative, and
A − λ₀I is surjective for some λ₀> 0, where I denotes the identity operator.

Note that the conditions that D(A) is dense and that A is closed are dropped in comparison to the non-reflexive case. This is because in the reflexive case they follow from the other two conditions.

Dissipativity of the adjoint

Let A be a linear operator defined on a dense linear subspace D(A) of the reflexive

Reflexive space

Banach space

X. Then A generates a contraction semigroup if and only if

A is closed
Closed operator
In mathematics, specifically in functional analysis, closed linear operators are an important class of linear operators on Banach spaces. They are more general than bounded operators, and therefore not necessarily continuous, but they still retain nice enough properties that one can define the...

and both A and its adjoint operator A^∗ are dissipative.

In case that X is not reflexive, then this condition for A to generate a contraction semigroup is still sufficient, but not necessary.

Quasicontraction semigroups

Let A be a linear operator defined on a linear subspace D(A) of the Banach space

Banach space

X. Then A generates a quasi contraction semigroup if and only if

D(A) is dense in X,
A is closed
Closed operator
In mathematics, specifically in functional analysis, closed linear operators are an important class of linear operators on Banach spaces. They are more general than bounded operators, and therefore not necessarily continuous, but they still retain nice enough properties that one can define the...

,
A is quasidissipative, i.e. there exists a ω ≥ 0 such that ωI − A is dissipative operator, and
A − λ₀I is surjective for some λ₀ > ω, where I denotes the identity operator.

Examples

Consider H = L²([0, 1]; R) with its usual inner product, and let Au = u′ with domain D(A) equal to those functions u in the Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...

H¹([0, 1]; R) with u(1) = 0. D(A) is dense. Moreover, for every u in D(A),

so that A is dissipative. The ordinary differential equation u' − λu = f, u(1) = 0 has a unique solution u in H¹([0, 1]; R) for any f in L²([0, 1]; R), namely

so that the surjectivity condition is satisfied. Hence, by the reflexive version of the Lumer–Phillips theorem A generates a contraction semigroup.

There are many more examples where a direct application of the Lumer–Phillips theorem gives the desired result.

In conjunction with translation, scaling and perturbation theory the Lumer–Phillips theorem is the main tool for showing that certain operators generate strongly continuous semigroups. The following is an example in point.

A normal operator
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....

(an operator that commutes with its adjoint) on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...

generates a strongly continuous semigroup if and only if its spectrum
Spectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...

is bounded from above.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.