Mahler volume
Encyclopedia
In convex geometry
, the Mahler volume of a centrally symmetric convex body
is a dimensionless quantity
that is associated with the body and is invariant under linear transformation
s. It is named after German-English mathematician Kurt Mahler
. It is known that the shapes with the largest possible Mahler volume are the spheres and ellipsoids; this is now known as the Blaschke–Santaló inequality. The still-unsolved Mahler conjecture states that the minimum possible Mahler volume is attained by a hypercube
.
is defined as a compact
convex set with non-empty interior. If B is a centrally symmetric convex body in n-dimensional Euclidean space
, the polar body Bo is another centrally symmetric body in the same space, defined as the set
The Mahler volume of B is the product of the volumes of B and Bo.
If T is a linear transformation, then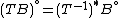
; thus applying T to B changes its volume by 
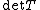and changes the volume of Bo by 
. Thus the overall Mahler volume of B is preserved by linear transformations.
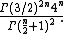
Here Γ represents the Gamma function
.
By affine invariance, any ellipsoid has the same Mahler volume.
The polar body of a polyhedron
or polytope
is its dual polyhedron
or dual polytope. In particular, the polar body of a cube
or hypercube
is an octahedron
or cross polytope. Its Mahler volume can be calculated as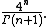
The Mahler volume of the sphere is larger than the Mahler volume of the hypercube by a factor of approximately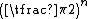
.
; the full result was proven much later by using a technique known as Steiner symmetrization by which any centrally symmetric convex body can be replaced with a more sphere-like body without decreasing its Mahler volume.
The shapes with the minimum known Mahler volume are hypercube
s, cross polytopes, and their Cartesian product
s and affine transformations. The Mahler conjecture states that the Mahler volume of these shapes is the smallest of any n-dimensional symmetric convex body; it remains unsolved. As Terry Tao
writes:
prove that the Mahler volume is bounded below by cn times the volume of a sphere for some absolute constant c > 0, matching the scaling behavior of the hypercube volume but with a smaller constant. A result of this type is known as an inverse Santaló inequality.
Convex geometry
Convex geometry is the branch of geometry studying convex sets, mainly in Euclidean space.Convex sets occur naturally in many areas of mathematics: computational geometry, convex analysis, discrete geometry, functional analysis, geometry of numbers, integral geometry, linear programming,...
, the Mahler volume of a centrally symmetric convex body
Convex body
In mathematics, a convex body in n-dimensional Euclidean space Rn is a compact convex set with non-empty interior.A convex body K is called symmetric if it is centrally symmetric with respect to the origin, i.e. a point x lies in K if and only if its antipode, −x, also lies in K...
is a dimensionless quantity
Dimensionless quantity
In dimensional analysis, a dimensionless quantity or quantity of dimension one is a quantity without an associated physical dimension. It is thus a "pure" number, and as such always has a dimension of 1. Dimensionless quantities are widely used in mathematics, physics, engineering, economics, and...
that is associated with the body and is invariant under linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s. It is named after German-English mathematician Kurt Mahler
Kurt Mahler
Kurt Mahler was a mathematician and Fellow of the Royal Society.He was a student at the universities in Frankfurt and Göttingen, graduating with a Ph.D...
. It is known that the shapes with the largest possible Mahler volume are the spheres and ellipsoids; this is now known as the Blaschke–Santaló inequality. The still-unsolved Mahler conjecture states that the minimum possible Mahler volume is attained by a hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
.
Definition
A convex body is Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
is defined as a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
convex set with non-empty interior. If B is a centrally symmetric convex body in n-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, the polar body Bo is another centrally symmetric body in the same space, defined as the set
The Mahler volume of B is the product of the volumes of B and Bo.
If T is a linear transformation, then
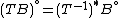; thus applying T to B changes its volume by 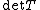and changes the volume of Bo by . Thus the overall Mahler volume of B is preserved by linear transformations.Examples
The polar body of an n-dimensional unit sphere is itself another unit sphere. Thus, its Mahler volume is just the square of its volume,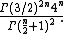Here Γ represents the Gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
.
By affine invariance, any ellipsoid has the same Mahler volume.
The polar body of a polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
or polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
is its dual polyhedron
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
or dual polytope. In particular, the polar body of a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
or hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
is an octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
or cross polytope. Its Mahler volume can be calculated as
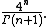
The Mahler volume of the sphere is larger than the Mahler volume of the hypercube by a factor of approximately
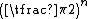.Extreme shapes
The Blaschke–Santaló inequality states that the shapes with maximum Mahler volume are the spheres and ellipsoids. The three-dimensional case of this result was proven by Wilhelm BlaschkeWilhelm Blaschke
Wilhelm Johann Eugen Blaschke was an Austro-Hungarian differential and integral geometer.His students included Shiing-Shen Chern, Luis Santaló, and Emanuel Sperner....
; the full result was proven much later by using a technique known as Steiner symmetrization by which any centrally symmetric convex body can be replaced with a more sphere-like body without decreasing its Mahler volume.
The shapes with the minimum known Mahler volume are hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
s, cross polytopes, and their Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
s and affine transformations. The Mahler conjecture states that the Mahler volume of these shapes is the smallest of any n-dimensional symmetric convex body; it remains unsolved. As Terry Tao
Terence Tao
Terence Chi-Shen Tao FRS is an Australian mathematician working primarily on harmonic analysis, partial differential equations, combinatorics, analytic number theory and representation theory...
writes:
prove that the Mahler volume is bounded below by cn times the volume of a sphere for some absolute constant c > 0, matching the scaling behavior of the hypercube volume but with a smaller constant. A result of this type is known as an inverse Santaló inequality.