Mathematics as a language
Encyclopedia
The language of mathematics is the system used by mathematician
s to communicate mathematical
ideas among themselves. This language consists of a substrate of some natural language
(for example English
) using technical terms and grammatical conventions that are peculiar to mathematical discourse (see Mathematical jargon
), supplemented by a highly specialized symbolic notation for mathematical formulas.
Like natural languages in general, discourse using the language of mathematics can employ a scala of register
s. Research articles in academic journals use a more formal tone than oral exchanges over a scribbled-upon napkin in the university cafeteria.
:
These definitions describe language in terms of the following components:
Each of these components is also found in the language of mathematics.
has assimilated symbols
from many different alphabet
s and typefaces
. It also includes symbols that are specific to mathematics, such as
Mathematical notation is central to the power of modern mathematics. Though the algebra
of Al-Khwārizmī did not use such symbols, it solved equations using many more rules than are used today with symbolic notation, and had great difficulty working with multiple variables (which using symbolic notation can simply be called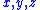
, etc.). Sometimes formulas cannot be understood without a written or spoken explanation, but often they are sufficient by themselves, and sometimes they are difficult to read aloud or information is lost in the translation to words, as when several parenthetical factors are involved or when a complex structure like a matrix
is manipulated.
Like any other profession, mathematics also has its own brand of technical terminology
. In some cases, a word in general usage has a different and specific meaning within mathematics—examples are group
, ring
, field
, category
, term
, and factor. For more examples, see :Category:Mathematical terminology.
In other cases, specialist terms have been created which do not exist outside of mathematics—examples are tensor
, fractal
, functor
. Mathematical statements have their own moderately complex taxonomy, being divided into axiom
s, conjecture
s, theorem
s, lemma
s and corollaries
. And there are stock phrases in mathematics, used with specific meanings, such as "if and only if
", "necessary and sufficient" and "without loss of generality
". Such phrases are known as mathematical jargon
.
When mathematicians communicate with each other informally, they use phrases that help to convey ideas. Examples of some of the more idiomatic phrases are "kill this term", "vanish this interval" and "grow this variable".
The vocabulary of mathematics also has visual elements. Diagrams are used informally on blackboards, as well as more formally in published work. When used appropriately, diagrams display schematic information more easily. Diagrams also help visually and aid intuitive calculations. Sometimes, as in a visual proof, a diagram even serves as complete justification for a proposition. A system of diagram conventions may evolve into a mathematical notation – for example, the Penrose graphical notation
for tensor products.
used for mathematical discourse is essentially the grammar of the natural language used as substrate, but with several mathematics-specific peculiarities.
Most notably, the mathematical notation used for formulas has its own grammar, not dependent on a specific natural language, but shared internationally by mathematicians regardless of their mother tongues. This includes the conventions that the formulas are written predominantly left to right
, also when the writing system of the substrate language is right-to-left, and that the Latin alphabet
is commonly used for simple variable
s and parameter
s. A formula such as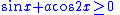
is understood by Chinese and Israeli mathematicians alike.
Such mathematical formulas can be a part of speech in a natural-language phrase, or even assume the role of a full-fludged sentence. For example, the formula above, an equation
, can be considered a sentence or sentential phrase in which the greater than or equal to symbol has the role of a verb
. In careful speech, this can be made clear by pronouncing "≥" as "is greater than or equal to", but in an informal context mathematicians may shorten this to "greater or equal" and yet handle this grammatically like a verb.
Mathematical formulas can be vocalized
(spoken aloud). The vocalization system for formulas has to be learned, and is dependent on the underlying natural language. For example, when using English, the expression "ƒ (x)" is conventionally pronounced "eff of eks", where the insertion of the preposition "of" is not suggested by the notation per se. The expression "
", on the other hand, is vocalized like "dee-why-dee-eks", with complete omission of the fraction bar, in other contexts often pronounced "over".
Characteristic for mathematical discourse – both formal and informal – is the use of the inclusive
first person
plural
"we" to mean: "the audience (or reader) together with the speaker (or author)".
, and international co-operation between professional mathematicians is commonplace.
Mathematics can communicate a range of meanings that is as wide as (although different from) that of a natural language. As German
mathematician R.L.E. Schwarzenberger says:
out loud). However, these definitions would also disqualify sign language
s, which are now recognized as languages in their own right, independent of spoken language.
Other linguists believe no valid comparison can be made between mathematics and language, because they are simply too different:
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s to communicate mathematical
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
ideas among themselves. This language consists of a substrate of some natural language
Natural language
In the philosophy of language, a natural language is any language which arises in an unpremeditated fashion as the result of the innate facility for language possessed by the human intellect. A natural language is typically used for communication, and may be spoken, signed, or written...
(for example English
English language
English is a West Germanic language that arose in the Anglo-Saxon kingdoms of England and spread into what was to become south-east Scotland under the influence of the Anglian medieval kingdom of Northumbria...
) using technical terms and grammatical conventions that are peculiar to mathematical discourse (see Mathematical jargon
Mathematical jargon
The language of mathematics has a vast vocabulary of specialist and technical terms. It also has a certain amount of jargon: commonly used phrases which are part of the culture of mathematics, rather than of the subject. Jargon often appears in lectures, and sometimes in print, as informal...
), supplemented by a highly specialized symbolic notation for mathematical formulas.
Like natural languages in general, discourse using the language of mathematics can employ a scala of register
Register (sociolinguistics)
In linguistics, a register is a variety of a language used for a particular purpose or in a particular social setting. For example, when speaking in a formal setting an English speaker may be more likely to adhere more closely to prescribed grammar, pronounce words ending in -ing with a velar nasal...
s. Research articles in academic journals use a more formal tone than oral exchanges over a scribbled-upon napkin in the university cafeteria.
What is a language?
Here are some definitions of languageLanguage
Language may refer either to the specifically human capacity for acquiring and using complex systems of communication, or to a specific instance of such a system of complex communication...
:
- a systematic means of communicating by the use of sounds or conventional symbols WordNet
- a system of words used in a particular discipline WordNet
- the code we all use to express ourselves and communicate to others Speech & Language Therapy Glossary of Terms
- a set (finite or infinite) of sentences, each finite in length and constructed out of a finite set of elements Noam ChomskyNoam ChomskyAvram Noam Chomsky is an American linguist, philosopher, cognitive scientist, and activist. He is an Institute Professor and Professor in the Department of Linguistics & Philosophy at MIT, where he has worked for over 50 years. Chomsky has been described as the "father of modern linguistics" and...
These definitions describe language in terms of the following components:
- A vocabularyVocabularyA person's vocabulary is the set of words within a language that are familiar to that person. A vocabulary usually develops with age, and serves as a useful and fundamental tool for communication and acquiring knowledge...
of symbols or words - A grammarGrammarIn linguistics, grammar is the set of structural rules that govern the composition of clauses, phrases, and words in any given natural language. The term refers also to the study of such rules, and this field includes morphology, syntax, and phonology, often complemented by phonetics, semantics,...
consisting of rules of how these symbols may be used - A communityCommunityThe term community has two distinct meanings:*a group of interacting people, possibly living in close proximity, and often refers to a group that shares some common values, and is attributed with social cohesion within a shared geographical location, generally in social units larger than a household...
of people who use and understand these symbols - A range of meaningsMeaning (semiotics)In semiotics, the meaning of a sign is its place in a sign relation, in other words, the set of roles that it occupies within a given sign relation. This statement holds whether sign is taken to mean a sign type or a sign token...
that can be communicated with these symbols
Each of these components is also found in the language of mathematics.
The vocabulary of mathematics
Mathematical notationMathematical notation
Mathematical notation is a system of symbolic representations of mathematical objects and ideas. Mathematical notations are used in mathematics, the physical sciences, engineering, and economics...
has assimilated symbols
Table of mathematical symbols
This is a listing of common symbols found within all branches of mathematics. Each symbol is listed in both HTML, which depends on appropriate fonts being installed, and in , as an image.-Symbols:-Variations:...
from many different alphabet
Alphabet
An alphabet is a standard set of letters—basic written symbols or graphemes—each of which represents a phoneme in a spoken language, either as it exists now or as it was in the past. There are other systems, such as logographies, in which each character represents a word, morpheme, or semantic...
s and typefaces
Typeface
In typography, a typeface is the artistic representation or interpretation of characters; it is the way the type looks. Each type is designed and there are thousands of different typefaces in existence, with new ones being developed constantly....
. It also includes symbols that are specific to mathematics, such as
Mathematical notation is central to the power of modern mathematics. Though the algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
of Al-Khwārizmī did not use such symbols, it solved equations using many more rules than are used today with symbolic notation, and had great difficulty working with multiple variables (which using symbolic notation can simply be called
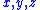, etc.). Sometimes formulas cannot be understood without a written or spoken explanation, but often they are sufficient by themselves, and sometimes they are difficult to read aloud or information is lost in the translation to words, as when several parenthetical factors are involved or when a complex structure like a matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
is manipulated.
Like any other profession, mathematics also has its own brand of technical terminology
Technical terminology
Technical terminology is the specialized vocabulary of any field, not just technical fields. The same is true of the synonyms technical terms, terms of art, shop talk and words of art, which do not necessarily refer to technology or art...
. In some cases, a word in general usage has a different and specific meaning within mathematics—examples are group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, term
Term (mathematics)
A term is a mathematical expression which may form a separable part of an equation, a series, or another expression.-Definition:In elementary mathematics, a term is either a single number or variable, or the product of several numbers or variables separated from another term by a + or - sign in an...
, and factor. For more examples, see :Category:Mathematical terminology.
In other cases, specialist terms have been created which do not exist outside of mathematics—examples are tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
, fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
, functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
. Mathematical statements have their own moderately complex taxonomy, being divided into axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s, conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
s, theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
s, lemma
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
s and corollaries
Corollary
A corollary is a statement that follows readily from a previous statement.In mathematics a corollary typically follows a theorem. The use of the term corollary, rather than proposition or theorem, is intrinsically subjective...
. And there are stock phrases in mathematics, used with specific meanings, such as "if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
", "necessary and sufficient" and "without loss of generality
Without loss of generality
Without loss of generality is a frequently used expression in mathematics...
". Such phrases are known as mathematical jargon
Mathematical jargon
The language of mathematics has a vast vocabulary of specialist and technical terms. It also has a certain amount of jargon: commonly used phrases which are part of the culture of mathematics, rather than of the subject. Jargon often appears in lectures, and sometimes in print, as informal...
.
When mathematicians communicate with each other informally, they use phrases that help to convey ideas. Examples of some of the more idiomatic phrases are "kill this term", "vanish this interval" and "grow this variable".
The vocabulary of mathematics also has visual elements. Diagrams are used informally on blackboards, as well as more formally in published work. When used appropriately, diagrams display schematic information more easily. Diagrams also help visually and aid intuitive calculations. Sometimes, as in a visual proof, a diagram even serves as complete justification for a proposition. A system of diagram conventions may evolve into a mathematical notation – for example, the Penrose graphical notation
Penrose graphical notation
In mathematics and physics, Penrose graphical notation or tensor diagram notation is a visual depiction of multilinear functions or tensors proposed by Roger Penrose. A diagram in the notation consists of several shapes linked together by lines, much like tinker toys...
for tensor products.
The grammar of mathematics
The grammarGrammar
In linguistics, grammar is the set of structural rules that govern the composition of clauses, phrases, and words in any given natural language. The term refers also to the study of such rules, and this field includes morphology, syntax, and phonology, often complemented by phonetics, semantics,...
used for mathematical discourse is essentially the grammar of the natural language used as substrate, but with several mathematics-specific peculiarities.
Most notably, the mathematical notation used for formulas has its own grammar, not dependent on a specific natural language, but shared internationally by mathematicians regardless of their mother tongues. This includes the conventions that the formulas are written predominantly left to right
Left to Right
Left to Right is a short story by science fiction writer Isaac Asimov, featured in the short story collection Gold.-Plot synopsis:Robert L. Forward has created a doughnut that is spinning at such a speed that something will interchange...
, also when the writing system of the substrate language is right-to-left, and that the Latin alphabet
Latin alphabet
The Latin alphabet, also called the Roman alphabet, is the most recognized alphabet used in the world today. It evolved from a western variety of the Greek alphabet called the Cumaean alphabet, which was adopted and modified by the Etruscans who ruled early Rome...
is commonly used for simple variable
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
s and parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
s. A formula such as
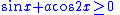
is understood by Chinese and Israeli mathematicians alike.
Such mathematical formulas can be a part of speech in a natural-language phrase, or even assume the role of a full-fludged sentence. For example, the formula above, an equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
, can be considered a sentence or sentential phrase in which the greater than or equal to symbol has the role of a verb
Verb
A verb, from the Latin verbum meaning word, is a word that in syntax conveys an action , or a state of being . In the usual description of English, the basic form, with or without the particle to, is the infinitive...
. In careful speech, this can be made clear by pronouncing "≥" as "is greater than or equal to", but in an informal context mathematicians may shorten this to "greater or equal" and yet handle this grammatically like a verb.
Mathematical formulas can be vocalized
Speech production
Speech production is the process by which spoken words are selected to be produced, have their phonetics formulated and then finally are articulated by the motor system in the vocal apparatus...
(spoken aloud). The vocalization system for formulas has to be learned, and is dependent on the underlying natural language. For example, when using English, the expression "ƒ (x)" is conventionally pronounced "eff of eks", where the insertion of the preposition "of" is not suggested by the notation per se. The expression "
", on the other hand, is vocalized like "dee-why-dee-eks", with complete omission of the fraction bar, in other contexts often pronounced "over".Characteristic for mathematical discourse – both formal and informal – is the use of the inclusive
Clusivity
In linguistics, clusivity is a distinction between inclusive and exclusive first-person pronouns and verbal morphology, also called inclusive "we" and exclusive "we"...
first person
Grammatical person
Grammatical person, in linguistics, is deictic reference to a participant in an event; such as the speaker, the addressee, or others. Grammatical person typically defines a language's set of personal pronouns...
plural
Plural
In linguistics, plurality or [a] plural is a concept of quantity representing a value of more-than-one. Typically applied to nouns, a plural word or marker is used to distinguish a value other than the default quantity of a noun, which is typically one...
"we" to mean: "the audience (or reader) together with the speaker (or author)".
The language community of mathematics
Mathematics is used by mathematicians, who form a global community composed of speakers of many languages. It is also used by students of mathematics. As mathematics is a part of primary education in almost all countries, almost all educated people have some exposure to pure mathematics. It is interesting to note that there are very few cultural dependencies or barriers in modern mathematics. There are international mathematics competitions, such as the International Mathematical OlympiadInternational Mathematical Olympiad
The International Mathematical Olympiad is an annual six-problem, 42-point mathematical olympiad for pre-collegiate students and is the oldest of the International Science Olympiads. The first IMO was held in Romania in 1959. It has since been held annually, except in 1980...
, and international co-operation between professional mathematicians is commonplace.
The meanings of mathematics
Mathematics is used to communicate information about a wide range of different subjects. Here are three broad categories:- Mathematics describes the real world: many areas of mathematics originated with attempts to describe and solve real world phenomena - from measuring farms (geometryGeometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
) to falling apples (calculusCalculusCalculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
) to gambling (probabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
). Mathematics is widely used in modern physicsMathematical physicsMathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
and engineeringEngineeringEngineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, and has been hugely successful in helping us to understand more about the universe around us from its largest scales (physical cosmologyPhysical cosmologyPhysical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...
) to its smallest (quantum mechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
). Indeed, the very success of mathematics in this respect has been a source of puzzlement for some philosophers (see The Unreasonable Effectiveness of Mathematics in the Natural SciencesThe Unreasonable Effectiveness of Mathematics in the Natural SciencesThe Unreasonable Effectiveness of Mathematics in the Natural Sciences is the title of an article published in 1960 by the physicist Eugene Wigner...
by Eugene Wigner).
- Mathematics describes abstract structures: on the other hand, there are areas of pure mathematics which deal with abstract structureAbstract structureAn abstract structure in mathematics is a formal object that is defined by a set of laws, properties, and relationships in a way that is logically if not always historically independent of the structure of contingent experiences, for example, those involving physical objects...
s, which have no known physical counterparts at all. However, it is difficult to give any categorical examples here, as even the most abstract structures can be co-opted as models in some branch of physics (see Calabi-Yau spaces and string theoryString theoryString theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
).
- Mathematics describes mathematics: mathematics can be used reflexively to describe itself—this is an area of mathematics called metamathematicsMetamathematicsMetamathematics is the study of mathematics itself using mathematical methods. This study produces metatheories, which are mathematical theories about other mathematical theories...
.
Mathematics can communicate a range of meanings that is as wide as (although different from) that of a natural language. As German
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
mathematician R.L.E. Schwarzenberger says:
- My own attitude, which I share with many of my colleagues, is simply that mathematics is a language. Like English, or Latin, or Chinese, there are certain concepts for which mathematics is particularly well suited: it would be as foolish to attempt to write a love poem in the language of mathematics as to prove the Fundamental Theorem of AlgebraFundamental theorem of algebraThe fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
using the English language. - Schwarzenberger (2000)
Alternative views
Some definitions of language, such as early versions of Charles Hockett's "design features" definition, emphasize the spoken nature of language. Mathematics would not qualify as a language under these definitions, as it is primarily a written form of communication (to see why, try reading Maxwell's equationsMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
out loud). However, these definitions would also disqualify sign language
Sign language
A sign language is a language which, instead of acoustically conveyed sound patterns, uses visually transmitted sign patterns to convey meaning—simultaneously combining hand shapes, orientation and movement of the hands, arms or body, and facial expressions to fluidly express a speaker's...
s, which are now recognized as languages in their own right, independent of spoken language.
Other linguists believe no valid comparison can be made between mathematics and language, because they are simply too different:
- Mathematics would appear to be both more and less than a language for while being limited in its linguistic capabilities it also seems to involve a form of thinking that has something in common with art and music. - Ford & Peat (1988)
External links
- What is Language
- Mathematics and the Language of Nature - essay by F. David Peat.
- Mathematical Words: Origins and Sources (John Aldrich, University of Southampton)
- Communicating in the Language of Mathematics by Dr. David Moursund