Montonen-Olive duality
Encyclopedia
In theoretical physics
, Montonen–Olive duality is the oldest known example of S-duality
or a strong-weak duality. It generalizes the electro-magnetic symmetry of Maxwell's equations
. It is named after Finnish
Claus Montonen and British
David Olive
.
g by 1/g. This also involves an interchange of the electrically charged particles and magnetic monopole
s. See also Seiberg duality
.
In fact, there exists a larger SL(2,Z)
symmetry where both g as well as theta-angle are transformed non-trivially.
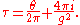
Since the theta-angle is periodic, there is a symmetry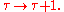
The quantum mechanical theory with gauge group G (but not the classical theory, except in the case when the G is abelian
) is also invariant under the symmetry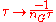
while the gauge group G is simultaneously replaced by its Langlands dual group LG and
is an integer depending on the choice of gauge group. In the case the theta-angle is 0, this reduces to the simple form of Montonen–Olive duality stated above.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, Montonen–Olive duality is the oldest known example of S-duality
S-duality
In theoretical physics, S-duality is an equivalence of two quantum field theories or string theories. An S-duality transformation maps states and vacua with coupling constant g in one theory to states and vacua with coupling constant 1/g in the dual theory...
or a strong-weak duality. It generalizes the electro-magnetic symmetry of Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
. It is named after Finnish
Finland
Finland , officially the Republic of Finland, is a Nordic country situated in the Fennoscandian region of Northern Europe. It is bordered by Sweden in the west, Norway in the north and Russia in the east, while Estonia lies to its south across the Gulf of Finland.Around 5.4 million people reside...
Claus Montonen and British
United Kingdom
The United Kingdom of Great Britain and Northern IrelandIn the United Kingdom and Dependencies, other languages have been officially recognised as legitimate autochthonous languages under the European Charter for Regional or Minority Languages...
David Olive
David Olive
David Olive CBE FLSW FRS, is a British theoretical physicist. Olive made fundamental contributions to the string theory and duality theory. He was Professor of physics at Imperial College, London...
.
Overview
In a four-dimensional Yang-Mills theory with N=4 supersymmetry, which is the case where the Montonen–Olive duality applies, one obtains a physically equivalent theory if one replaces the gauge coupling constantCoupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
g by 1/g. This also involves an interchange of the electrically charged particles and magnetic monopole
Magnetic monopole
A magnetic monopole is a hypothetical particle in particle physics that is a magnet with only one magnetic pole . In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring...
s. See also Seiberg duality
Seiberg duality
In quantum field theory, Seiberg duality, conjectured by Nathan Seiberg, is an S-duality relating two different supersymmetric QCDs. The two theories are not identical, but they agree at low energies. More precisely under a renormalization group flow they flow to the same IR fixed point, and so...
.
In fact, there exists a larger SL(2,Z)
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
symmetry where both g as well as theta-angle are transformed non-trivially.
Mathematical formalism
The gauge coupling and theta-angle can be combined together to form one complex coupling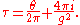Since the theta-angle is periodic, there is a symmetry
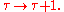
The quantum mechanical theory with gauge group G (but not the classical theory, except in the case when the G is abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
) is also invariant under the symmetry
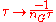
while the gauge group G is simultaneously replaced by its Langlands dual group LG and
is an integer depending on the choice of gauge group. In the case the theta-angle is 0, this reduces to the simple form of Montonen–Olive duality stated above.