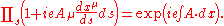Magnetic monopole
Encyclopedia
A magnetic monopole is a hypothetical particle
in particle physics
that is a magnet
with only one magnetic pole (a north pole
without a south pole
or vice-versa). In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring
theories, which predict their existence. Magnetism in bar magnets and electromagnet
s does not arise from magnetic monopoles, and in fact there is no conclusive experimental evidence that magnetic monopoles exist at all in the universe.
Many early scientists attributed the magnetism of lodestone
s to two different "magnetic fluids" ("effluvia"), a north-pole fluid at one end and a south-pole fluid at the other, which attracted and repelled each other in analogy to positive and negative electric charge
. However, an improved understanding of electromagnetism
in the nineteenth century showed that the magnetism of lodestones was caused by something else, not magnetic monopole fluids. It was concluded that magnetic monopoles did not exist: One of Maxwell's equations
, now called Gauss's law for magnetism, is the mathematical statement that there are no magnetic monopoles. Nevertheless, it was pointed out by Pierre Curie
in 1894 that magnetic monopoles could conceivably exist, despite not having been seen so far.
The quantum
theory of magnetic charge started with a paper by the physicist
Paul A.M. Dirac in 1931. In this paper, Dirac showed that if any magnetic monopoles exist in the universe, then all electric charge in the universe must be quantized. The electric charge is, in fact, quantized, which suggests (but does not necessarily prove) that monopoles exist.
Since Dirac's paper, several systematic monopole searches have been performed. Experiments in 1975 and 1982 produced candidate events that were initially interpreted as monopoles, but are now regarded as inconclusive. Therefore, it remains an open question whether or not monopoles exist.
Further advances in theoretical particle physics
, particularly developments in grand unified theories and quantum gravity
, have led to more compelling arguments that monopoles do exist. Joseph Polchinski
, a prominent string-theorist, described the existence of monopoles as "one of the safest bets that one can make about physics not yet seen". These theories are not necessarily inconsistent with the experimental evidence. In some theoretical model
s, magnetic monopoles are unlikely to be observed, because they are too massive to be created in particle accelerator
s, and also too rare in the Universe to enter a particle detector
with much probability.
Some condensed matter systems
propose a structure superficially similar to a magnetic monopole, known as a flux tube
. The ends of a flux tube form a magnetic dipole
, but since they move independently, they can be treated for many purposes as independent magnetic monopole quasiparticle
s. Since 2009, numerous news reports from the popular media have incorrectly described these systems as the long-awaited discovery of the magnetic monopoles, but the two phenomena are only superficially related to one another. These condensed-matter systems continue to be an area of active research. (See "Monopoles" in condensed-matter systems below.)
s exert force
s on one another, similar to the force associated with electric charge
s. Like poles will repel each other, and unlike poles will attract. When any magnet (an object conventionally described as having magnetic north and south poles) is cut in half across the axis joining those "poles", the resulting pieces are two normal (albeit smaller) magnets. Each has its own north pole and south pole.
Even atom
s and subatomic particle
s have tiny magnetic fields. In the Bohr model
of an atom, electrons orbit the nucleus. Their constant motion gives rise to a magnetic field
. Permanent magnets have measurable magnetic fields because the atoms and molecules in them are arranged in such a way that their individual magnetic fields align, combining to form large aggregate fields. In this model, the lack of a single pole makes intuitive sense: cutting a bar magnet in half does nothing to the arrangement of the molecules within. The end result is two bar magnetics whose atoms have the same orientation as before, and therefore generate a magnetic field with the same orientation as the original larger magnet.
of electromagnetism
relate the electric and magnetic fields to each other and to the motions of electric charges. The standard equations provide for electric charges, but they posit no magnetic charges. Except for this difference, the equations are symmetric under the interchange of the electric and magnetic fields. In fact, symmetric Maxwell's equations can be written when all charges (and hence electric current
s) are zero, and this is how the electromagnetic wave equation
is derived.
Fully symmetric Maxwell's equations can also be written if one allows for the possibility of "magnetic charges" analogous to electric charges. With the inclusion of a variable for the density of these magnetic charges, say ρm, there will also be a "magnetic current density" variable in the equations, jm.
If magnetic charges do not exist - or if they do exist but are not present in a region of space - then the new terms in Maxwell's equations are all zero, and the extended equations reduce to the conventional equations of electromagnetism such as ∇⋅B = 0 (where ∇ is divergence
and B is the magnetic B field
).
For a long time, the open question has been "Why does the magnetic charge always seem to be zero?"
units:
The equally-important Lorentz force equation
becomes

In these equations ρm is the magnetic charge density, jm is the magnetic current density, and qm is the magnetic charge of a test particle, all defined analogously to the related quantities of electric charge and current; v is the particle's velocity and c is the speed of light
.
units, there are two conflicting conventions in use for magnetic charge. In one, magnetic charge has units of webers
, while in the other, magnetic charge has units of ampere
-meters. Maxwell's equations then take the following forms:
In these equations ρm is the magnetic charge density, jm is the magnetic current density, and qm is the magnetic charge of a test particle, all defined analogously to the related quantities of electric charge and current.
was Paul Dirac
's work on developing a relativistic
quantum electromagnetism. Before his formulation, the presence of electric charge was simply "inserted" into the equations of quantum mechanics (QM), but in 1931 Dirac showed that a discrete charge naturally "falls out" of QM. That is to say, we can maintain the form of Maxwell's equations
and still have magnetic charges.
Consider a system consisting of a single stationary electric monopole (an electron, say) and a single stationary magnetic monopole. Classically, the electromagnetic field surrounding them has a momentum density given by the Poynting vector
, and it also has a total angular momentum
, which is proportional to the product qeqm, and independent of the distance between them.
Quantum mechanics dictates, however, that angular momentum is quantized in units of ħ, so therefore. the product qeqm must also be quantized. This means that if even a single magnetic monopole existed in the universe, and the form of Maxwell's equations
is valid, all electric charges would then be quantized
.
What are the units in which magnetic charge would be quantized? Although it would be possible simply to integrate over all space to find the total angular momentum in the above example, Dirac took a different approach. This led him to new ideas. He considered a point-like magnetic charge whose magnetic field behaves as qm / r 2 and is directed in the radial direction. Because the divergence of B is equal to zero almost everywhere, except for the locus of the magnetic monopole at r = 0, one can locally define the vector potential
such that the curl of the vector potential A equals the magnetic field B.
However, the vector potential cannot be defined globally precisely because the divergence of the magnetic field is proportional to the Dirac delta function
at the origin. We must define one set of functions for the vector potential on the northern hemisphere, and another set of functions for the southern hemispheres. These two vector potentials are matched at the equator, and they differ by a gauge transformation. The wave function of an electrically-charged particle (a "probe charge") that orbits the equator generally changes by a phase, much like in the Aharonov–Bohm effect. This phase is proportional to the electric charge qe of the probe, as well as to the magnetic charge qm of the source. Dirac was originally considering an electron
whose wave function is described by the Dirac equation
.
Because the electron returns to the same point after the full trip around the equator, the phase exp(iφ) of its wave function must be unchanged, which implies that the phase φ added to the wave function must be a multiple of 2π:
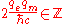 (cgs
(cgs
units)
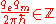 (SI units, weber
(SI units, weber
convention)
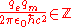 (SI
(SI
units, ampere
·meter convention)
where
This is known as the Dirac quantization condition. The hypothetical existence of a magnetic monopole would imply that the electric charge must be quantized in certain units; also, the existence of the electric charges implies that the magnetic charges of the hypothetical magnetic monopoles, if they exist, must be quantized in units inversely proportional to the elementary electric charge.
At the time it was not clear if such a thing existed, or even had to. After all, another theory could come along that would explain charge quantization without need for the monopole. The concept remained something of a curiosity. However, in the time since the publication of this seminal work, no other widely accepted explanation of charge quantization has appeared. (The concept of local gauge invariance—see gauge theory
below—provides a natural explanation of charge quantization, without invoking the need for magnetic monopoles; but only if the U(1) gauge group is compact, in which case we will have magnetic monopoles anyway.)
If we maximally extend the definition of the vector potential for the southern hemisphere, it will be defined everywhere except for a semi-infinite
line stretched from the origin in the direction towards the northern pole. This semi-infinite line is called the Dirac string
and its effect on the wave function is analogous to the effect of the solenoid
in the Aharonov–Bohm effect. The quantization condition comes from the requirement that the phases around the Dirac string are trivial, which means that the Dirac string must be unphysical. The Dirac string is merely an artifact of the coordinate chart used and should not be taken seriously.
The Dirac monopole is a singular solution of Maxwell's equation (because it requires removing the worldline from spacetime); in more complicated theories, it is superseded by a smooth solution such as the 't Hooft–Polyakov monopole.
In electrodynamics, the group is U(1), unit complex numbers under multiplication. For infinitesimal paths, the group element is 1+iAμdxμ which implies that for finite paths parametrized by s, the group element is:
The map from paths to group elements is called the Wilson loop
or the holonomy
, and for a U(1) gauge group it is the phase factor which the wavefunction of a charged particle acquires as it traverses the path. For a loop:
So that the phase a charged particle gets when going in a loop is the magnetic flux
through the loop. When a small solenoid
has a magnetic flux, there are interference fringes for charged particles which go around the solenoid, or around different sides of the solenoid, which reveal its presence.
But if all particle charges are integer multiples of e, solenoids with a flux of 2π/e have no interference fringes, because the phase factor for any charged particle is e2πi = 1. Such a solenoid, if thin enough, is quantum-mechanically invisible. If such a solenoid were to carry a flux of 2π/e, when the flux leaked out from one of its ends it would be indistinguishable from a monopole.
Dirac's monopole solution in fact describes an infinitesimal line solenoid ending at a point, and the location of the solenoid is the singular part of the solution, the Dirac string. Dirac strings link monopoles and antimonopoles of opposite magnetic charge, although in Dirac's version, the string just goes off to infinity. The string is unobservable, so you can put it anywhere, and by using two coordinate patches, the field in each patch can be made nonsingular by sliding the string to where it cannot be seen.
. Any U(1) which comes from a Grand Unified Theory is compact - because only compact higher gauge groups make sense. The size of the gauge group is a measure of the inverse coupling constant, so that in the limit of a large-volume gauge group, the interaction of any fixed representation goes to zero.
The case of the U(1) gauge group is a special case because all its irreducible representations are of the same size — the charge is bigger by an integer amount, but the field is still just a complex number — so that in U(1) gauge field theory it is possible to take the decompactified limit with no contradiction. The quantum of charge becomes small, but each charged particle has a huge number of charge quanta so its charge stays finite. In a non-compact U(1) gauge group theory, the charges of particles are generically not integer multiples of a single unit. Since charge quantization is an experimental certainty, it is clear that the U(1) gauge group of electromagnetism is compact.
GUTs lead to compact U(1) gauge groups, so they explain charge quantization in a way that seems to be logically independent from magnetic monopoles. However, the explanation is essentially the same, because in any GUT which breaks down into a U(1) gauge group at long distances, there are magnetic monopoles.
The argument is topological:
Hence, the Dirac monopole is a topological defect
in a compact U(1) gauge theory. When there is no GUT, the defect is a singularity — the core shrinks to a point. But when there is some sort of short-distance regulator on space time, the monopoles have a finite mass. Monopoles occur in lattice U(1)
, and there the core size is the lattice size. In general, they are expected to occur whenever there is a short-distance regulator.
, the lightest charged particles cannot be too heavy. The lightest monopole should have a mass less than or comparable to its charge in natural units
.
So in a consistent holographic theory, of which string theory
is the only known example, there are always finite-mass monopoles. For ordinary electromagnetism, the mass bound is not very useful because it is about same size as the Planck mass.
over a principal G-bundle
over spacetime. G is the gauge group, and it acts on each fiber of the bundle separately.
A connection on a G bundle tells you how to glue F's together at nearby points of M. It starts with a continuous symmetry group G which acts on F, and then it associates a group element with each infinitesimal path. Group multiplication along any path tells you how to move from one point on the bundle to another, by acting the G element of a path on the fiber F.
In mathematics, the definition of bundle is designed to emphasize topology, so the notion of connection is added on as an afterthought. In physics, the connection is the fundamental physical object. One of the fundamental observations in the theory of characteristic class
es in algebraic topology
is that many homotopical structures of nontrivial principal bundles may be expressed as an integral of some polynomial over any connection over it. Note that any connection over a trivial bundle can never give us a nontrivial principal bundle.
If space time has no topology, if it is R4 the space of all possible connections of the G-bundle is connected
. But consider what happens when we remove a timelike worldline from spacetime. The resulting spacetime is homotopically equivalent
to the topological sphere S2.
A principal G-bundle over S2 is defined by covering S2 by two charts, each homeomorphic to the open 2-ball such that their intersection is homeomorphic to the strip S1×I. 2-balls are homotopically trivial and the strip is homotopically equivalent to the circle S1. So a topological classification of the possible connections is reduced to classifying the transition functions. The transition function maps the strip to G, and the different ways of mapping a strip into G are given by the first homotopy group
of G.
So in the G-bundle formulation, a gauge theory admits Dirac monopoles provided G is not simply connected, whenever there are paths that go around the group that cannot be deformed to nothing. U(1), which has quantized charges, is not simply connected and can have Dirac monopoles while R, its universal covering group
, is simply connected, doesn't have quantized charges and does not admit Dirac monopoles. The mathematical definition is equivalent to the physics definition provided that, following Dirac, gauge fields are allowed which are defined only patch-wise and the gauge field on different patches are glued after a gauge transformation.
The total magnetic flux is none other than the first Chern number of the principal bundle, and depends only upon the choice of the principal bundle, and not the specific connection over it. In other words, it's a topological invariant.
This argument for monopoles is a restatement of the lasso argument for a pure U(1) theory. It generalizes to d + 1 dimensions with d ≥ 2 in several ways. One way is to extend everything into the extra dimensions, so that U(1) monopoles become sheets of dimension d-3. Another way is to examine the type of topological singularity at a point with the homotopy group πd−2(G).
During the early 1970s, the successes of quantum field theory
and gauge theory
in the development of electroweak theory and the mathematics of the strong nuclear force led many theorists to move on to attempt to combine them in a single theory known as a Grand Unified Theory (GUT). Several GUTs were proposed, most of which had the curious feature of implying the presence of a real magnetic monopole particle. More accurately, GUTs predicted a range of particles known as dyon
s, of which the most basic state was a monopole. The charge on magnetic monopoles predicted by GUTs is either 1 or 2 gD, depending on the theory.
The majority of particles appearing in any quantum field theory are unstable, and they decay into other particles in a variety of reactions that must satisfy various conservation law
s. Stable particles are stable because there are no lighter particles into which they can decay and still satisfy the conservation laws. For instance, the electron has a lepton number
of one and an electric charge of one, and there are no lighter particles that conserve these values. On the other hand, the muon
, essentially a heavy electron, can decay into the electron plus two quanta of energy, and hence it is not stable.
The dyons in these GUTs are also stable, but for an entirely different reason. The dyons are expected to exist as a side effect of the "freezing out" of the conditions of the early universe, or a symmetry breaking
. In this scenario, the dyons arise due to the configuration of the vacuum
in a particular area of the universe, according to the original Dirac theory. They remain stable not because of a conservation condition, but because there is no simpler topological
state into which they can decay.
The length scale over which this special vacuum configuration exists is called the correlation length of the system. A correlation length cannot be larger than causality
would allow, therefore the correlation length for making magnetic monopoles must be at least as big as the horizon size determined by the metric
of the expanding universe
. According to that logic, there should be at least one magnetic monopole per horizon volume as it was when the symmetry breaking took place. Other arguments based on the critical density of the universe indicate that monopoles should be fairly common; the apparent problem of the observed scarcity of monopoles is resolved by cosmic inflation
in the early universe, which greatly reduces the expected abundance of magnetic monopoles. For these reasons, monopoles became a major interest in the 1970s and 80s, along with the other "approachable" predictions of GUTs such as proton decay
.
Many of the other particles predicted by these GUTs were beyond the abilities of current experiments to detect. For instance, a wide class of particles known as the X and Y bosons
are predicted to mediate the coupling of the electroweak and strong forces, but these particles are extremely heavy and well beyond the capabilities of any reasonable particle accelerator
to create.
. Given the predicted density, loops small enough to fit on a lab bench would expect to see about one monopole event per year. Although there have been tantalizing events recorded, in particular the event recorded by Blas Cabrera
on the night of February 14, 1982 (thus, sometimes referred to as the "Valentine's Day Monopole"), there has never been reproducible evidence for the existence of magnetic monopoles. The lack of such events places a limit on the number of monopoles of about one monopole per 1029 nucleon
s.
Another experiment in 1975 resulted in the announcement of the detection of a moving magnetic monopole in cosmic ray
s by the team led by P. Buford Price
. Price later retracted his claim, and a possible alternative explanation was offered by Alvarez. In his paper it was demonstrated that the path of the cosmic ray event that was claimed to have been be due to a magnetic monopole could be reproduced by the path followed by a platinum
nucleus decaying first to osmium
, and then to tantalum
.
Other experiments rely on the strong coupling of monopoles with photon
s, as is the case for any electrically-charged particle as well. In experiments involving photon exchange in particle accelerators, monopoles should be produced in reasonable numbers, and detected due to their effect on the scattering of the photons. The probability of a particle being created in such experiments is related to their mass — with heavier particles being less likely to be created — so by examining the results of such experiments, limits on the mass of a magnetic monopole can be calculated. The most recent such experiments suggest that monopoles with masses below do not exist, while upper limits on their mass due to the very existence of the universe - which would have collapsed by now if they were too heavy - are about 1017 .
The MoEDAL experiment
, installed at the Large Hadron Collider
, is currently searching for magnetic monopoles and large supersymmetric particles using layers of special plastic sheets attached to the walls around LHCb
's VELO detector. The particles it is looking for will damage the sheets along their path, with various identifying features.
has never been conclusively observed, there are a number of phenomena in condensed-matter physics where a material, due to the collective behavior of its electrons and ions, can show emergent phenomena that resemble magnetic monopoles in some respect. These should not be confused with actual monopole particles: since all known particles have zero magnetic charge (including the proton
s, neutron
s, and electron
s that make up the whole periodic table
), it is fundamentally impossible to find a true magnetic monopole in ordinary matter made from atoms; only quasiparticle
s are possible. In particular, the law ∇⋅B=0 is true everywhere in these systems, which it would not be in the presence of a true magnetic monopole particle. The Dirac string
model describes such a system in the theoretical limit of infinitely thin connecting fluxtubes.
One example of the work on magnetic monopole quasiparticles is a paper published in the journal Science
in September 2009, in which researchers Jonathan Morris and Alan Tennant from the Helmholtz-Zentrum Berlin für Materialien und Energie
(HZB) along with Santiago Grigera from Instituto de Física de Líquidos y Sistemas Biológicos (IFLYSIB, CONICET) and other colleagues from Dresden University of Technology
, University of St. Andrews and Oxford University described the observation of quasiparticle
s resembling magnetic monopoles. A single crystal of dysprosium titanate
in a highly frustrated pyrochlore lattice
(F d -3 m) was cooled to a temperature between 0.6 kelvin
and 2.0 kelvin. Using observations of neutron scattering
, the magnetic moments were shown to align in the spin ice
into interwoven tubelike bundles resembling Dirac string
s. At the defect
formed by the end of each tube, the magnetic field looks like that of a monopole. Using an applied magnetic field to break the symmetry of the system, the researchers were able to control the density and orientation of these strings. A contribution to the heat capacity
of the system from an effective gas of these quasiparticles was also described.
Another example of the work on magnetic monopole quasiparticles is a paper in the February 11, 2011 issue of Nature Physics
which describes creation and measurement of long-lived magnetic monopole quasiparticle currents in spin ice. By applying a magnetic-field pulse to a dysprosium titanate (Dy2Ti2O7)
spin-ice crystal at 0.36 K, the authors created a relaxing magnetic current that lasted for several minutes. They measured the current by means of the electromotive force it induced in a solenoid coupled to a sensitive amplifier, and quantitatively described it using a chemical kinetic model of point-like charges obeying the Onsager–Wien mechanism of carrier dissociation and recombination. They thus derived the microscopic parameters of monopole motion in spin ice and identified the distinct roles of free and bound magnetic charges.
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
in particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
that is a magnet
Magnet
A magnet is a material or object that produces a magnetic field. This magnetic field is invisible but is responsible for the most notable property of a magnet: a force that pulls on other ferromagnetic materials, such as iron, and attracts or repels other magnets.A permanent magnet is an object...
with only one magnetic pole (a north pole
Magnet
A magnet is a material or object that produces a magnetic field. This magnetic field is invisible but is responsible for the most notable property of a magnet: a force that pulls on other ferromagnetic materials, such as iron, and attracts or repels other magnets.A permanent magnet is an object...
without a south pole
Magnet
A magnet is a material or object that produces a magnetic field. This magnetic field is invisible but is responsible for the most notable property of a magnet: a force that pulls on other ferromagnetic materials, such as iron, and attracts or repels other magnets.A permanent magnet is an object...
or vice-versa). In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring
Superstring theory
Superstring theory is an attempt to explain all of the particles and fundamental forces of nature in one theory by modelling them as vibrations of tiny supersymmetric strings...
theories, which predict their existence. Magnetism in bar magnets and electromagnet
Electromagnet
An electromagnet is a type of magnet in which the magnetic field is produced by the flow of electric current. The magnetic field disappears when the current is turned off...
s does not arise from magnetic monopoles, and in fact there is no conclusive experimental evidence that magnetic monopoles exist at all in the universe.
Many early scientists attributed the magnetism of lodestone
Lodestone
A lodestone or loadstone is a naturally magnetized piece of the mineral magnetite. They are naturally occurring magnets, that attract pieces of iron. Ancient people first discovered the property of magnetism in lodestone...
s to two different "magnetic fluids" ("effluvia"), a north-pole fluid at one end and a south-pole fluid at the other, which attracted and repelled each other in analogy to positive and negative electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
. However, an improved understanding of electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
in the nineteenth century showed that the magnetism of lodestones was caused by something else, not magnetic monopole fluids. It was concluded that magnetic monopoles did not exist: One of Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, now called Gauss's law for magnetism, is the mathematical statement that there are no magnetic monopoles. Nevertheless, it was pointed out by Pierre Curie
Pierre Curie
Pierre Curie was a French physicist, a pioneer in crystallography, magnetism, piezoelectricity and radioactivity, and Nobel laureate. He was the son of Dr. Eugène Curie and Sophie-Claire Depouilly Curie ...
in 1894 that magnetic monopoles could conceivably exist, despite not having been seen so far.
The quantum
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
theory of magnetic charge started with a paper by the physicist
Physicist
A physicist is a scientist who studies or practices physics. Physicists study a wide range of physical phenomena in many branches of physics spanning all length scales: from sub-atomic particles of which all ordinary matter is made to the behavior of the material Universe as a whole...
Paul A.M. Dirac in 1931. In this paper, Dirac showed that if any magnetic monopoles exist in the universe, then all electric charge in the universe must be quantized. The electric charge is, in fact, quantized, which suggests (but does not necessarily prove) that monopoles exist.
Since Dirac's paper, several systematic monopole searches have been performed. Experiments in 1975 and 1982 produced candidate events that were initially interpreted as monopoles, but are now regarded as inconclusive. Therefore, it remains an open question whether or not monopoles exist.
Further advances in theoretical particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
, particularly developments in grand unified theories and quantum gravity
Quantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
, have led to more compelling arguments that monopoles do exist. Joseph Polchinski
Joseph Polchinski
Joseph Polchinski is a physicist working on string theory. He graduated from Canyon del Oro High School in Tucson, Arizona in 1971, obtained his B.S. degree from Caltech in 1975, and his Ph.D. from the University of California, Berkeley in 1980 under the supervision of Stanley Mandelstam...
, a prominent string-theorist, described the existence of monopoles as "one of the safest bets that one can make about physics not yet seen". These theories are not necessarily inconsistent with the experimental evidence. In some theoretical model
Scientific modelling
Scientific modelling is the process of generating abstract, conceptual, graphical and/or mathematical models. Science offers a growing collection of methods, techniques and theory about all kinds of specialized scientific modelling...
s, magnetic monopoles are unlikely to be observed, because they are too massive to be created in particle accelerator
Particle accelerator
A particle accelerator is a device that uses electromagnetic fields to propel charged particles to high speeds and to contain them in well-defined beams. An ordinary CRT television set is a simple form of accelerator. There are two basic types: electrostatic and oscillating field accelerators.In...
s, and also too rare in the Universe to enter a particle detector
Particle detector
In experimental and applied particle physics, nuclear physics, and nuclear engineering, a particle detector, also known as a radiation detector, is a device used to detect, track, and/or identify high-energy particles, such as those produced by nuclear decay, cosmic radiation, or reactions in a...
with much probability.
Some condensed matter systems
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
propose a structure superficially similar to a magnetic monopole, known as a flux tube
Flux tube
A flux tube is a generally tube-like region of space containing a magnetic field, such that the field at the side surfaces is parallel to those surfaces...
. The ends of a flux tube form a magnetic dipole
Magnetic dipole
A magnetic dipole is the limit of either a closed loop of electric current or a pair of poles as the dimensions of the source are reduced to zero while keeping the magnetic moment constant. It is a magnetic analogue of the electric dipole, but the analogy is not complete. In particular, a magnetic...
, but since they move independently, they can be treated for many purposes as independent magnetic monopole quasiparticle
Quasiparticle
In physics, quasiparticles are emergent phenomena that occur when a microscopically complicated system such as a solid behaves as if it contained different weakly interacting particles in free space...
s. Since 2009, numerous news reports from the popular media have incorrectly described these systems as the long-awaited discovery of the magnetic monopoles, but the two phenomena are only superficially related to one another. These condensed-matter systems continue to be an area of active research. (See "Monopoles" in condensed-matter systems below.)
Background
MagnetMagnet
A magnet is a material or object that produces a magnetic field. This magnetic field is invisible but is responsible for the most notable property of a magnet: a force that pulls on other ferromagnetic materials, such as iron, and attracts or repels other magnets.A permanent magnet is an object...
s exert force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s on one another, similar to the force associated with electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
s. Like poles will repel each other, and unlike poles will attract. When any magnet (an object conventionally described as having magnetic north and south poles) is cut in half across the axis joining those "poles", the resulting pieces are two normal (albeit smaller) magnets. Each has its own north pole and south pole.
Even atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s and subatomic particle
Subatomic particle
In physics or chemistry, subatomic particles are the smaller particles composing nucleons and atoms. There are two types of subatomic particles: elementary particles, which are not made of other particles, and composite particles...
s have tiny magnetic fields. In the Bohr model
Bohr model
In atomic physics, the Bohr model, introduced by Niels Bohr in 1913, depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus—similar in structure to the solar system, but with electrostatic forces providing attraction,...
of an atom, electrons orbit the nucleus. Their constant motion gives rise to a magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
. Permanent magnets have measurable magnetic fields because the atoms and molecules in them are arranged in such a way that their individual magnetic fields align, combining to form large aggregate fields. In this model, the lack of a single pole makes intuitive sense: cutting a bar magnet in half does nothing to the arrangement of the molecules within. The end result is two bar magnetics whose atoms have the same orientation as before, and therefore generate a magnetic field with the same orientation as the original larger magnet.
Maxwell's equations
Maxwell's equationsMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
of electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
relate the electric and magnetic fields to each other and to the motions of electric charges. The standard equations provide for electric charges, but they posit no magnetic charges. Except for this difference, the equations are symmetric under the interchange of the electric and magnetic fields. In fact, symmetric Maxwell's equations can be written when all charges (and hence electric current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
s) are zero, and this is how the electromagnetic wave equation
Electromagnetic wave equation
The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
is derived.
Fully symmetric Maxwell's equations can also be written if one allows for the possibility of "magnetic charges" analogous to electric charges. With the inclusion of a variable for the density of these magnetic charges, say ρm, there will also be a "magnetic current density" variable in the equations, jm.
If magnetic charges do not exist - or if they do exist but are not present in a region of space - then the new terms in Maxwell's equations are all zero, and the extended equations reduce to the conventional equations of electromagnetism such as ∇⋅B = 0 (where ∇ is divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
and B is the magnetic B field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
).
For a long time, the open question has been "Why does the magnetic charge always seem to be zero?"
In cgs units
The extended Maxwell's equations are as follows, in cgsGaussian units
Gaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
units:
| Name | Without magnetic monopoles | With magnetic monopoles | |
|---|---|---|---|
| Gauss's law Gauss's law In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:... : |
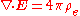 |
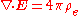 |
|
| Gauss's law for magnetism: |  |
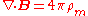 |
|
| Faraday's law of induction Faraday's law of induction Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators... : |
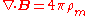 |
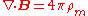 |
|
| Ampère's law Ampère's law In classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop... (with Maxwell's extension): |
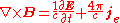 |
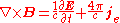 |
|
 and and 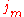 are defined above. For all other definitions and details, see Maxwell's equations are defined above. For all other definitions and details, see Maxwell's equationsMaxwell's equations Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations... article. |
|||
| Note: For the equations in nondimensionalized form, remove the factors of c. | |||
The equally-important Lorentz force equation
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
becomes

In these equations ρm is the magnetic charge density, jm is the magnetic current density, and qm is the magnetic charge of a test particle, all defined analogously to the related quantities of electric charge and current; v is the particle's velocity and c is the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
.
In SI units
In SISi
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units, there are two conflicting conventions in use for magnetic charge. In one, magnetic charge has units of webers
Weber (unit)
In physics, the weber is the SI unit of magnetic flux. A flux density of one Wb/m2 is one tesla.The weber is named for the German physicist Wilhelm Eduard Weber .- Definition :...
, while in the other, magnetic charge has units of ampere
Ampere
The ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics...
-meters. Maxwell's equations then take the following forms:
| Name | Without magnetic monopoles | Weber convention | Ampere·meter convention |
|---|---|---|---|
| Gauss's Law |  |
 |
 |
| Gauss's Law for magnetism |  |
 |
 |
| Faraday's Law of induction | 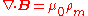 |
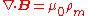 |
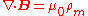 |
| Ampère's Law | 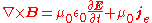 |
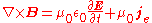 |
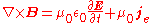 |
| Lorentz force equation |  |
  |
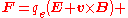 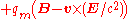 |
In these equations ρm is the magnetic charge density, jm is the magnetic current density, and qm is the magnetic charge of a test particle, all defined analogously to the related quantities of electric charge and current.
Dirac's quantization
One of the defining advances in quantum theoryQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
was Paul Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
's work on developing a relativistic
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
quantum electromagnetism. Before his formulation, the presence of electric charge was simply "inserted" into the equations of quantum mechanics (QM), but in 1931 Dirac showed that a discrete charge naturally "falls out" of QM. That is to say, we can maintain the form of Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
and still have magnetic charges.
Consider a system consisting of a single stationary electric monopole (an electron, say) and a single stationary magnetic monopole. Classically, the electromagnetic field surrounding them has a momentum density given by the Poynting vector
Poynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
, and it also has a total angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
, which is proportional to the product qeqm, and independent of the distance between them.
Quantum mechanics dictates, however, that angular momentum is quantized in units of ħ, so therefore. the product qeqm must also be quantized. This means that if even a single magnetic monopole existed in the universe, and the form of Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
is valid, all electric charges would then be quantized
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
.
What are the units in which magnetic charge would be quantized? Although it would be possible simply to integrate over all space to find the total angular momentum in the above example, Dirac took a different approach. This led him to new ideas. He considered a point-like magnetic charge whose magnetic field behaves as qm / r 2 and is directed in the radial direction. Because the divergence of B is equal to zero almost everywhere, except for the locus of the magnetic monopole at r = 0, one can locally define the vector potential
Vector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
such that the curl of the vector potential A equals the magnetic field B.
However, the vector potential cannot be defined globally precisely because the divergence of the magnetic field is proportional to the Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
at the origin. We must define one set of functions for the vector potential on the northern hemisphere, and another set of functions for the southern hemispheres. These two vector potentials are matched at the equator, and they differ by a gauge transformation. The wave function of an electrically-charged particle (a "probe charge") that orbits the equator generally changes by a phase, much like in the Aharonov–Bohm effect. This phase is proportional to the electric charge qe of the probe, as well as to the magnetic charge qm of the source. Dirac was originally considering an electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
whose wave function is described by the Dirac equation
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
.
Because the electron returns to the same point after the full trip around the equator, the phase exp(iφ) of its wave function must be unchanged, which implies that the phase φ added to the wave function must be a multiple of 2π:
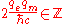 (cgs
(cgsGaussian units
Gaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
units)
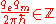 (SI units, weber
(SI units, weberWeber (unit)
In physics, the weber is the SI unit of magnetic flux. A flux density of one Wb/m2 is one tesla.The weber is named for the German physicist Wilhelm Eduard Weber .- Definition :...
convention)
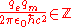 (SI
(SISi
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units, ampere
Ampere
The ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics...
·meter convention)
where
 is vacuum permittivity
is vacuum permittivity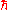 is reduced Planck's constant
is reduced Planck's constant is speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
is speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time... is the set of integersIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
is the set of integersIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
.
This is known as the Dirac quantization condition. The hypothetical existence of a magnetic monopole would imply that the electric charge must be quantized in certain units; also, the existence of the electric charges implies that the magnetic charges of the hypothetical magnetic monopoles, if they exist, must be quantized in units inversely proportional to the elementary electric charge.
At the time it was not clear if such a thing existed, or even had to. After all, another theory could come along that would explain charge quantization without need for the monopole. The concept remained something of a curiosity. However, in the time since the publication of this seminal work, no other widely accepted explanation of charge quantization has appeared. (The concept of local gauge invariance—see gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
below—provides a natural explanation of charge quantization, without invoking the need for magnetic monopoles; but only if the U(1) gauge group is compact, in which case we will have magnetic monopoles anyway.)
If we maximally extend the definition of the vector potential for the southern hemisphere, it will be defined everywhere except for a semi-infinite
Semi-infinite
The term semi-infinite has several related meanings in various branches of pure and applied mathematics. It typically describes objects which are infinite or unbounded in some but not all possible ways.-In ordered structures and Euclidean spaces:...
line stretched from the origin in the direction towards the northern pole. This semi-infinite line is called the Dirac string
Dirac string
In physics, a Dirac string is a fictitious one-dimensional curve in space, conceived of by the physicist Paul Dirac, stretching between two Dirac magnetic monopoles with opposite magnetic charges, or from one magnetic monopole out to infinity. The gauge potential cannot be defined on the Dirac...
and its effect on the wave function is analogous to the effect of the solenoid
Solenoid
A solenoid is a coil wound into a tightly packed helix. In physics, the term solenoid refers to a long, thin loop of wire, often wrapped around a metallic core, which produces a magnetic field when an electric current is passed through it. Solenoids are important because they can create...
in the Aharonov–Bohm effect. The quantization condition comes from the requirement that the phases around the Dirac string are trivial, which means that the Dirac string must be unphysical. The Dirac string is merely an artifact of the coordinate chart used and should not be taken seriously.
The Dirac monopole is a singular solution of Maxwell's equation (because it requires removing the worldline from spacetime); in more complicated theories, it is superseded by a smooth solution such as the 't Hooft–Polyakov monopole.
Dirac string
A gauge theory like electromagnetism is defined by a gauge field, which associates a group element to each path in space time. For infinitesimal paths, the group element is close to the identity, while for longer paths the group element is the successive product of the infinitesimal group elements along the way.In electrodynamics, the group is U(1), unit complex numbers under multiplication. For infinitesimal paths, the group element is 1+iAμdxμ which implies that for finite paths parametrized by s, the group element is:
The map from paths to group elements is called the Wilson loop
Wilson loop
In gauge theory, a Wilson loop is a gauge-invariant observable obtained from the holonomy of the gauge connection around a given loop...
or the holonomy
Holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
, and for a U(1) gauge group it is the phase factor which the wavefunction of a charged particle acquires as it traverses the path. For a loop:
So that the phase a charged particle gets when going in a loop is the magnetic flux
Magnetic flux
Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber...
through the loop. When a small solenoid
Solenoid
A solenoid is a coil wound into a tightly packed helix. In physics, the term solenoid refers to a long, thin loop of wire, often wrapped around a metallic core, which produces a magnetic field when an electric current is passed through it. Solenoids are important because they can create...
has a magnetic flux, there are interference fringes for charged particles which go around the solenoid, or around different sides of the solenoid, which reveal its presence.
But if all particle charges are integer multiples of e, solenoids with a flux of 2π/e have no interference fringes, because the phase factor for any charged particle is e2πi = 1. Such a solenoid, if thin enough, is quantum-mechanically invisible. If such a solenoid were to carry a flux of 2π/e, when the flux leaked out from one of its ends it would be indistinguishable from a monopole.
Dirac's monopole solution in fact describes an infinitesimal line solenoid ending at a point, and the location of the solenoid is the singular part of the solution, the Dirac string. Dirac strings link monopoles and antimonopoles of opposite magnetic charge, although in Dirac's version, the string just goes off to infinity. The string is unobservable, so you can put it anywhere, and by using two coordinate patches, the field in each patch can be made nonsingular by sliding the string to where it cannot be seen.
Grand unified theories
In a U(1) gauge group with quantized charge, the group is a circle of radius 2π/e. Such a U(1) gauge group is called compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
. Any U(1) which comes from a Grand Unified Theory is compact - because only compact higher gauge groups make sense. The size of the gauge group is a measure of the inverse coupling constant, so that in the limit of a large-volume gauge group, the interaction of any fixed representation goes to zero.
The case of the U(1) gauge group is a special case because all its irreducible representations are of the same size — the charge is bigger by an integer amount, but the field is still just a complex number — so that in U(1) gauge field theory it is possible to take the decompactified limit with no contradiction. The quantum of charge becomes small, but each charged particle has a huge number of charge quanta so its charge stays finite. In a non-compact U(1) gauge group theory, the charges of particles are generically not integer multiples of a single unit. Since charge quantization is an experimental certainty, it is clear that the U(1) gauge group of electromagnetism is compact.
GUTs lead to compact U(1) gauge groups, so they explain charge quantization in a way that seems to be logically independent from magnetic monopoles. However, the explanation is essentially the same, because in any GUT which breaks down into a U(1) gauge group at long distances, there are magnetic monopoles.
The argument is topological:
- The holonomy of a gauge field maps loops to elements of the gauge group. Infinitesimal loops are mapped to group elements infinitesimally close to the identity.
- If you imagine a big sphere in space, you can deform an infinitesimal loop which starts and ends at the north pole as follows: stretch out the loop over the western hemisphere until it becomes a great circle (which still starts and ends at the north pole) then let it shrink back to a little loop while going over the eastern hemisphere. This is called lassoing the spherePoincaré conjectureIn mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...
. - Lassoing is a sequence of loops, so the holonomy maps it to a sequence of group elements, a continuous path in the gauge group. Since the loop at the beginning of the lassoing is the same as the loop at the end, the path in the group is closed.
- If the group path associated to the lassoing procedure winds around the U(1), the sphere contains magnetic charge. During the lassoing, the holonomy changes by the amount of magnetic flux through the sphere.
- Since the holonomy at the beginning and at the end is the identity, the total magnetic flux is quantized. The magnetic charge is proportional to the number of windings N, the magnetic flux through the sphere is equal to 2πN/e. This is the Dirac quantization condition, and it is a topological condition which demands that the long distance U(1) gauge field configurations be consistent.
- When the U(1) gauge group comes from breaking a compact Lie group, the path which winds around the U(1) group enough times is topologically trivial in the big group. In a non-U(1) compact Lie group, the covering space is a Lie group with the same Lie algebra, but where all closed loops are contractible. Lie groups are homogenous, so that any cycle in the group can be moved around so that it starts at the identity, then its lift to the covering group ends at P, which is a lift of the identity. Going around the loop twice gets you to P2, three times to P3, all lifts of the identity. But there are only finitely many lifts of the identity, because the lifts can't accumulate. This number of times one has to traverse the loop to make it contractible is small, for example if the GUT group is SO(3), the covering group is SU(2), and going around any loop twice is enough.
- This means that there is a continuous gauge-field configuration in the GUT group allows the U(1) monopole configuration to unwind itself at short distances, at the cost of not staying in the U(1). In order to do this with as little energy as possible, you should leave only the U(1) gauge group in the neighborhood of one point, which is called the core of the monopole. Outside the core, the monopole has only magnetic field energy.
Hence, the Dirac monopole is a topological defect
Topological defect
In mathematics and physics, a topological soliton or a topological defect is a solution of a system of partial differential equations or of a quantum field theory homotopically distinct from the vacuum solution; it can be proven to exist because the boundary conditions entail the existence of...
in a compact U(1) gauge theory. When there is no GUT, the defect is a singularity — the core shrinks to a point. But when there is some sort of short-distance regulator on space time, the monopoles have a finite mass. Monopoles occur in lattice U(1)
Lattice gauge theory
In physics, lattice gauge theory is the study of gauge theories on a spacetime that has been discretized into a lattice. Gauge theories are important in particle physics, and include the prevailing theories of elementary particles: quantum electrodynamics, quantum chromodynamics and the Standard...
, and there the core size is the lattice size. In general, they are expected to occur whenever there is a short-distance regulator.
String theory
In our universe, quantum gravity provides the regulator. When gravity is included, the monopole singularity can be a black hole, and for large magnetic charge and mass, the black hole mass is equal to the black hole charge, so that the mass of the magnetic black hole is not infinite. If the black hole can decay completely by Hawking radiationHawking radiation
Hawking radiation is a thermal radiation with a black body spectrum predicted to be emitted by black holes due to quantum effects. It is named after the physicist Stephen Hawking, who provided a theoretical argument for its existence in 1974, and sometimes also after the physicist Jacob Bekenstein...
, the lightest charged particles cannot be too heavy. The lightest monopole should have a mass less than or comparable to its charge in natural units
Natural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
.
So in a consistent holographic theory, of which string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
is the only known example, there are always finite-mass monopoles. For ordinary electromagnetism, the mass bound is not very useful because it is about same size as the Planck mass.
Mathematical formulation
In mathematics, a gauge field is defined as a connectionConnection form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
over a principal G-bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
over spacetime. G is the gauge group, and it acts on each fiber of the bundle separately.
A connection on a G bundle tells you how to glue F's together at nearby points of M. It starts with a continuous symmetry group G which acts on F, and then it associates a group element with each infinitesimal path. Group multiplication along any path tells you how to move from one point on the bundle to another, by acting the G element of a path on the fiber F.
In mathematics, the definition of bundle is designed to emphasize topology, so the notion of connection is added on as an afterthought. In physics, the connection is the fundamental physical object. One of the fundamental observations in the theory of characteristic class
Characteristic class
In mathematics, a characteristic class is a way of associating to each principal bundle on a topological space X a cohomology class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses sections or not...
es in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
is that many homotopical structures of nontrivial principal bundles may be expressed as an integral of some polynomial over any connection over it. Note that any connection over a trivial bundle can never give us a nontrivial principal bundle.
If space time has no topology, if it is R4 the space of all possible connections of the G-bundle is connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
. But consider what happens when we remove a timelike worldline from spacetime. The resulting spacetime is homotopically equivalent
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
to the topological sphere S2.
A principal G-bundle over S2 is defined by covering S2 by two charts, each homeomorphic to the open 2-ball such that their intersection is homeomorphic to the strip S1×I. 2-balls are homotopically trivial and the strip is homotopically equivalent to the circle S1. So a topological classification of the possible connections is reduced to classifying the transition functions. The transition function maps the strip to G, and the different ways of mapping a strip into G are given by the first homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
of G.
So in the G-bundle formulation, a gauge theory admits Dirac monopoles provided G is not simply connected, whenever there are paths that go around the group that cannot be deformed to nothing. U(1), which has quantized charges, is not simply connected and can have Dirac monopoles while R, its universal covering group
Universal covering group
In mathematics, a covering group of a topological group H is a covering space G of H such that G is a topological group and the covering map p : G → H is a continuous group homomorphism. The map p is called the covering homomorphism...
, is simply connected, doesn't have quantized charges and does not admit Dirac monopoles. The mathematical definition is equivalent to the physics definition provided that, following Dirac, gauge fields are allowed which are defined only patch-wise and the gauge field on different patches are glued after a gauge transformation.
The total magnetic flux is none other than the first Chern number of the principal bundle, and depends only upon the choice of the principal bundle, and not the specific connection over it. In other words, it's a topological invariant.
This argument for monopoles is a restatement of the lasso argument for a pure U(1) theory. It generalizes to d + 1 dimensions with d ≥ 2 in several ways. One way is to extend everything into the extra dimensions, so that U(1) monopoles become sheets of dimension d-3. Another way is to examine the type of topological singularity at a point with the homotopy group πd−2(G).
Grand unified theories
In more recent years, a new class of theories has also suggested the existence of magnetic monopoles.During the early 1970s, the successes of quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
and gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
in the development of electroweak theory and the mathematics of the strong nuclear force led many theorists to move on to attempt to combine them in a single theory known as a Grand Unified Theory (GUT). Several GUTs were proposed, most of which had the curious feature of implying the presence of a real magnetic monopole particle. More accurately, GUTs predicted a range of particles known as dyon
Dyon
In physics, a dyon is a hypothetical particle in 4-dimensional theories with both electric and magnetic charges. A dyon with a zero electric charge is usually referred to as a magnetic monopole. Many grand unified theories predict the existence of both magnetic monopoles and dyons.Dyons were first...
s, of which the most basic state was a monopole. The charge on magnetic monopoles predicted by GUTs is either 1 or 2 gD, depending on the theory.
The majority of particles appearing in any quantum field theory are unstable, and they decay into other particles in a variety of reactions that must satisfy various conservation law
Conservation law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
s. Stable particles are stable because there are no lighter particles into which they can decay and still satisfy the conservation laws. For instance, the electron has a lepton number
Lepton number
In particle physics, the lepton number is the number of leptons minus the number of antileptons.In equation form,so all leptons have assigned a value of +1, antileptons −1, and non-leptonic particles 0...
of one and an electric charge of one, and there are no lighter particles that conserve these values. On the other hand, the muon
Muon
The muon |mu]] used to represent it) is an elementary particle similar to the electron, with a unitary negative electric charge and a spin of ½. Together with the electron, the tau, and the three neutrinos, it is classified as a lepton...
, essentially a heavy electron, can decay into the electron plus two quanta of energy, and hence it is not stable.
The dyons in these GUTs are also stable, but for an entirely different reason. The dyons are expected to exist as a side effect of the "freezing out" of the conditions of the early universe, or a symmetry breaking
Symmetry breaking
Symmetry breaking in physics describes a phenomenon where small fluctuations acting on a system which is crossing a critical point decide the system's fate, by determining which branch of a bifurcation is taken. To an outside observer unaware of the fluctuations , the choice will appear arbitrary...
. In this scenario, the dyons arise due to the configuration of the vacuum
Vacuum
In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
in a particular area of the universe, according to the original Dirac theory. They remain stable not because of a conservation condition, but because there is no simpler topological
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
state into which they can decay.
The length scale over which this special vacuum configuration exists is called the correlation length of the system. A correlation length cannot be larger than causality
Causality (physics)
Causality is the relationship between causes and effects. It is considered to be fundamental to all natural science, especially physics. Causality is also a topic studied from the perspectives of philosophy and statistics....
would allow, therefore the correlation length for making magnetic monopoles must be at least as big as the horizon size determined by the metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
of the expanding universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
. According to that logic, there should be at least one magnetic monopole per horizon volume as it was when the symmetry breaking took place. Other arguments based on the critical density of the universe indicate that monopoles should be fairly common; the apparent problem of the observed scarcity of monopoles is resolved by cosmic inflation
Cosmic inflation
In physical cosmology, cosmic inflation, cosmological inflation or just inflation is the theorized extremely rapid exponential expansion of the early universe by a factor of at least 1078 in volume, driven by a negative-pressure vacuum energy density. The inflationary epoch comprises the first part...
in the early universe, which greatly reduces the expected abundance of magnetic monopoles. For these reasons, monopoles became a major interest in the 1970s and 80s, along with the other "approachable" predictions of GUTs such as proton decay
Proton decay
In particle physics, proton decay is a hypothetical form of radioactive decay in which the proton decays into lighter subatomic particles, such as a neutral pion and a positron...
.
Many of the other particles predicted by these GUTs were beyond the abilities of current experiments to detect. For instance, a wide class of particles known as the X and Y bosons
X and Y bosons
In particle physics, the X and Y bosons are hypothetical elementary particles analogous to the W and Z bosons, but corresponding to a new type of force predicted by the Georgi–Glashow model, a grand unified theory.-Details:The X and Y bosons couple quarks to leptons, allowing violation of the...
are predicted to mediate the coupling of the electroweak and strong forces, but these particles are extremely heavy and well beyond the capabilities of any reasonable particle accelerator
Particle accelerator
A particle accelerator is a device that uses electromagnetic fields to propel charged particles to high speeds and to contain them in well-defined beams. An ordinary CRT television set is a simple form of accelerator. There are two basic types: electrostatic and oscillating field accelerators.In...
to create.
Searches for magnetic monopoles
A number of attempts have been made to detect magnetic monopoles. One of the simpler ones is to use a loop of superconducting wire to look for even tiny magnetic sources, a so-called "superconducting quantum interference device", or SQUIDSQUID
A SQUID is a very sensitive magnetometer used to measure extremely weak magnetic fields, based on superconducting loops containing Josephson junctions....
. Given the predicted density, loops small enough to fit on a lab bench would expect to see about one monopole event per year. Although there have been tantalizing events recorded, in particular the event recorded by Blas Cabrera
Blas Cabrera
Blas Cabrera is a physicist at Stanford University best known for his experiment in search of magnetic monopoles. He is the son of Spanish physicist Nicolás Cabrera and the grandson of the Blas Cabrera Felipe, also a Spanish physicist....
on the night of February 14, 1982 (thus, sometimes referred to as the "Valentine's Day Monopole"), there has never been reproducible evidence for the existence of magnetic monopoles. The lack of such events places a limit on the number of monopoles of about one monopole per 1029 nucleon
Nucleon
In physics, a nucleon is a collective name for two particles: the neutron and the proton. These are the two constituents of the atomic nucleus. Until the 1960s, the nucleons were thought to be elementary particles...
s.
Another experiment in 1975 resulted in the announcement of the detection of a moving magnetic monopole in cosmic ray
Cosmic ray
Cosmic rays are energetic charged subatomic particles, originating from outer space. They may produce secondary particles that penetrate the Earth's atmosphere and surface. The term ray is historical as cosmic rays were thought to be electromagnetic radiation...
s by the team led by P. Buford Price
P. Buford Price
Paul Buford Price, usually known as P. Buford Price, is a professor in the Graduate School at the University of California, Berkeley and a member of the National Academy of Sciences...
. Price later retracted his claim, and a possible alternative explanation was offered by Alvarez. In his paper it was demonstrated that the path of the cosmic ray event that was claimed to have been be due to a magnetic monopole could be reproduced by the path followed by a platinum
Platinum
Platinum is a chemical element with the chemical symbol Pt and an atomic number of 78. Its name is derived from the Spanish term platina del Pinto, which is literally translated into "little silver of the Pinto River." It is a dense, malleable, ductile, precious, gray-white transition metal...
nucleus decaying first to osmium
Osmium
Osmium is a chemical element with the symbol Os and atomic number 76. Osmium is a hard, brittle, blue-gray or blue-blacktransition metal in the platinum family, and is the densest natural element. Osmium is twice as dense as lead. The density of osmium is , slightly greater than that of iridium,...
, and then to tantalum
Tantalum
Tantalum is a chemical element with the symbol Ta and atomic number 73. Previously known as tantalium, the name comes from Tantalus, a character in Greek mythology. Tantalum is a rare, hard, blue-gray, lustrous transition metal that is highly corrosion resistant. It is part of the refractory...
.
Other experiments rely on the strong coupling of monopoles with photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s, as is the case for any electrically-charged particle as well. In experiments involving photon exchange in particle accelerators, monopoles should be produced in reasonable numbers, and detected due to their effect on the scattering of the photons. The probability of a particle being created in such experiments is related to their mass — with heavier particles being less likely to be created — so by examining the results of such experiments, limits on the mass of a magnetic monopole can be calculated. The most recent such experiments suggest that monopoles with masses below do not exist, while upper limits on their mass due to the very existence of the universe - which would have collapsed by now if they were too heavy - are about 1017 .
The MoEDAL experiment
MoEDAL experiment
The Monopole and Exotics Detector At the LHC is an international research collaboration whose spokesperson is the University of Alberta’s James Pinfold. MoEDAL is the seventh experiment at the LHC; it was approved and sanctioned by the CERN research board on May of 2010, and started its first test...
, installed at the Large Hadron Collider
Large Hadron Collider
The Large Hadron Collider is the world's largest and highest-energy particle accelerator. It is expected to address some of the most fundamental questions of physics, advancing the understanding of the deepest laws of nature....
, is currently searching for magnetic monopoles and large supersymmetric particles using layers of special plastic sheets attached to the walls around LHCb
LHCb
LHCb is one of six particle physics detector experiments collecting data at the Large Hadron Collider accelerator at CERN. LHCb is a specialized b-physics experiment, that is measuring the parameters of CP violation in the interactions of b-hadrons...
's VELO detector. The particles it is looking for will damage the sheets along their path, with various identifying features.
"Monopoles" in condensed-matter systems
While a magnetic monopole particleElementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
has never been conclusively observed, there are a number of phenomena in condensed-matter physics where a material, due to the collective behavior of its electrons and ions, can show emergent phenomena that resemble magnetic monopoles in some respect. These should not be confused with actual monopole particles: since all known particles have zero magnetic charge (including the proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
s, neutron
Neutron
The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
s, and electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s that make up the whole periodic table
Periodic table
The periodic table of the chemical elements is a tabular display of the 118 known chemical elements organized by selected properties of their atomic structures. Elements are presented by increasing atomic number, the number of protons in an atom's atomic nucleus...
), it is fundamentally impossible to find a true magnetic monopole in ordinary matter made from atoms; only quasiparticle
Quasiparticle
In physics, quasiparticles are emergent phenomena that occur when a microscopically complicated system such as a solid behaves as if it contained different weakly interacting particles in free space...
s are possible. In particular, the law ∇⋅B=0 is true everywhere in these systems, which it would not be in the presence of a true magnetic monopole particle. The Dirac string
Dirac string
In physics, a Dirac string is a fictitious one-dimensional curve in space, conceived of by the physicist Paul Dirac, stretching between two Dirac magnetic monopoles with opposite magnetic charges, or from one magnetic monopole out to infinity. The gauge potential cannot be defined on the Dirac...
model describes such a system in the theoretical limit of infinitely thin connecting fluxtubes.
One example of the work on magnetic monopole quasiparticles is a paper published in the journal Science
Science (journal)
Science is the academic journal of the American Association for the Advancement of Science and is one of the world's top scientific journals....
in September 2009, in which researchers Jonathan Morris and Alan Tennant from the Helmholtz-Zentrum Berlin für Materialien und Energie
Helmholtz-Zentrum Berlin
The Helmholtz-Zentrum Berlin for Materials and Energy is a research centre and part of the Helmholtz Association of German Research Centres. The institute carries out research into the structure and dynamics of novel materials and also investigates solar cell technology.Several large scale...
(HZB) along with Santiago Grigera from Instituto de Física de Líquidos y Sistemas Biológicos (IFLYSIB, CONICET) and other colleagues from Dresden University of Technology
Dresden University of Technology
The Technische Universität Dresden is the largest institute of higher education in the city of Dresden, the largest university in Saxony and one of the 10 largest universities in Germany with 36,066 students...
, University of St. Andrews and Oxford University described the observation of quasiparticle
Quasiparticle
In physics, quasiparticles are emergent phenomena that occur when a microscopically complicated system such as a solid behaves as if it contained different weakly interacting particles in free space...
s resembling magnetic monopoles. A single crystal of dysprosium titanate
Dysprosium titanate
Dysprosium titanate is an inorganic compound, a ceramic of the titanate family, with pyrochlore structure. Its CAS number is .Dysprosium titanate, like holmium titanate and holmium stannate, is a spin ice material...
in a highly frustrated pyrochlore lattice
Pyrochlore
Pyrochlore 2Nb2O6 is a solid solution between the niobium end member , and the tantalum end member .-Occurrence:...
(F d -3 m) was cooled to a temperature between 0.6 kelvin
Kelvin
The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
and 2.0 kelvin. Using observations of neutron scattering
Neutron scattering
Neutron scattering,the scattering of free neutrons by matter,is a physical processand an experimental technique using this processfor the investigation of materials.Neutron scattering as a physical process is of primordial importance...
, the magnetic moments were shown to align in the spin ice
Spin ice
A spin ice is a substance that is similar to water ice in that it can never be completely frozen. This is because it does not have a single minimal-energy state. A spin ice has "spin" degrees of freedom , with frustrated interactions which prevent it freezing...
into interwoven tubelike bundles resembling Dirac string
Dirac string
In physics, a Dirac string is a fictitious one-dimensional curve in space, conceived of by the physicist Paul Dirac, stretching between two Dirac magnetic monopoles with opposite magnetic charges, or from one magnetic monopole out to infinity. The gauge potential cannot be defined on the Dirac...
s. At the defect
Crystallographic defect
Crystalline solids exhibit a periodic crystal structure. The positions of atoms or molecules occur on repeating fixed distances, determined by the unit cell parameters. However, the arrangement of atom or molecules in most crystalline materials is not perfect...
formed by the end of each tube, the magnetic field looks like that of a monopole. Using an applied magnetic field to break the symmetry of the system, the researchers were able to control the density and orientation of these strings. A contribution to the heat capacity
Heat capacity
Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...
of the system from an effective gas of these quasiparticles was also described.
Another example of the work on magnetic monopole quasiparticles is a paper in the February 11, 2011 issue of Nature Physics
Nature Physics
Nature Physics, is a monthly, peer reviewed, scientific journal published by the Nature Publishing Group. It was first published in October 2005 . The Chief Editor is Alison Wright, who is a full-time professional editor employed by this journal...
which describes creation and measurement of long-lived magnetic monopole quasiparticle currents in spin ice. By applying a magnetic-field pulse to a dysprosium titanate (Dy2Ti2O7)
Dysprosium titanate
Dysprosium titanate is an inorganic compound, a ceramic of the titanate family, with pyrochlore structure. Its CAS number is .Dysprosium titanate, like holmium titanate and holmium stannate, is a spin ice material...
spin-ice crystal at 0.36 K, the authors created a relaxing magnetic current that lasted for several minutes. They measured the current by means of the electromotive force it induced in a solenoid coupled to a sensitive amplifier, and quantitatively described it using a chemical kinetic model of point-like charges obeying the Onsager–Wien mechanism of carrier dissociation and recombination. They thus derived the microscopic parameters of monopole motion in spin ice and identified the distinct roles of free and bound magnetic charges.
See also
- Dirac stringDirac stringIn physics, a Dirac string is a fictitious one-dimensional curve in space, conceived of by the physicist Paul Dirac, stretching between two Dirac magnetic monopoles with opposite magnetic charges, or from one magnetic monopole out to infinity. The gauge potential cannot be defined on the Dirac...
- DyonDyonIn physics, a dyon is a hypothetical particle in 4-dimensional theories with both electric and magnetic charges. A dyon with a zero electric charge is usually referred to as a magnetic monopole. Many grand unified theories predict the existence of both magnetic monopoles and dyons.Dyons were first...
- Felix EhrenhaftFelix EhrenhaftFelix Ehrenhaft was an Austrian physicist who contributed to atomic physics, to the measurement of electrical charges and to the optical properties of metal colloids. He was known for his maverick and controversial style...
- Gauss's law for magnetism
- Halbach arrayHalbach arrayA Halbach array is a special arrangement of permanent magnets that augments the magnetic field on one side of the array while cancelling the field to near zero on the other side...
- InstantonInstantonAn instanton is a notion appearing in theoretical and mathematical physics. Mathematically, a Yang–Mills instanton is a self-dual or anti-self-dual connection in a principal bundle over a four-dimensional Riemannian manifold that plays the role of physical space-time in non-abelian gauge theory...
- MeronMeronA meron or half-instanton is a Euclidean space-time solution of the Yang-Mills field equations. It is a singular non-self-dual solution of topological charge 1/2. The instanton is believed to be composed of two merons....
- Soliton
- 't Hooft–Polyakov monopole
- Wu–Yang monopole
External links
- Magnetic Monopole Searches (lecture notes)
- Particle Data Group summary of magnetic monopole search
- 'Race for the Pole' Dr David Milstead Freeview 'Snapshot' video by the Vega Science Trust and the BBC/OU.
- Interview with Jonathan Morris about magnetic monopoles and magnetic monopole quasiparticles. Drillingsraum, 16 April 2010