Seiberg duality
Encyclopedia
In quantum field theory
, Seiberg duality, conjectured by Nathan Seiberg
, is an S-duality
relating two different supersymmetric QCDs
. The two theories are not identical, but they agree at low energies. More precisely under a renormalization
group flow they flow to the same IR fixed point, and so are in the same universality class.
It was first presented in Seiberg's 1994 article Electric-Magnetic Duality in Supersymmetric Non-Abelian Gauge Theories. It is an extension to nonabelian
gauge theories
with N=1 supersymmetry of Montonen-Olive duality
in N=4 theories and electromagnetic duality in abelian
theories.
chiral multiplet
s and Nf flavors of antifundamental chiral multiplets in the chiral limit (no bare masses) and an N=1 chiral QCD with Nf-Nc colors and Nf flavors, where Nc and Nf are positive integers satisfying
A stronger version of the duality relates not only the chiral limit but also the full deformation space of the theory. In the special case in which
the IR fixed point is a nontrivial interacting superconformal field theory
. For a superconformal field theory, the anomalous scaling dimension
of a chiral superfield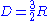
where R is the R-charge. This is an exact result.
The dual theory contains a fundamental "meson" chiral superfield M which is color neutral but transforms as a bifundamental under the flavor symmetries.
The dual theory contains the superpotential
.
s) with chromomagnetic fields (gluons of the dual gauge group), and chromoelectric charges (quark
s) with nonabelian 't Hooft-Polyakov monopole
s. In particular, the Higgs phase
is dual to the confinement
phase as in the dual superconducting model
.
The meson
s and baryon
s are preserved by the duality. However in the electric theory the meson is a quark bilinear (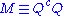
), while in the magnetic theory it is a fundamental field. In both theories the baryons are constructed from quarks, but the number of quarks in one baryon is the rank of the gauge group, which differs in the two dual theories.
The gauge symmetries of the theories do not agree, which is not problematic as the gauge symmetry is a feature of the formulation and not of the fundamental physics. The global symmetries
relate distinct physical configurations and so they need to agree in any dual description.
s of the dual theories are identical.
The global symmetries agree, as do the charges of the mesons and baryons.
In certain cases it reduces to ordinary electromagnetic duality.
It may be embedded in string theory
via Hanany-Witten brane cartoons consisting of intersecting D-brane
s. There it is realized as the motion of an NS5-brane
which is conjectured to preserve the universality class.
Six nontrivial anomalies may be computed on both sides of the duality, and they agree as they must in accordance with Gerard 't Hooft's anomaly matching condition
s. The role of the additional fundamental meson superfield M in the dual theory is very crucial in matching the anomalies. The global gravitational anomalies also match up as the parity of the number of chiral fields is the same in both theories. The R-charge of the Weyl fermion in a chiral superfield is one less than the R-charge of the superfield. The R-charge of a gaugino is +1.
, in which the flavor symmetries are also gauged. The simplest of these is a super QCD with the flavor group gauged and an additional term in the superpotential
. It leads to a series of Seiberg dualities known as a duality cascade. It was introduced by Matthew Strassler and Igor Klebanov
in Supergravity and a Confining Gauge Theory: Duality Cascades and
SB-Resolution of Naked Singularities.
It is not known whether Seiberg duality exists in 3-dimensional nonabelian gauge theories with only 4 supercharges, although a conjecture has appeared in Fractional M2-branes in some special cases with Chern-Simons
terms.
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, Seiberg duality, conjectured by Nathan Seiberg
Nathan Seiberg
Nathan "Nati" Seiberg is an Israeli American theoretical physicist who works on string theory. He was recipient of a 1996 MacArthur Fellowship and the Dannie Heineman Prize for Mathematical Physics in 1998. He is currently a professor at the Institute for Advanced Study in Princeton, New Jersey, USA...
, is an S-duality
S-duality
In theoretical physics, S-duality is an equivalence of two quantum field theories or string theories. An S-duality transformation maps states and vacua with coupling constant g in one theory to states and vacua with coupling constant 1/g in the dual theory...
relating two different supersymmetric QCDs
Super QCD
In theoretical physics, super QCD is a supersymmetric gauge theory which resembles quantum chromodynamics but contains additional particles and interactions which render it supersymmetric....
. The two theories are not identical, but they agree at low energies. More precisely under a renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
group flow they flow to the same IR fixed point, and so are in the same universality class.
It was first presented in Seiberg's 1994 article Electric-Magnetic Duality in Supersymmetric Non-Abelian Gauge Theories. It is an extension to nonabelian
Nonabelian group
In mathematics, a non-abelian group, also sometimes called a non-commutative group, is a group in which there are at least two elements a and b of G such that a * b ≠ b * a...
gauge theories
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
with N=1 supersymmetry of Montonen-Olive duality
Montonen-Olive duality
In theoretical physics, Montonen–Olive duality is the oldest known example of S-duality or a strong-weak duality. It generalizes the electro-magnetic symmetry of Maxwell's equations...
in N=4 theories and electromagnetic duality in abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
theories.
The statement of Seiberg duality
Seiberg duality is an equivalence of the IR fixed points in an N=1 theory with SU(Nc) as the gauge group and Nf flavors of fundamentalFundamental representation
In representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group...
chiral multiplet
Chiral superfield
In theoretical physics, one often analyzes theories with supersymmetry in which chiral superfields play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using the notion of superspace...
s and Nf flavors of antifundamental chiral multiplets in the chiral limit (no bare masses) and an N=1 chiral QCD with Nf-Nc colors and Nf flavors, where Nc and Nf are positive integers satisfying
-
.
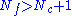A stronger version of the duality relates not only the chiral limit but also the full deformation space of the theory. In the special case in which
the IR fixed point is a nontrivial interacting superconformal field theory
Superconformal algebra
In theoretical physics, the superconformal algebra is a graded Lie algebra or superalgebra that combines the conformal algebra and supersymmetry. It generates the superconformal group in some cases .In two dimensions, the superconformal algebra is infinite-dimensional...
. For a superconformal field theory, the anomalous scaling dimension
Anomalous scaling dimension
In theoretical physics, by anomaly one usually means that the symmetry remains broken when the symmetry-breaking factor goes to zero.When the symmetry which is broken is scale invariance, then true power laws usually cannot be found from dimensional reasoning like in turbulence or quantum field...
of a chiral superfield
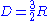where R is the R-charge. This is an exact result.The dual theory contains a fundamental "meson" chiral superfield M which is color neutral but transforms as a bifundamental under the flavor symmetries.
| SQCD | dual theory | |
|---|---|---|
| color gauge group |  |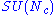
 |
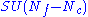| global internal symmetries |  |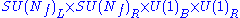
 |
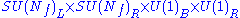| chiral superfields |  |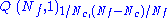
 |
 |
 |
|
 |
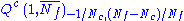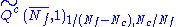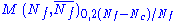The dual theory contains the superpotential
Superpotential
Superpotential is a concept from particle physics' supersymmetry.-Example of superpotentiality:Let's look at the example of a one dimensional nonrelativistic particle with a 2D internal degree of freedom called "spin"...
.Relations between the original and dual theories
Being an S-duality, Seiberg duality relates the strong coupling regime with the weak coupling regime, and interchanges chromoelectric fields (gluonGluon
Gluons are elementary particles which act as the exchange particles for the color force between quarks, analogous to the exchange of photons in the electromagnetic force between two charged particles....
s) with chromomagnetic fields (gluons of the dual gauge group), and chromoelectric charges (quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
s) with nonabelian 't Hooft-Polyakov monopole
't Hooft-Polyakov monopole
In theoretical physics, the t Hooft–Polyakov monopole is a topological soliton similar to the Dirac monopole but without any singularities. It arises in the case of a Yang–Mills theory with a gauge group G, coupled to a Higgs field which spontaneously breaks it down to a smaller group H via the...
s. In particular, the Higgs phase
Higgs phase
In theoretical physics, it is often important to consider gauge theory that admits many physical phenomena and "phases", connected by phase transitions, in which the vacuum may be found.Gauge symmetry may be broken by the Higgs mechanism...
is dual to the confinement
Colour confinement
Color confinement, often simply called confinement, is the physics phenomenon that color charged particles cannot be isolated singularly, and therefore cannot be directly observed. Quarks, by default, clump together to form groups, or hadrons. The two types of hadrons are the mesons and the baryons...
phase as in the dual superconducting model
Dual superconducting model
In the theory of quantum chromodynamics, dual superconductor models attempt to explain confinement of quarks in terms of an electromagnetic dual theory of superconductivity....
.
The meson
Meson
In particle physics, mesons are subatomic particles composed of one quark and one antiquark, bound together by the strong interaction. Because mesons are composed of sub-particles, they have a physical size, with a radius roughly one femtometer: 10−15 m, which is about the size of a proton...
s and baryon
Baryon
A baryon is a composite particle made up of three quarks . Baryons and mesons belong to the hadron family, which are the quark-based particles...
s are preserved by the duality. However in the electric theory the meson is a quark bilinear (
), while in the magnetic theory it is a fundamental field. In both theories the baryons are constructed from quarks, but the number of quarks in one baryon is the rank of the gauge group, which differs in the two dual theories.The gauge symmetries of the theories do not agree, which is not problematic as the gauge symmetry is a feature of the formulation and not of the fundamental physics. The global symmetries
Global symmetry
A global symmetry is a symmetry that holds at all points in the spacetime under consideration, as opposed to a local symmetry which varies from point to point.Global symmetries require conservation laws, but not forces, in physics.-See also:...
relate distinct physical configurations and so they need to agree in any dual description.
Evidence for Seiberg duality
The moduli spaceModuli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
s of the dual theories are identical.
The global symmetries agree, as do the charges of the mesons and baryons.
In certain cases it reduces to ordinary electromagnetic duality.
It may be embedded in string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
via Hanany-Witten brane cartoons consisting of intersecting D-brane
D-brane
In string theory, D-branes are a class of extended objects upon which open strings can end with Dirichlet boundary conditions, after which they are named. D-branes were discovered by Dai, Leigh and Polchinski, and independently by Hořava in 1989...
s. There it is realized as the motion of an NS5-brane
NS5-brane
In theoretical physics, the NS5-brane is a five-dimensional object in string theory that carries a magnetic charge under the B-field, the field under which the fundamental string is electrically charged....
which is conjectured to preserve the universality class.
Six nontrivial anomalies may be computed on both sides of the duality, and they agree as they must in accordance with Gerard 't Hooft's anomaly matching condition
Anomaly matching condition
In quantum field theory, the anomaly matching condition by Gerard 't Hooft states that the calculation of any chiral anomaly by using the degrees of freedom of the theory at some energy scale, must not depend on what scale is chosen for the calculation...
s. The role of the additional fundamental meson superfield M in the dual theory is very crucial in matching the anomalies. The global gravitational anomalies also match up as the parity of the number of chiral fields is the same in both theories. The R-charge of the Weyl fermion in a chiral superfield is one less than the R-charge of the superfield. The R-charge of a gaugino is +1.
| anomaly | SQCD | dual theory |
|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
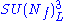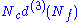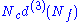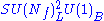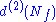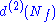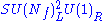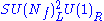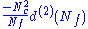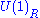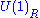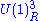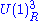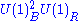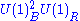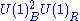Generalizations
Seiberg duality has been generalized in many directions. One generalization applies to quiver gauge theoriesQuiver diagram
In physics, a quiver diagram is a graph representing the matter content of a gauge theory that describes D-branes on orbifolds.Each node of the graph corresponds to a factor U of the gauge group, and each link represents a field in the bifundamental representation.The relevance of quiver diagrams...
, in which the flavor symmetries are also gauged. The simplest of these is a super QCD with the flavor group gauged and an additional term in the superpotential
Superpotential
Superpotential is a concept from particle physics' supersymmetry.-Example of superpotentiality:Let's look at the example of a one dimensional nonrelativistic particle with a 2D internal degree of freedom called "spin"...
. It leads to a series of Seiberg dualities known as a duality cascade. It was introduced by Matthew Strassler and Igor Klebanov
Igor Klebanov
Igor R. Klebanov is a theoretical physicist whose research is centered on relations between string theory and quantum gauge field theory. Since 1989, he has been a Professor at Princeton University....
in Supergravity and a Confining Gauge Theory: Duality Cascades and
SB-Resolution of Naked Singularities.It is not known whether Seiberg duality exists in 3-dimensional nonabelian gauge theories with only 4 supercharges, although a conjecture has appeared in Fractional M2-branes in some special cases with Chern-Simons
Chern-Simons theory
The Chern–Simons theory is a 3-dimensional topological quantum field theory of Schwarz type, introduced by Edward Witten. It is so named because its action is proportional to the integral of the Chern–Simons 3-form....
terms.