Mu problem
Encyclopedia
In theoretical physics, the μ problem is a problem of supersymmetric
theories, concerned with understanding the parameters of the theory.
The supersymmetric Higgs
mass parameter μ appears as the following term in the superpotential
: μHuHd. It is necessary to provide a mass for the fermionic superpartners of the Higgs bosons, i.e. the higgsinos, and it enters as well the scalar potential of the Higgs bosons. To ensure that Hu and Hd get a non-zero vacuum expectation value
after electroweak symmetry breaking, μ should be of the order of magnitude of the electroweak scale, many orders of magnitude smaller than the Planck scale
, which is the natural cutoff
scale.
The soft supersymmetry breaking terms should also be of the same order of magnitude as the electroweak scale. This brings about a problem of naturalness
: why are these scales so much smaller than the cutoff scale? And why, if the soft supersymmetry breaking terms and the μ term in the superpotential have different physical origins, do the corresponding scales happen to fall so close to each other?
One proposed solution is that this term does not appear explicitly in the Lagrangian, because it violates some global symmetry, and can therefore be created only via spontaneous breaking
of this symmetry. This is proposed to happen together with F-term
supersymmetry breaking
, with a spurious field X that parameterizes the hidden supersymmetry-breaking sector of the theory (meaning that FX is the non-zero F-term). Let us assume that the Kahler potential includes a term of the form
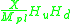times some dimensionless coefficient which is naturally of order one where Mpl is Planck mass. Then as supersymmetry breaks, FX gets a non-zero vacuum expectation value X> and the following effective term is added to the superpotential:
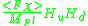, which gives a measured 
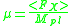. On the other hand, soft supersymmetry breaking terms are similarly created and also have a natural scale of 
.
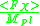Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
theories, concerned with understanding the parameters of the theory.
The supersymmetric Higgs
Higgs
The term Higgs appears in:* Alan Higgs, English businessman and philanthropist* Sir Derek Higgs, an English business leader and merchant banker* Eric Sidney Higgs, English archaeologist*Griffin Higgs...
mass parameter μ appears as the following term in the superpotential
Superpotential
Superpotential is a concept from particle physics' supersymmetry.-Example of superpotentiality:Let's look at the example of a one dimensional nonrelativistic particle with a 2D internal degree of freedom called "spin"...
: μHuHd. It is necessary to provide a mass for the fermionic superpartners of the Higgs bosons, i.e. the higgsinos, and it enters as well the scalar potential of the Higgs bosons. To ensure that Hu and Hd get a non-zero vacuum expectation value
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
after electroweak symmetry breaking, μ should be of the order of magnitude of the electroweak scale, many orders of magnitude smaller than the Planck scale
Planck scale
In particle physics and physical cosmology, the Planck scale is an energy scale around 1.22 × 1019 GeV at which quantum effects of gravity become strong...
, which is the natural cutoff
Cutoff
In theoretical physics, cutoff is an arbitrary maximal or minimal value of energy, momentum, or length, used in order that objects with larger or smaller values than these physical quantities are ignored in some calculation...
scale.
The soft supersymmetry breaking terms should also be of the same order of magnitude as the electroweak scale. This brings about a problem of naturalness
Naturalness (particle physics)
Naturalness is the property that all parameters appearing in a theory take values of order 1...
: why are these scales so much smaller than the cutoff scale? And why, if the soft supersymmetry breaking terms and the μ term in the superpotential have different physical origins, do the corresponding scales happen to fall so close to each other?
One proposed solution is that this term does not appear explicitly in the Lagrangian, because it violates some global symmetry, and can therefore be created only via spontaneous breaking
Spontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
of this symmetry. This is proposed to happen together with F-term
F-term
In theoretical physics, one often analyzes theories with supersymmetry in which F-terms play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using a superspace. This superspace involves four extra fermionic coordinates \theta^1,\theta^2,\bar\theta^1,\bar\theta^2,...
supersymmetry breaking
Supersymmetry breaking
In particle physics, supersymmetry breaking is the process to obtain a seemingly non-supersymmetric physics from a supersymmetric theory which is a necessary step to reconcile supersymmetry with actual experiments. It is an example of spontaneous symmetry breaking...
, with a spurious field X that parameterizes the hidden supersymmetry-breaking sector of the theory (meaning that FX is the non-zero F-term). Let us assume that the Kahler potential includes a term of the form
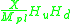times some dimensionless coefficient which is naturally of order one where Mpl is Planck mass. Then as supersymmetry breaks, FX gets a non-zero vacuum expectation value 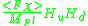, which gives a measured 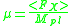. On the other hand, soft supersymmetry breaking terms are similarly created and also have a natural scale of 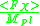.See also
- NMSSMNMSSMIn particle physics, NMSSM is an acronym for Next-to-Minimal Supersymmetric Standard Model. It is a supersymmetric extension to the Standard Model that adds an additional singlet chiral superfield to the MSSM and can be used to dynamically generate the \mu term, solving the mu problem.For review...
(Next-to-Minimal Supersymmetric Standard Model) - Minimal Supersymmetric Standard ModelMinimal Supersymmetric Standard ModelThe Minimal Supersymmetric Standard Model is the minimal extension to the Standard Model that realizes supersymmetry, although non-minimal extensions do exist. Supersymmetry pairs bosons with fermions; therefore every Standard Model particle has a partner that has yet to be discovered...