
Musical isomorphism
Encyclopedia
In mathematics
, the musical isomorphism (or canonical isomorphism) is an isomorphism
between the tangent bundle
TM and the cotangent bundle
T*M of a Riemannian manifold
given by its metric. There are similar isomorphisms on symplectic manifold
s.
It is also known as raising and lowering indices
.
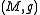 be a Riemannian manifold
be a Riemannian manifold
. Suppose is a local frame for the tangent bundle
is a local frame for the tangent bundle 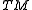 with dual coframe
with dual coframe  . Then, locally, we may express the Riemannian metric (which is a 2-covariant tensor field which is symmetric and positive-definite) as
. Then, locally, we may express the Riemannian metric (which is a 2-covariant tensor field which is symmetric and positive-definite) as 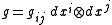 (where we employ the Einstein summation convention). Given a vector field
(where we employ the Einstein summation convention). Given a vector field 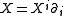 we define its flat by
we define its flat by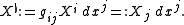
This is referred to as 'lowering an index'. Using the traditional diamond bracket notation for inner product defined by g, we obtain the somewhat more transparent relation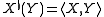
for all vectors X and Y.
Alternatively, given a covector field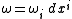 we define its sharp by
we define its sharp by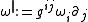
where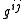 are the elements of the inverse matrix to
are the elements of the inverse matrix to 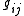 . Taking the sharp of a covector field is referred to as 'raising an index'.
. Taking the sharp of a covector field is referred to as 'raising an index'.
Through this construction we have two inverse isomorphisms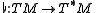 and
and  . These are isomorphisms of vector bundles and hence we have, for each
. These are isomorphisms of vector bundles and hence we have, for each 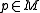 , inverse vector space isomorphisms between
, inverse vector space isomorphisms between 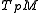 and
and 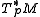 .
.
The musical isomorphisms may also be extended to the bundles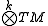 and
and  . It must be stated which index is to be raised or lowered. For instance, consider the (2,0) tensor field
. It must be stated which index is to be raised or lowered. For instance, consider the (2,0) tensor field 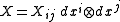 . Raising the second index, we get the (1,1) tensor field
. Raising the second index, we get the (1,1) tensor field 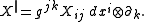
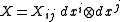 we define the trace of
we define the trace of 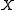 through the metric
through the metric 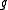 by
by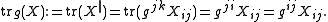
Observe that the definition of trace is independent of the choice of index we raise since the metric tensor is symmetric.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the musical isomorphism (or canonical isomorphism) is an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
between the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
TM and the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
T*M of a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
given by its metric. There are similar isomorphisms on symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
s.
It is also known as raising and lowering indices
Raising and lowering indices
In mathematics and mathematical physics, given a tensor on a manifold M, in the presence of a nonsingular form on M , one can raise or lower indices: change a type tensor to a tensor or to a tensor...
.
Discussion
Let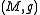 be a Riemannian manifold
be a Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
. Suppose
 is a local frame for the tangent bundle
is a local frame for the tangent bundle 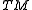 with dual coframe
with dual coframe  . Then, locally, we may express the Riemannian metric (which is a 2-covariant tensor field which is symmetric and positive-definite) as
. Then, locally, we may express the Riemannian metric (which is a 2-covariant tensor field which is symmetric and positive-definite) as 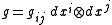 (where we employ the Einstein summation convention). Given a vector field
(where we employ the Einstein summation convention). Given a vector field 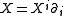 we define its flat by
we define its flat by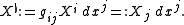
This is referred to as 'lowering an index'. Using the traditional diamond bracket notation for inner product defined by g, we obtain the somewhat more transparent relation
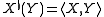
for all vectors X and Y.
Alternatively, given a covector field
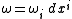 we define its sharp by
we define its sharp by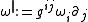
where
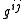 are the elements of the inverse matrix to
are the elements of the inverse matrix to 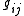 . Taking the sharp of a covector field is referred to as 'raising an index'.
. Taking the sharp of a covector field is referred to as 'raising an index'.Through this construction we have two inverse isomorphisms
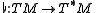 and
and  . These are isomorphisms of vector bundles and hence we have, for each
. These are isomorphisms of vector bundles and hence we have, for each 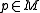 , inverse vector space isomorphisms between
, inverse vector space isomorphisms between 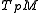 and
and 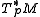 .
.The musical isomorphisms may also be extended to the bundles
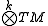 and
and  . It must be stated which index is to be raised or lowered. For instance, consider the (2,0) tensor field
. It must be stated which index is to be raised or lowered. For instance, consider the (2,0) tensor field 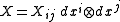 . Raising the second index, we get the (1,1) tensor field
. Raising the second index, we get the (1,1) tensor field 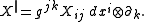
Trace of a tensor through a metric
Given a (2,0) tensor field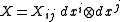 we define the trace of
we define the trace of 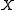 through the metric
through the metric 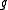 by
by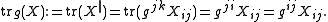
Observe that the definition of trace is independent of the choice of index we raise since the metric tensor is symmetric.
See also
- Duality (mathematics)Duality (mathematics)In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
- Raising and lowering indicesRaising and lowering indicesIn mathematics and mathematical physics, given a tensor on a manifold M, in the presence of a nonsingular form on M , one can raise or lower indices: change a type tensor to a tensor or to a tensor...
- Bilinear products and dual spaces
- Vector bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
- Flat (music) and Sharp (music)Sharp (music)In music, sharp, dièse , or diesis means higher in pitch and the sharp symbol raises a note by a half tone. Intonation may be flat, sharp, or both, successively or simultaneously...
about the signs and

