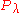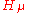N!-conjecture
Encyclopedia
In mathematics, the n! conjecture is the conjecture
that the dimension
of a certain bi-graded module
of diagonal harmonics is
. It was made by A. M. Garsia and M. Haiman and later proved by M. Haiman. It implies Macdonald
's positivity conjecture about his Macdonald polynomial
s.
s
are a two-parameter family of orthogonal polynomials
indexed by a positive weight λ of a root system
, introduced by Ian G. Macdonald
(1987). They generalize several other families of orthogonal polynomials, such as Jack polynomials and Hall–Littlewood polynomial
s. They are known to have deep relationships with affine Hecke algebra
s and Hilbert scheme
s, which were used to prove several conjectures made by Macdonald about them.
In 1988, Macdonald (see [5]) introduced a new basis for the space of symmetric function
s, which specializes to many of the well-known bases for the symmetric functions, by suitable substitutions for the parameters q and t.
In fact, we can obtain in this manner the Schur functions, the Hall–Littlewood symmetric functions, the Jack symmetric functions, the zonal symmetric functions, the zonal spherical function
s, and the elementary and monomial symmetric functions.
The so called (q,t)-Kostka polynomial
s are the coefficients of a resulting transition matrix. Macdonald conjectured that they are polynomials in q and t, with non-negative integer coefficients.
's idea to construct an appropriate module in order to prove positivity (as was done in his previous joint work with Procesi on Schur positivity of Kostka–Foulkes polynomials).
In an attempt to prove Macdonald's conjecture, Garsia and Haiman (see [2]) introduced the bi-graded module
of diagonal harmonics and conjectured that the (modified) Macdonald polynomials are the Frobenius image of the character generating function of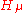
, under the diagonal action of the symmetric group
.
The proof of Macdonald's conjecture was then reduced to the n! conjecture; i.e., to prove that the dimension of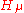
is n!. In 2001, Haiman proved that the dimension is indeed n! (see [4]). Thanks to this piece of work (Hilbert schemes played a key role in the solution) Haiman was named full professor in UC Berkeley.
This breakthrough led to the discovery of many hidden connections and new aspects of symmetric group representation theory, as well as combinatorial objects (e.g., insertion tableaux, Haglund's inversion numbers, the role of parking functions in representation theory etc. etc.).
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
that the dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
of a certain bi-graded module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
of diagonal harmonics is
. It was made by A. M. Garsia and M. Haiman and later proved by M. Haiman. It implies MacdonaldIan G. Macdonald
Ian Grant Macdonald is a British mathematician known for his contributions to symmetric functions, special functions, Lie algebra theory and other aspects of algebraic combinatorics ....
's positivity conjecture about his Macdonald polynomial
Macdonald polynomial
In mathematics, Macdonald polynomials Pλ are a family of orthogonal polynomials in several variables, introduced by...
s.
Formulation
The Macdonald polynomialMacdonald polynomial
In mathematics, Macdonald polynomials Pλ are a family of orthogonal polynomials in several variables, introduced by...
s
are a two-parameter family of orthogonal polynomials
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
indexed by a positive weight λ of a root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
, introduced by Ian G. Macdonald
Ian G. Macdonald
Ian Grant Macdonald is a British mathematician known for his contributions to symmetric functions, special functions, Lie algebra theory and other aspects of algebraic combinatorics ....
(1987). They generalize several other families of orthogonal polynomials, such as Jack polynomials and Hall–Littlewood polynomial
Hall–Littlewood polynomial
In mathematics, the Hall–Littlewood polynomials are symmetric functions depending on a parameter t and a partition λ. They are Schur functions when t is 0 and monomial symmetric functions when t is 1 and are special cases of Macdonald polynomials.They were first defined indirectly by ...
s. They are known to have deep relationships with affine Hecke algebra
Affine Hecke algebra
In mathematics, an affine Hecke algebra is the Hecke algebra of an affine Weyl group, and can be used to prove Macdonald's constant term conjecture for Macdonald polynomials.-Definition:...
s and Hilbert scheme
Hilbert scheme
In algebraic geometry, a branch of mathematics, a Hilbert scheme is a scheme that is the parameter space for the closed subschemes of some projective space , refining the Chow variety. The Hilbert scheme is a disjoint union of projective subschemes corresponding to Hilbert polynomials...
s, which were used to prove several conjectures made by Macdonald about them.
In 1988, Macdonald (see [5]) introduced a new basis for the space of symmetric function
Symmetric function
In algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
s, which specializes to many of the well-known bases for the symmetric functions, by suitable substitutions for the parameters q and t.
In fact, we can obtain in this manner the Schur functions, the Hall–Littlewood symmetric functions, the Jack symmetric functions, the zonal symmetric functions, the zonal spherical function
Zonal spherical function
In mathematics, a zonal spherical function or often just spherical function is a function on a locally compact group G with compact subgroup K that arises as the matrix coefficient of a K-invariant vector in an irreducible representation of G...
s, and the elementary and monomial symmetric functions.
The so called (q,t)-Kostka polynomial
Kostka polynomial
In mathematics, a Kostka polynomial or Kostka–Foulkes polynomial Kλμ, named after Carl Kostka, is a polynomial in two variables with non-negative integer coefficients depending on two partitions λ and μ...
s are the coefficients of a resulting transition matrix. Macdonald conjectured that they are polynomials in q and t, with non-negative integer coefficients.
The approach of Garsia and Haiman
It was Adriano GarsiaAdriano Garsia
Adriano Mario Garsia is an Italian American mathematician, a leading expert in combinatorics, representation theory, and algebraic geometry, a student of Charles Loewner. He has made many deep contributions to representation theory, symmetric functions and algebraic combinatorics, which exerted a...
's idea to construct an appropriate module in order to prove positivity (as was done in his previous joint work with Procesi on Schur positivity of Kostka–Foulkes polynomials).
In an attempt to prove Macdonald's conjecture, Garsia and Haiman (see [2]) introduced the bi-graded module
of diagonal harmonics and conjectured that the (modified) Macdonald polynomials are the Frobenius image of the character generating function of
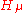, under the diagonal action of the symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
.
The proof of Macdonald's conjecture was then reduced to the n! conjecture; i.e., to prove that the dimension of
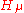is n!. In 2001, Haiman proved that the dimension is indeed n! (see [4]). Thanks to this piece of work (Hilbert schemes played a key role in the solution) Haiman was named full professor in UC Berkeley.This breakthrough led to the discovery of many hidden connections and new aspects of symmetric group representation theory, as well as combinatorial objects (e.g., insertion tableaux, Haglund's inversion numbers, the role of parking functions in representation theory etc. etc.).
External links
- Bourbaki seminar (Procesi), PDF
- n! conjecture by François Bergeron
- n! homepage of Garsia
- http://www.maths.ed.ac.uk/~igordon/pubs/grenoble3.pdf
- http://mathworld.wolfram.com/n!Theorem.html