Newtonian motivations for general relativity
Encyclopedia
Some of the basic concepts of General Relativity
can be outlined outside the relativistic
domain. In particular, the idea that mass/energy generates curvature
in space
and that curvature affects the motion of masses can be illustrated in a Newtonian setting. We use circular orbits as our prototype. This has the advantage that we know the kinetics of circular orbits. This allows us to calculate curvature of orbits in space directly and compare the results with dynamical forces.
. Objects move in spacetime along geodesics, the paths which yield the shortest distance between two points in spacetime.
polar
orbits of the earth
at radius
and speed 
. Since the orbits are circular, the gravitational force on the particles must equal the centripetal force
,
where G is the gravitational constant
and
is the mass
of the earth.
The particles execute simple harmonic motion
about the earth and with respect to each other. They are at their maximum distance from each other as they cross the equator. Their trajectories
intersect at the poles.
From Newton's Law of Gravitation the separation vector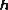
can be shown to be given by the "geodesic equation"
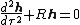
where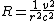
is the curvature
of the trajectory and
is the speed of light
c times the time.
The curvature of the trajectory is generated by the mass of the earth
. This is represented by the "field equation"
In this example, the field equation is simply a statement of the Newtonian concept that centripetal force is equal to gravitational force for circular orbits. We refer to this expression as a field equation in order to highlight the similarities with the Einstein field equation. This equation is in a much different form than Gauss's law
, which is the usual characterization of the field equation in Newtonian mechanics.
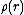inside a sphere of radius 
by the expression
.
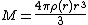The field equation becomes
.
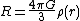The curvature of the particle trajectories is proportional to mass density.
of the spacecraft coincident with one of the particles. That particle would be at rest with respect to the spacecraft. An observer in the spacecraft would have no indication that the craft was orbiting the earth. The observer is only allowed to measure the behavior of the particles in the frame of the craft.
In this example, we can define a local coordinate system such that the
-direction is toward the ceiling of the craft and this is directed along 
. The 
-direction is toward the front of the craft and is in the direction of 
. The 
-direction is toward the left side of the craft.
In this frame, the vector
is the position vector for the second particle. An observer in the craft would think the second particle was oscillating in a potential well
generated by a gravitational field. This is an example of a coordinate acceleration
due to the choice of frames as opposed to a physical acceleration due to actual forces.
More generally, particles move in elliptic
or hyberbolic trajectories in a plane that contains the earth center. The orbits need not be circular
. One can obtain intuitive geodesic and field equations in those situations as well [Ref 2, Chapter 1]. Unlike circular orbits, however, the speed of the particles in elliptic or hyperbolic trajectories is not constant. We therefore do not have a constant speed with which to scale the curvature. Therefore, in anticipation of the transition to relativistic mechanics, the trajectories and curvatures are scaled with the speed of light
.
From Newton's Law of Gravitation
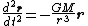
one can obtain the geodesic equation for the separation of two particles in nearby trajectories
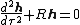
and the field equation
if the particle separation is perpendicular to
and
if the separation is parallel to
. In the calculation of 
the radius was expanded in terms of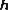 
. Only the linear
term was retained.
In the case that the separation of the particle is radial, the curvature is negative. This will cause the particles to separate rather than to be drawn toward each other as in the case in which they have the same radius. This is easy to understand. Outer orbits travel slower than inner orbits. This leads to particle separation.
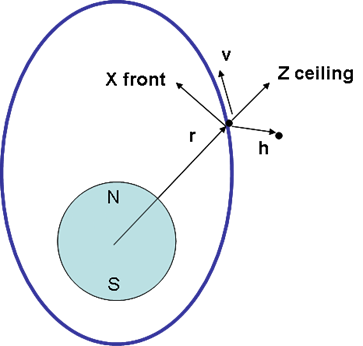A local coordinate system for a space craft co-moving with one of the particles can again be defined. The 
-direction, toward the ceiling, is in the direction of 
. The 
-direction, toward the front of the craft, is perpendicular to 
but still in the plane of the trajectory. Unlike in a circular orbit, this craft no longer necessarily points in the direction of the velocity. The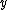 
-direction is toward the left side of the craft.
notation [Ref. 2, p. 37] in the co-moving frame in which the ceiling of the space craft is in the
direction
where the Latin indices are over the spatial directions in the co-moving system, and we have used the Einstein summation convention in which repeated indices are summed. The curvature tensor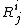
is given by
and the separation vector is given by
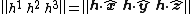
where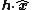
is the component of 
in the 
direction,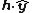 
is the component in the 
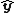direction, and 
is the component in the 
direction.
In this co-moving coordinate system the curvature tensor is diagonal. This is not true in general.
direction, nor can he/she know which direction is the velocity with respect to earth. The orientation of the spacecraft may be quite different from the simple coordinate system in which the ceiling is in the 
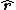direction and the front of the craft is in a direction coplanar with the radius and the velocity. We can transform our simple coordinates to an arbitrarily oriented coordinate system through rotations. This, however, destroys the diagonal nature of the curvature matrix.
Rotations are performed with a rotation matrix
such that the separation vector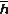 
is related to the separation vector before rotation 
by the relation
.
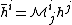The inverse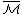
of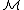 
is defined by
,
which yields
.
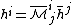Here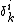
is the Kronecker delta.
A simple rotation matrix that rotates the coordinate axis through an angle
about the 
-axis is
.
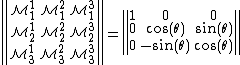This is a rotation in the y-z plane. The inverse is obtained by switching the sign of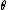
.
If the rotation matrix does not depend on time then the geodisic equation becomes, upon rotation
where
.
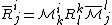The curvature in the new coordinate system is non-diagonal. The inverse problem of transforming an arbitray coordinate system into a diagonal system can be performed mathematically with the process of diagonalization
.
In that case, the rotation of the separation velocity can be written
which becomes
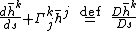
where
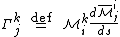
is known as a Christoffel symbol.
The geodesic equation becomes
,
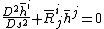which is the same as before with the exception that the derivatives have been generalized.
.
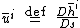The geodesic equation becomes
.
.
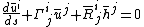In an arbitrarily rotating spacecraft, the curvature of space is due to two terms, one due to the mass density and one due to the arbitrary rotation of the spacecraft. The arbitrary rotation is non-physical and must be eliminated in any real physical theory of gravitation. In General Relativity this is done with a process called Fermi-Walker transport
. In a Euclidean
sense, Fermi-Walker transport is simply a statement that the spacecraft is not allowed to tumble
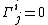
for all i and j. The only time-dependent rotations allowed are those generated by the mass density.
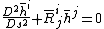
where
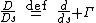
and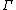
is a Christoffel symbol.
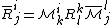
where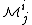
is a rotation matrix and the curvature tensor is
.
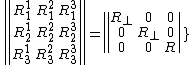The curvature is proportional to the mass density
.
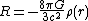s, Christoffel symbols, and Fermi-Walker transport
.
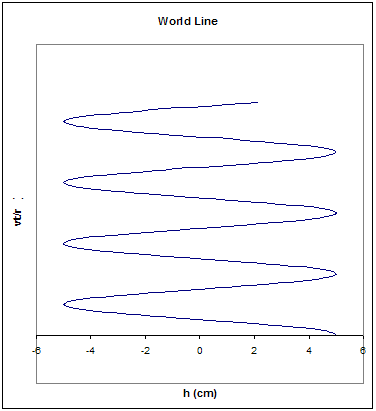
General relativity generalizes the geodesic equation and the field equation to the relativistic realm in which trajectories in space are replaced with world line
s in spacetime
. The equations are also generalized to more complicated curvatures.
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
can be outlined outside the relativistic
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
domain. In particular, the idea that mass/energy generates curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
in space
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
and that curvature affects the motion of masses can be illustrated in a Newtonian setting. We use circular orbits as our prototype. This has the advantage that we know the kinetics of circular orbits. This allows us to calculate curvature of orbits in space directly and compare the results with dynamical forces.
The equivalence of gravitational and inertial mass
A unique feature of the gravitational force is that all massive objects accelerate in the same manner in a gravitational field. This is often expressed as "The gravitational mass is equal to the inertial mass." This allows us to think of gravity as a curvature of spacetimeSpacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
. Objects move in spacetime along geodesics, the paths which yield the shortest distance between two points in spacetime.
Test for flatness in spacetime
If initially parallel paths of two particles on nearby geodesics remain parallel within some accuracy, then spacetime is flat to within that accuracy. [Ref. 2, p. 30]Newtonian mechanics for circular orbits
The geodesic and field equations for circular orbits
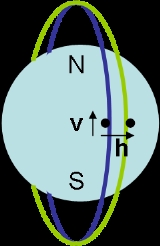
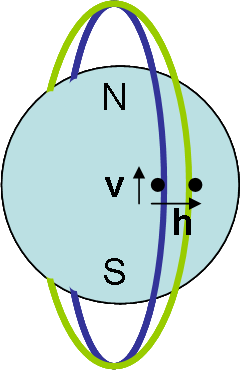
Consider the situation in which there are two particles in nearby circularCircular orbit
A circular orbit is the orbit at a fixed distance around any point by an object rotating around a fixed axis.Below we consider a circular orbit in astrodynamics or celestial mechanics under standard assumptions...
polar
Polar orbit
A polar orbit is an orbit in which a satellite passes above or nearly above both poles of the body being orbited on each revolution. It therefore has an inclination of 90 degrees to the equator...
orbits of the earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
at radius
and speed . Since the orbits are circular, the gravitational force on the particles must equal the centripetal forceCentripetal force
Centripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...
,
where G is the gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
and
is the massMass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
of the earth.
The particles execute simple harmonic motion
Simple harmonic motion
Simple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....
about the earth and with respect to each other. They are at their maximum distance from each other as they cross the equator. Their trajectories
Trajectory
A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...
intersect at the poles.
From Newton's Law of Gravitation the separation vector
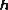can be shown to be given by the "geodesic equation"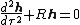where
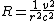is the curvatureCurvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of the trajectory and
is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
c times the time.
The curvature of the trajectory is generated by the mass of the earth
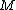. This is represented by the "field equation"In this example, the field equation is simply a statement of the Newtonian concept that centripetal force is equal to gravitational force for circular orbits. We refer to this expression as a field equation in order to highlight the similarities with the Einstein field equation. This equation is in a much different form than Gauss's law
Gauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
, which is the usual characterization of the field equation in Newtonian mechanics.
Relationship between curvature and mass density
Mass can be written in terms of the average mass density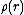 inside a sphere of radius by the expression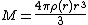.The field equation becomes
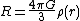.The curvature of the particle trajectories is proportional to mass density.
Local measurements
A requirement of General Relativity is that all measurements must be made locally. We can therefore imagine that the particles are inside a windowless spacecraft co-orbiting the earth with the center of massCenter of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
of the spacecraft coincident with one of the particles. That particle would be at rest with respect to the spacecraft. An observer in the spacecraft would have no indication that the craft was orbiting the earth. The observer is only allowed to measure the behavior of the particles in the frame of the craft.
In this example, we can define a local coordinate system such that the
-direction is toward the ceiling of the craft and this is directed along . The -direction is toward the front of the craft and is in the direction of . The -direction is toward the left side of the craft.In this frame, the vector
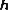is the position vector for the second particle. An observer in the craft would think the second particle was oscillating in a potential wellPotential well
A potential well is the region surrounding a local minimum of potential energy. Energy captured in a potential well is unable to convert to another type of energy because it is captured in the local minimum of a potential well...
generated by a gravitational field. This is an example of a coordinate acceleration
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
due to the choice of frames as opposed to a physical acceleration due to actual forces.
Elliptic and hyberbolic trajectories
Elliptic orbit
In astrodynamics or celestial mechanics an elliptic orbit is a Kepler orbit with the eccentricity less than 1; this includes the special case of a circular orbit, with eccentricity equal to zero. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1 . In a...
or hyberbolic trajectories in a plane that contains the earth center. The orbits need not be circular
Circular orbit
A circular orbit is the orbit at a fixed distance around any point by an object rotating around a fixed axis.Below we consider a circular orbit in astrodynamics or celestial mechanics under standard assumptions...
. One can obtain intuitive geodesic and field equations in those situations as well [Ref 2, Chapter 1]. Unlike circular orbits, however, the speed of the particles in elliptic or hyperbolic trajectories is not constant. We therefore do not have a constant speed with which to scale the curvature. Therefore, in anticipation of the transition to relativistic mechanics, the trajectories and curvatures are scaled with the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
.From Newton's Law of Gravitation
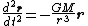
one can obtain the geodesic equation for the separation of two particles in nearby trajectories
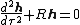
and the field equation
if the particle separation is perpendicular to
andif the separation is parallel to
. In the calculation of the radius was expanded in terms of 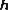. Only the linearLinear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
term was retained.
In the case that the separation of the particle is radial, the curvature is negative. This will cause the particles to separate rather than to be drawn toward each other as in the case in which they have the same radius. This is easy to understand. Outer orbits travel slower than inner orbits. This leads to particle separation.
Local coordinate system
-direction, toward the ceiling, is in the direction of . The -direction, toward the front of the craft, is perpendicular to but still in the plane of the trajectory. Unlike in a circular orbit, this craft no longer necessarily points in the direction of the velocity. The -direction is toward the left side of the craft.Simple diagonal frame
The geodesic equation in a radial gravitational field can be described succinctly in tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
notation [Ref. 2, p. 37] in the co-moving frame in which the ceiling of the space craft is in the
directionwhere the Latin indices are over the spatial directions in the co-moving system, and we have used the Einstein summation convention in which repeated indices are summed. The curvature tensor
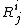is given byand the separation vector is given by
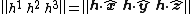
where
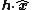is the component of in the direction, 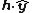is the component in the 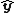direction, and is the component in the direction.In this co-moving coordinate system the curvature tensor is diagonal. This is not true in general.
Arbitrary orientation of the local frame
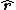The co-moving spacecraft has no windows. An observer is not able to tell which direction is the direction, nor can he/she know which direction is the velocity with respect to earth. The orientation of the spacecraft may be quite different from the simple coordinate system in which the ceiling is in the direction and the front of the craft is in a direction coplanar with the radius and the velocity. We can transform our simple coordinates to an arbitrarily oriented coordinate system through rotations. This, however, destroys the diagonal nature of the curvature matrix.Rotations are performed with a rotation matrix
such that the separation vector 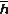is related to the separation vector before rotation by the relation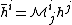.The inverse
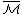of 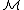is defined by,which yields
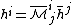.Here
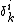is the Kronecker delta.A simple rotation matrix that rotates the coordinate axis through an angle
about the -axis is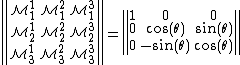.This is a rotation in the y-z plane. The inverse is obtained by switching the sign of
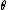.If the rotation matrix does not depend on time then the geodisic equation becomes, upon rotation
where
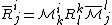.The curvature in the new coordinate system is non-diagonal. The inverse problem of transforming an arbitray coordinate system into a diagonal system can be performed mathematically with the process of diagonalization
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
.
Time dependent rotation of the local frame: Christoffel symbols
The space craft may tumble about its center of mass. In that case the rotation matrix is time dependent. If the rotation matrix is time dependent, then it does not commute with the time derivative.In that case, the rotation of the separation velocity can be written
which becomes
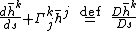
where
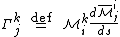
is known as a Christoffel symbol.
The geodesic equation becomes
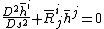,which is the same as before with the exception that the derivatives have been generalized.
Arbitrariness in the curvature
The velocity in the frame of the spacecraft can be written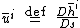.The geodesic equation becomes
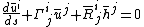..In an arbitrarily rotating spacecraft, the curvature of space is due to two terms, one due to the mass density and one due to the arbitrary rotation of the spacecraft. The arbitrary rotation is non-physical and must be eliminated in any real physical theory of gravitation. In General Relativity this is done with a process called Fermi-Walker transport
Fermi-Walker transport
Fermi-Walker transport is a process in general relativity used to define a coordinate system or reference frame such that all curvature in the frame is due to the presence of mass/energy density and not to arbitrary spin or rotation of the frame....
. In a Euclidean
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
sense, Fermi-Walker transport is simply a statement that the spacecraft is not allowed to tumble
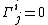
for all i and j. The only time-dependent rotations allowed are those generated by the mass density.
Geodesic equation
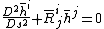
where
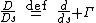
and
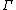is a Christoffel symbol.Field equation
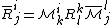
where
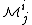is a rotation matrix and the curvature tensor is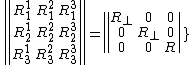.The curvature is proportional to the mass density
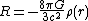.Overview of the Newtonian picture
The geodesic and field equations simply are a restatement of Newton's Law of Gravitation as seen from a local frame of reference co-moving with the mass within the local frame. This picture contains many of the elements of General Relativity, including the concept that particles travel along geodesics in a curved space (spacetime in the relativistic case) and that the curvature is due to the presence of mass density (mass/energy density in the relativistic case). This picture also contains some of the mathematical machinery of General Relativity such as tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s, Christoffel symbols, and Fermi-Walker transport
Fermi-Walker transport
Fermi-Walker transport is a process in general relativity used to define a coordinate system or reference frame such that all curvature in the frame is due to the presence of mass/energy density and not to arbitrary spin or rotation of the frame....
.
Relativistic generalization
World line
In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
s in spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
. The equations are also generalized to more complicated curvatures.
Related mathematics
- Mathematics of general relativityMathematics of general relativityThe mathematics of general relativity refers to various mathematical structures and techniques that are used in studying and formulating Albert Einstein's theory of general relativity. The main tools used in this geometrical theory of gravitation are tensor fields defined on a Lorentzian manifold...
- Basic introduction to the mathematics of curved spacetimeBasic introduction to the mathematics of curved spacetimeThe mathematics of general relativity are very complex. In Newton's theories of motions, an object's mass and length remain constant as it changes speed, and the rate of passage of time also remains unchanged. As a result, many problems in Newtonian mechanics can be solved with algebra alone...
- Tidal tensorTidal tensorIn Newton's theory of gravitation and in various relativistic classical theories of gravitation, such as general relativity, the tidal tensor represents#tidal accelerations of a cloud of test particles,...
- Frame fields in general relativityFrame fields in general relativityIn general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...