
Normal extension
Encyclopedia
In abstract algebra
, an algebraic field extension
L/K is said to be normal if L is the splitting field
of a family of polynomial
s in K[X]. Bourbaki
calls such an extension a quasi-Galois extension
.
For example,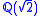 is a normal extension of
is a normal extension of  , since it is a splitting field of x2 − 2. On the other hand,
, since it is a splitting field of x2 − 2. On the other hand, 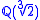 is not a normal extension of
is not a normal extension of  since the polynomial x3 − 2 has one root in it (namely,
since the polynomial x3 − 2 has one root in it (namely, 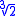 ), but not all of them (it does not have the non-real cubic roots of 2).
), but not all of them (it does not have the non-real cubic roots of 2).
The fact that is not a normal extension of
is not a normal extension of  can also be proved using the first of the two equivalent properties from above. The field
can also be proved using the first of the two equivalent properties from above. The field  of complex algebraic number
of complex algebraic number
s is an algebraic closure of containing
containing 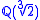 . On the other hand
. On the other hand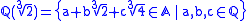
and, if ω is one of the two non-real cubic roots of 2, then the map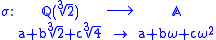
is an embedding of in
in  whose restriction to
whose restriction to  is the identity. However, σ is not an automorphism of
is the identity. However, σ is not an automorphism of 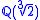 .
.
For any prime p, the extension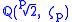 is normal of degree p(p − 1). It is a splitting field of xp − 2. Here
is normal of degree p(p − 1). It is a splitting field of xp − 2. Here 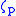 denotes any pth primitive root of unity.
denotes any pth primitive root of unity.
If L is a finite extension of K, then its normal closure is also a finite extension.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, an algebraic field extension
Algebraic extension
In abstract algebra, a field extension L/K is called algebraic if every element of L is algebraic over K, i.e. if every element of L is a root of some non-zero polynomial with coefficients in K. Field extensions that are not algebraic, i.e...
L/K is said to be normal if L is the splitting field
Splitting field
In abstract algebra, a splitting field of a polynomial with coefficients in a field is a smallest field extension of that field over which the polynomial factors into linear factors.-Definition:...
of a family of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s in K[X]. Bourbaki
Nicolas Bourbaki
Nicolas Bourbaki is the collective pseudonym under which a group of 20th-century mathematicians wrote a series of books presenting an exposition of modern advanced mathematics, beginning in 1935. With the goal of founding all of mathematics on set theory, the group strove for rigour and generality...
calls such an extension a quasi-Galois extension
Galois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
.
Equivalent properties and examples
The normality of L/K is equivalent to each of the following properties:- Let Ka be an algebraic closureAlgebraic closureIn mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of K containing L. Every embeddingEmbeddingIn mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
σ of L in Ka which restricts to the identity on K, satisfies σ(L) = L. In other words, σ is an automorphismAutomorphismIn mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of L over K. - Every irreducible polynomialIrreducible polynomialIn mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
in K[X] which has a root in L factors into linear factors in L[X]. - The minimal polynomialMinimal polynomial (field theory)In field theory, given a field extension E / F and an element α of E that is an algebraic element over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p = 0...
over K of every element in L splitsSplitting fieldIn abstract algebra, a splitting field of a polynomial with coefficients in a field is a smallest field extension of that field over which the polynomial factors into linear factors.-Definition:...
over L.
For example,
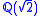 is a normal extension of
is a normal extension of  , since it is a splitting field of x2 − 2. On the other hand,
, since it is a splitting field of x2 − 2. On the other hand, 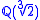 is not a normal extension of
is not a normal extension of  since the polynomial x3 − 2 has one root in it (namely,
since the polynomial x3 − 2 has one root in it (namely, 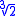 ), but not all of them (it does not have the non-real cubic roots of 2).
), but not all of them (it does not have the non-real cubic roots of 2).The fact that
 is not a normal extension of
is not a normal extension of  can also be proved using the first of the two equivalent properties from above. The field
can also be proved using the first of the two equivalent properties from above. The field  of complex algebraic number
of complex algebraic numberAlgebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s is an algebraic closure of
 containing
containing 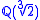 . On the other hand
. On the other hand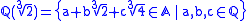
and, if ω is one of the two non-real cubic roots of 2, then the map
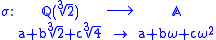
is an embedding of
 in
in  whose restriction to
whose restriction to  is the identity. However, σ is not an automorphism of
is the identity. However, σ is not an automorphism of 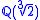 .
.For any prime p, the extension
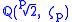 is normal of degree p(p − 1). It is a splitting field of xp − 2. Here
is normal of degree p(p − 1). It is a splitting field of xp − 2. Here 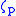 denotes any pth primitive root of unity.
denotes any pth primitive root of unity.Other properties
Let L be an extension of a field K. Then:- If L is a normal extension of K and if E is an intermediate extension (i.e., L ⊃ E ⊃ K), then L is also a normal extension of E.
- If E and F are normal extensions of K contained in L, then the compositum EF and E ∩ F are also normal extensions of K.
Normal closure
If K is a field and L is an algebraic extension of K, then there is some algebraic extension M of L such that M is a normal extension of K. Furthermore, up to isomorphism there is only one such extension which is minimal, i.e. such that the only subfield of M which contains L and which is a normal extension of K is M itself. This extension is called the normal closure of the extension L of K.If L is a finite extension of K, then its normal closure is also a finite extension.

