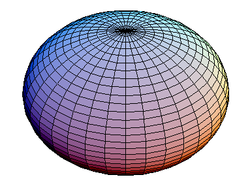
Oblate
Encyclopedia
Spheroid
A spheroid, or ellipsoid of revolution is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters....
is a rotationally symmetric
Rotational symmetry
Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
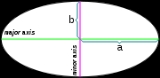
ellipsoid having a polar axis shorter than the diameter of the equatorial circle whose plane bisects it. Oblate spheroids stand in contrast to prolate spheroid
Prolate spheroid
A prolate spheroid is a spheroid in which the polar axis is greater than the equatorial diameter. Prolate spheroids stand in contrast to oblate spheroids...
s.
It can be formed by rotating an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
about its minor axis, forming an equator with the end points of the major axis. As with all ellipsoids, it can also be described by the lengths of three mutually perpendicular principal axes, which are in this case two arbitrary equatorial semi-major axes
Semi-major axis
The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
and one semi-minor axis
Semi-minor axis
In geometry, the semi-minor axis is a line segment associated with most conic sections . One end of the segment is the center of the conic section, and it is at right angles with the semi-major axis...
.
An everyday example of an oblate spheroid is the shape of the UK candy Smarties or US candy M&M's
M&M's
M&M's are dragée-like "colorful button-shaped candies" produced by Mars, Incorporated...
. The shape of the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
is very close to that of an oblate spheroid. Though local topography
Topography
Topography is the study of Earth's surface shape and features or those ofplanets, moons, and asteroids...
deviates from this idealized spheroid
Spheroid
A spheroid, or ellipsoid of revolution is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters....
, on a global scale these deviation
Deviation
Deviation may refer to:* Deviation , the difference between the value of an observation and the mean of the population in mathematics and statistics** Standard deviation, which is based on the square of the difference...
s are very small.
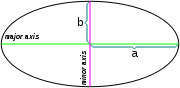
Aspect ratio
The aspect ratio of a shape is the ratio of its longer dimension to its shorter dimension. It may be applied to two characteristic dimensions of a three-dimensional shape, such as the ratio of the longest and shortest axis, or for symmetrical objects that are described by just two measurements,...
of an oblate spheroid/ellipse, b:a, is the ratio of the polar to equatorial lengths, while the flattening
Flattening
The flattening, ellipticity, or oblateness of an oblate spheroid is a measure of the "squashing" of the spheroid's pole, towards its equator...
(also called oblateness) f, is the ratio of the equatorial-polar length difference to the equatorial length:
These are just two of several different parameters used to define an ellipse and its solid body counterparts, all of which are ultimately trigonometric functions of the ellipse's modular angle, or angular eccentricity
Angular eccentricity
In the study of ellipses and related geometry, various parameters in the distortion of a circle into an ellipse are identified and employed: Aspect ratio, flattening and eccentricity....
.
The oblate spheroid is the approximate shape of many planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
s and celestial bodies
Astronomical object
Astronomical objects or celestial objects are naturally occurring physical entities, associations or structures that current science has demonstrated to exist in the observable universe. The term astronomical object is sometimes used interchangeably with astronomical body...
, including Saturn
Saturn
Saturn is the sixth planet from the Sun and the second largest planet in the Solar System, after Jupiter. Saturn is named after the Roman god Saturn, equated to the Greek Cronus , the Babylonian Ninurta and the Hindu Shani. Saturn's astronomical symbol represents the Roman god's sickle.Saturn,...
and Altair, and – to a lesser extent – the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
(with a = 6378.137 km and b ≈ 6356.752 km, providing an aspect ratio of 0.99664717, a flattening of 0.003352859934, and inverse flattening of 298.2572). It is therefore the most-used geometric figure for defining reference ellipsoid
Reference ellipsoid
In geodesy, a reference ellipsoid is a mathematically-defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body....
s, upon which cartographic and geodetic systems are based.
See also
- Aspect ratioAspect ratioThe aspect ratio of a shape is the ratio of its longer dimension to its shorter dimension. It may be applied to two characteristic dimensions of a three-dimensional shape, such as the ratio of the longest and shortest axis, or for symmetrical objects that are described by just two measurements,...
- Equatorial bulgeEquatorial bulgeAn equatorial bulge is a difference between the equatorial and polar diameters of a planet, due to the centrifugal force of its rotation. A rotating body tends to form an oblate spheroid rather than a sphere...
- EquidimensionalEquidimensionalEquidimensional is an adjective applied to objects that have nearly the same size or spread in multiple directions. As a mathematical concept, it may be applied to objects that extend across any number of dimensions...
- Figure of the EarthFigure of the EarthThe expression figure of the Earth has various meanings in geodesy according to the way it is used and the precision with which the Earth's size and shape is to be defined. The actual topographic surface is most apparent with its variety of land forms and water areas. This is, in fact, the surface...
- FlatteningFlatteningThe flattening, ellipticity, or oblateness of an oblate spheroid is a measure of the "squashing" of the spheroid's pole, towards its equator...
- LentoidLentoidLentoid is a geometric shape of a three-dimensional body, best described as a circle viewed from one direction and a convex lens viewed from an orthogonal direction...
- Oblate spheroidal coordinatesOblate spheroidal coordinatesOblate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the non-focal axis of the ellipse, i.e., the symmetry axis that separates the foci. Thus, the two foci are transformed into a ring of...
- Prolate spheroidProlate spheroidA prolate spheroid is a spheroid in which the polar axis is greater than the equatorial diameter. Prolate spheroids stand in contrast to oblate spheroids...
- Reference ellipsoidReference ellipsoidIn geodesy, a reference ellipsoid is a mathematically-defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body....


