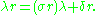Ore extension
Encyclopedia
In mathematics
, especially in the area of algebra
known as ring theory
, an Ore extension, named after Oystein Ore, is a special type of a ring extension
whose properties are relatively well understood. Ore extensions appear in several natural contexts, including skew and differential polynomial rings, group algebras of polycyclic group
s, enveloping algebras of solvable Lie algebras, and coordinate rings of quantum group
s.
, σ:R → R is an injective
ring homomorphism
, and δ:R → R is a σ-derivation of R, which means that δ is a homomorphism of abelian group
s satisfying
Then the Ore extension R[λ;σ,δ] is the ring obtained by giving the ring of polynomials
R[λ] a new multiplication, subject to the identity
If δ = 0 (i.e., is the zero map) then the Ore extension is denoted R[λ; σ] and is called a skew polynomial ring. If σ = 1 (i.e., the identity map) then the Ore extension is denoted R[λ,δ] and is called a differential polynomial ring.
, σ the identity ring endomorphism, and δ the polynomial derivative.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the area of algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
known as ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, an Ore extension, named after Oystein Ore, is a special type of a ring extension
Ring extension
In mathematics, more specifically in ring theory, a ring extension or extension ring is a ring R with a subring S. We write R/S and say R is a ring extension of S...
whose properties are relatively well understood. Ore extensions appear in several natural contexts, including skew and differential polynomial rings, group algebras of polycyclic group
Polycyclic group
In mathematics, a polycyclic group is a solvable group that satisfies the maximal condition on subgroups...
s, enveloping algebras of solvable Lie algebras, and coordinate rings of quantum group
Quantum group
In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
s.
Definition
Suppose that R is a ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, σ:R → R is an injective
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
ring homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
, and δ:R → R is a σ-derivation of R, which means that δ is a homomorphism of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s satisfying
Then the Ore extension R[λ;σ,δ] is the ring obtained by giving the ring of polynomials
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
R[λ] a new multiplication, subject to the identity
If δ = 0 (i.e., is the zero map) then the Ore extension is denoted R[λ; σ] and is called a skew polynomial ring. If σ = 1 (i.e., the identity map) then the Ore extension is denoted R[λ,δ] and is called a differential polynomial ring.
Examples
The Weyl algebras are Ore extensions, with R any a commutative polynomial ringPolynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
, σ the identity ring endomorphism, and δ the polynomial derivative.
Properties
- An Ore extension of a domainDomain (ring theory)In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
is a domain. - If σ is an automorphismAutomorphismIn mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
and R is a left Noetherian ringNoetherian ringIn mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
then the Ore extension R[λ;σ,δ] is also left Noetherian.