
Out(Fn)
Encyclopedia
In mathematics
, Out(Fn) is the outer automorphism group
of a free group
on n generator
s. These groups play an important role in geometric group theory
.
on a cell complex known as Culler
–Vogtmann
Outer space, which can be thought of as the Teichmüller space
for a bouquet of circles
.
class of a homotopy equivalence from X to the Bouquet of n circles. An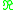 - Graph is just a weighted Graph
- Graph is just a weighted Graph
with weights in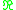 . The sum of all weights should be 1 and all weights should be positive. To avoid ambiguity (and to get a finite dimensional space) it is furthermore required, that the valency of each vertex should be at least 2.
. The sum of all weights should be 1 and all weights should be positive. To avoid ambiguity (and to get a finite dimensional space) it is furthermore required, that the valency of each vertex should be at least 2.
A more descriptive view avoiding the homotopy equivalence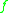 is the following. We may fix an identification of the fundamental group
is the following. We may fix an identification of the fundamental group
of the bouquet of n circles with the free group
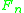 in
in  variables. Furthermore we may choose a maximal tree
variables. Furthermore we may choose a maximal tree
in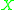 and choose for each remaining edge a direction. We will now assign to each remaining edge
and choose for each remaining edge a direction. We will now assign to each remaining edge  a word in
a word in  in the following way. Consider the closed path starting with
in the following way. Consider the closed path starting with  and then going back to the origin of
and then going back to the origin of  in the maximal tree. Composing this path with
in the maximal tree. Composing this path with  we get a closed path in a bouquet of
we get a closed path in a bouquet of  circles and hence a element in its fundamental group
circles and hence a element in its fundamental group 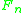 . This element is not well defined; if we change f by a free homotopy we obtain another element. It turns out, that those two elements are conjugate to each other, and hence we can choose the unique cyclically reduced element in this conjugacy class.
. This element is not well defined; if we change f by a free homotopy we obtain another element. It turns out, that those two elements are conjugate to each other, and hence we can choose the unique cyclically reduced element in this conjugacy class.
It is possible to reconstruct the free homotopy type of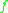 from these data. This view has the advantage, that it avoids the extra choice of
from these data. This view has the advantage, that it avoids the extra choice of 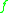 and has the disadvantage that additional ambiguity arises, because one has to choose a maximal tree and a orientation of the remaining edges.
and has the disadvantage that additional ambiguity arises, because one has to choose a maximal tree and a orientation of the remaining edges.
The operation of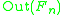 on the outer space is defined as follows. Every Automorphism
on the outer space is defined as follows. Every Automorphism 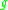 of
of 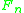 induces a self homotopy equivalence
induces a self homotopy equivalence 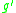 of the bouquet of
of the bouquet of  circles. Composing
circles. Composing  with
with 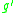 gives the desired action. And in the other model it is just application of
gives the desired action. And in the other model it is just application of 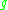 and making the resulting word cyclically reduced.
and making the resulting word cyclically reduced.
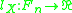 . A word in
. A word in 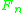 determines via the chosen homotopy equivalence a closed path in
determines via the chosen homotopy equivalence a closed path in 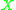 . The length of the word is then the minimal length of a path in the free homotopy class of that closed path. Such a length function is constant on each conjugacy class. The assignment
. The length of the word is then the minimal length of a path in the free homotopy class of that closed path. Such a length function is constant on each conjugacy class. The assignment 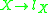 defines an embedding of the outer space to some infinite dimensional projective space.
defines an embedding of the outer space to some infinite dimensional projective space.
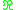 -graphs, which have combinatorically the same underlying graph and the same edges are labeled with the same words (only the length of the edges may differ). The boundary simplices of such a simplex consists of all graphs, that arise from this graph by collapsing a edge. If that edge is a loop it cannot be collapsed without changing the homotopy type of the graph. Hence there is no boundary simplex. So one can think about the outer space as a simplicial complex with some simplices removed. It is easy to verify, that the action of
-graphs, which have combinatorically the same underlying graph and the same edges are labeled with the same words (only the length of the edges may differ). The boundary simplices of such a simplex consists of all graphs, that arise from this graph by collapsing a edge. If that edge is a loop it cannot be collapsed without changing the homotopy type of the graph. Hence there is no boundary simplex. So one can think about the outer space as a simplicial complex with some simplices removed. It is easy to verify, that the action of 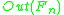 is simplicial and has finite isotropy groups.
is simplicial and has finite isotropy groups.
Out(Fn) → GL(n,Z)
, the latter being the automorphism group of Zn. This map is onto, making Out(Fn) a group extension
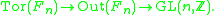
The kernel Tor(Fn) is the Torelli group of Fn.
In the case n = 2, the map Out(F2) → GL(2,Z) is an isomorphism
.
of a bouquet of circles
, Out(Fn) can be thought of as the mapping class group
of a bouquet of n circles. (The mapping class group of a surface is the outer automorphism group of the fundamental group of that surface.) By analogy, Out(Fn) can be described as the quotient
G/H, where G is the group of all self-homotopy equivalences of the bouquet of circles, and H is the subgroup of G consisting of homotopy equivalences that are homotopic
to the identity map
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Out(Fn) is the outer automorphism group
Outer automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
of a free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
on n generator
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
s. These groups play an important role in geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
.
Outer space
Out(Fn) acts geometricallyGeometric group action
In mathematics, specifically geometric group theory, a geometric group action is a certain type of action of a discrete group on a metric space.-Definition:In geometric group theory, a geometry is any proper, geodesic metric space...
on a cell complex known as Culler
Marc Culler
Marc Edward Culler is an American mathematician who works in geometric group theory and low-dimensional topology. A native Californian, Culler did his undergraduate work at the University of California at Santa Barbara and his graduate work at Berkeley where he graduated in 1978. He is now at the...
–Vogtmann
Karen Vogtmann
Karen Vogtmann is a U.S. mathematician working primarily in the area of geometric group theory. She is known for having introduced, in a 1986 paper with Marc Culler, an object now known as the Culler–Vogtmann Outer space...
Outer space, which can be thought of as the Teichmüller space
Teichmüller space
In mathematics, the Teichmüller space TX of a topological surface X, is a space that parameterizes complex structures on X up to the action of homeomorphisms that are isotopic to the identity homeomorphism...
for a bouquet of circles
Bouquet of circles
In mathematics, a rose is a topological space obtained by gluing together a collection of circles along a single point. The circles of the rose are called petals. Roses are important in algebraic topology, where they are closely related to free groups.- Definition :A rose is a wedge sum of circles...
.
Definition
A point of the outer space is essentially an R-graph X homotopy equivalent to a bouquet of n circles together with a certain choice of a free homotopyHomotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
class of a homotopy equivalence from X to the Bouquet of n circles. An
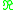 - Graph is just a weighted Graph
- Graph is just a weighted GraphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
with weights in
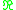 . The sum of all weights should be 1 and all weights should be positive. To avoid ambiguity (and to get a finite dimensional space) it is furthermore required, that the valency of each vertex should be at least 2.
. The sum of all weights should be 1 and all weights should be positive. To avoid ambiguity (and to get a finite dimensional space) it is furthermore required, that the valency of each vertex should be at least 2.A more descriptive view avoiding the homotopy equivalence
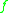 is the following. We may fix an identification of the fundamental group
is the following. We may fix an identification of the fundamental groupFundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the bouquet of n circles with the free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
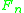 in
in  variables. Furthermore we may choose a maximal tree
variables. Furthermore we may choose a maximal treeSpanning tree (mathematics)
In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
in
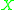 and choose for each remaining edge a direction. We will now assign to each remaining edge
and choose for each remaining edge a direction. We will now assign to each remaining edge  a word in
a word in  in the following way. Consider the closed path starting with
in the following way. Consider the closed path starting with  and then going back to the origin of
and then going back to the origin of  in the maximal tree. Composing this path with
in the maximal tree. Composing this path with  we get a closed path in a bouquet of
we get a closed path in a bouquet of  circles and hence a element in its fundamental group
circles and hence a element in its fundamental group 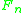 . This element is not well defined; if we change f by a free homotopy we obtain another element. It turns out, that those two elements are conjugate to each other, and hence we can choose the unique cyclically reduced element in this conjugacy class.
. This element is not well defined; if we change f by a free homotopy we obtain another element. It turns out, that those two elements are conjugate to each other, and hence we can choose the unique cyclically reduced element in this conjugacy class.It is possible to reconstruct the free homotopy type of
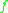 from these data. This view has the advantage, that it avoids the extra choice of
from these data. This view has the advantage, that it avoids the extra choice of 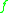 and has the disadvantage that additional ambiguity arises, because one has to choose a maximal tree and a orientation of the remaining edges.
and has the disadvantage that additional ambiguity arises, because one has to choose a maximal tree and a orientation of the remaining edges.The operation of
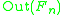 on the outer space is defined as follows. Every Automorphism
on the outer space is defined as follows. Every Automorphism 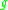 of
of 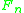 induces a self homotopy equivalence
induces a self homotopy equivalence 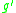 of the bouquet of
of the bouquet of  circles. Composing
circles. Composing  with
with 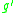 gives the desired action. And in the other model it is just application of
gives the desired action. And in the other model it is just application of 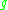 and making the resulting word cyclically reduced.
and making the resulting word cyclically reduced.Connection to length functions
Every point in the outer space determines a unique length function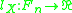 . A word in
. A word in 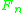 determines via the chosen homotopy equivalence a closed path in
determines via the chosen homotopy equivalence a closed path in 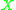 . The length of the word is then the minimal length of a path in the free homotopy class of that closed path. Such a length function is constant on each conjugacy class. The assignment
. The length of the word is then the minimal length of a path in the free homotopy class of that closed path. Such a length function is constant on each conjugacy class. The assignment 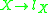 defines an embedding of the outer space to some infinite dimensional projective space.
defines an embedding of the outer space to some infinite dimensional projective space.Simplicial structure on the outer space
In the second model a open simplex is given by all those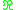 -graphs, which have combinatorically the same underlying graph and the same edges are labeled with the same words (only the length of the edges may differ). The boundary simplices of such a simplex consists of all graphs, that arise from this graph by collapsing a edge. If that edge is a loop it cannot be collapsed without changing the homotopy type of the graph. Hence there is no boundary simplex. So one can think about the outer space as a simplicial complex with some simplices removed. It is easy to verify, that the action of
-graphs, which have combinatorically the same underlying graph and the same edges are labeled with the same words (only the length of the edges may differ). The boundary simplices of such a simplex consists of all graphs, that arise from this graph by collapsing a edge. If that edge is a loop it cannot be collapsed without changing the homotopy type of the graph. Hence there is no boundary simplex. So one can think about the outer space as a simplicial complex with some simplices removed. It is easy to verify, that the action of 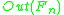 is simplicial and has finite isotropy groups.
is simplicial and has finite isotropy groups.Structure
The abelianization map Fn → Zn induces a homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
Out(Fn) → GL(n,Z)
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
, the latter being the automorphism group of Zn. This map is onto, making Out(Fn) a group extension
Group extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence...
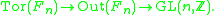
The kernel Tor(Fn) is the Torelli group of Fn.
In the case n = 2, the map Out(F2) → GL(2,Z) is an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
.
Analogy with mapping class groups
Because Fn is the fundamental groupFundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of a bouquet of circles
Bouquet of circles
In mathematics, a rose is a topological space obtained by gluing together a collection of circles along a single point. The circles of the rose are called petals. Roses are important in algebraic topology, where they are closely related to free groups.- Definition :A rose is a wedge sum of circles...
, Out(Fn) can be thought of as the mapping class group
Mapping class group
In mathematics, in the sub-field of geometric topology, the mapping class groupis an important algebraic invariant of a topological space. Briefly, the mapping class group is a discrete group of 'symmetries' of the space.-Motivation:...
of a bouquet of n circles. (The mapping class group of a surface is the outer automorphism group of the fundamental group of that surface.) By analogy, Out(Fn) can be described as the quotient
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
G/H, where G is the group of all self-homotopy equivalences of the bouquet of circles, and H is the subgroup of G consisting of homotopy equivalences that are homotopic
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
to the identity map
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
.

