PRO (category theory)
Encyclopedia
In category theory
, a PRO is a strict monoidal category
whose objects are the natural numbers (incl. zero), and whose tensor product is given on objects by the addition on numbers.
Some examples of PROs:
The name PRO is an abbreviation of "PROduct category". PROBs and PROPs are defined similarly with the additional requirement for the category to be braided, and to have a symmetry (that is, a permutation), respectively.
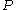in a monoidal category
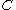is a strict monoidal functor
from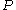
to 
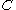. Every PRO 
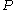and category 
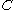give rise to a category 
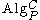of algebras whose objects are the algebras of 
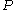in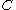 
and whose morphisms are the natural transformations between them.
For example:
More precisely, what we mean here by "the algebras of
in 
are the monoid objects in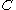 
" for example is that the category of algebras of 
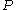in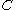 
is equivalent
to the category of monoids in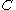
.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a PRO is a strict monoidal category
Monoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
whose objects are the natural numbers (incl. zero), and whose tensor product is given on objects by the addition on numbers.
Some examples of PROs:
- the discrete category
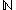of natural numbers, - the category FinSetFinSetIn the mathematical field of category theory, FinSet is the category whose objects are all finite sets and whose morphisms are all functions between them...
of natural numbers and functions between them, - the category Bij of natural numbers and bijections,
- the category Inj of natural numbers and injections,
- the simplicial categorySimplicial categoryIn mathematics, the simplex category is the category of finite ordinals and order preserving maps. It is used to define simplicial and cosimplicial objects.-Formal definition:...
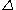of natural numbers and monotonic functionMonotonic functionIn mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
s.
The name PRO is an abbreviation of "PROduct category". PROBs and PROPs are defined similarly with the additional requirement for the category to be braided, and to have a symmetry (that is, a permutation), respectively.
Algebras of a PRO
An algebra of a PRO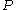 in a monoidal categoryMonoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
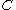is a strict monoidal functorMonoidal functor
In category theory, monoidal functors are functors between monoidal categories which preserve the monoidal structure. More specifically, a monoidal functor between two monoidal categories consists of a functor between the categories, along with two coherence maps—a natural transformation and a...
from
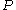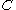to . Every PRO 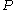and category 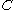give rise to a category 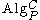of algebras whose objects are the algebras of 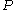in 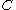and whose morphisms are the natural transformations between them.For example:
- an algebra of
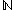is just an object of 
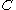, - an algebra of FinSet is a commutative monoid object of
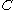, - an algebra of
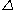is a monoid object in 
.
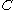More precisely, what we mean here by "the algebras of
in are the monoid objects in 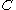" for example is that the category of algebras of 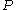in 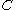is equivalentEquivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
to the category of monoids in
.
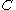