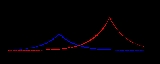
Peakon
Encyclopedia
In the theory of integrable system
s, a peakon ("peaked soliton") is a soliton
with discontinuous first derivative
; the wave profile is shaped like the graph of the function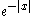
. Some examples of non-linear partial differential equations with (multi-)peakon solutions are the Camassa–Holm shallow water wave equation and the Degasperis–Procesi equation.
Since peakon solutions are only piecewise differentiable, they must be interpreted in a suitable weak sense
.
The concept was introduced in 1993 by Camassa and Holm in the short but much cited paper where they derived their shallow water equation.
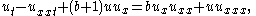
where
is the unknown function, and b is a parameter.
In terms of the auxiliary function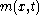
defined by the relation 
, the equation takes the simpler form
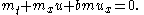
This equation is integrable
for exactly two values of b, namely b = 2 (the Camassa–Holm equation) and b = 3 (the Degasperis–Procesi equation).
,
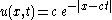which is a peaked solitary wave with amplitude c and speed c.
This solution is called a (single) peakon solution,
or simply a peakon.
If c is negative, the wave moves to the left with the peak pointing downwards,
and then it is sometimes called an antipeakon.
It is not immediately obvious in what sense the peakon solution satisfies the PDE.
Since the derivative ux has a jump discontinuity at the peak,
the second derivative uxx must be taken in the sense of distributions
and will contain a Dirac delta function
;
in fact,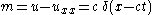
.
Now the product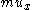
occurring in the PDE seems to be undefined, since the distribution m is supported at the very point where the derivative ux is undefined. An ad hoc
interpretation is to take the value of ux at that point to equal the average of its left and right limits (zero, in this case). A more satisfactory way to make sense of the solution is to invert the relationship between u and m by writing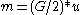
, where 
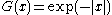, and use this to rewrite the PDE as a (nonlocal) hyperbolic conservation law:
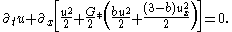
(The star denotes convolution
with respect to x.)
In this formulation the function u can simply be interpreted as a weak solution
in the usual sense.
Multipeakon solutions are formed by taking a linear combination of several peakons, each with its own time-dependent amplitude and position. (This is a very simple structure compared to the multisoliton solutions of most other integrable PDEs, like the Korteweg–de Vries equation
for instance.)
The n-peakon solution thus takes the form
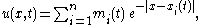
where the 2n functions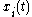
and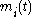 
must be chosen suitably in order for u to satisfy the PDE.
For the "b-family" above it turns out that this ansatz indeed gives a solution, provided that the system of ODEs
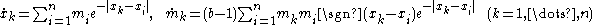
is satisfied. (Here sgn denotes the sign function
.)
Note that the right-hand side of the equation for
is obtained by substituting 
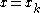in the formula for u.
Similarly, the equation for
can be expressed in terms of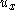 
, if one interprets the derivative of 
at x = 0 as being zero.
This gives the following convenient shorthand notation for the system:
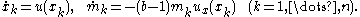
The first equation provides some useful intuition about peakon dynamics: the velocity of each peakon equals the elevation of the wave at that point.
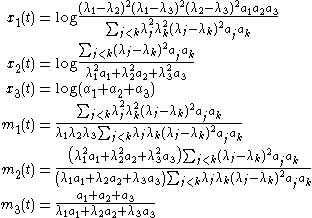
where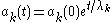
, and where the 2n constants 
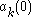and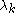 
are determined from initial conditions. The general solution for arbitrary n can be expressed in terms of symmetric function
s of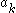
and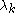 
. The general n-peakon solution in the Degasperis–Procesi case b = 3 is similar in flavour, although the detailed structure is more complicated.
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
s, a peakon ("peaked soliton") is a soliton
Soliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
with discontinuous first derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
; the wave profile is shaped like the graph of the function
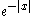. Some examples of non-linear partial differential equations with (multi-)peakon solutions are the Camassa–Holm shallow water wave equation and the Degasperis–Procesi equation.Since peakon solutions are only piecewise differentiable, they must be interpreted in a suitable weak sense
Weak solution
In mathematics, a weak solution to an ordinary or partial differential equation is a function for which the derivatives may not all exist but which is nonetheless deemed to satisfy the equation in some precisely defined sense. There are many different definitions of weak solution, appropriate for...
.
The concept was introduced in 1993 by Camassa and Holm in the short but much cited paper where they derived their shallow water equation.
A family of equations with peakon solutions
The primary example of a PDE which supports peakon solutions is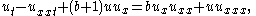where
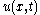is the unknown function, and b is a parameter.In terms of the auxiliary function
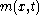defined by the relation , the equation takes the simpler form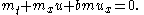This equation is integrable
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
for exactly two values of b, namely b = 2 (the Camassa–Holm equation) and b = 3 (the Degasperis–Procesi equation).
The single peakon solution
The PDE above admits the travelling wave solution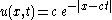,which is a peaked solitary wave with amplitude c and speed c.
This solution is called a (single) peakon solution,
or simply a peakon.
If c is negative, the wave moves to the left with the peak pointing downwards,
and then it is sometimes called an antipeakon.
It is not immediately obvious in what sense the peakon solution satisfies the PDE.
Since the derivative ux has a jump discontinuity at the peak,
the second derivative uxx must be taken in the sense of distributions
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
and will contain a Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
;
in fact,
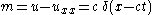.Now the product
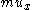occurring in the PDE seems to be undefined, since the distribution m is supported at the very point where the derivative ux is undefined. An ad hocAd hoc
Ad hoc is a Latin phrase meaning "for this". It generally signifies a solution designed for a specific problem or task, non-generalizable, and not intended to be able to be adapted to other purposes. Compare A priori....
interpretation is to take the value of ux at that point to equal the average of its left and right limits (zero, in this case). A more satisfactory way to make sense of the solution is to invert the relationship between u and m by writing
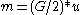, where 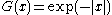, and use this to rewrite the PDE as a (nonlocal) hyperbolic conservation law: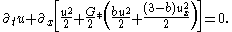(The star denotes convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
with respect to x.)
In this formulation the function u can simply be interpreted as a weak solution
Weak solution
In mathematics, a weak solution to an ordinary or partial differential equation is a function for which the derivatives may not all exist but which is nonetheless deemed to satisfy the equation in some precisely defined sense. There are many different definitions of weak solution, appropriate for...
in the usual sense.
Multipeakon solutions
Korteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
for instance.)
The n-peakon solution thus takes the form
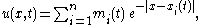
where the 2n functions
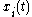and 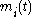must be chosen suitably in order for u to satisfy the PDE.
For the "b-family" above it turns out that this ansatz indeed gives a solution, provided that the system of ODEs
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
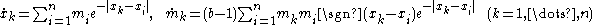
is satisfied. (Here sgn denotes the sign function
Sign function
In mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function ....
.)
Note that the right-hand side of the equation for
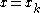is obtained by substituting in the formula for u.Similarly, the equation for
can be expressed in terms of 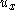, if one interprets the derivative of at x = 0 as being zero.This gives the following convenient shorthand notation for the system:
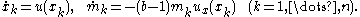
The first equation provides some useful intuition about peakon dynamics: the velocity of each peakon equals the elevation of the wave at that point.
Explicit solution formulas
In the integrable cases b = 2 and b = 3, the system of ODEs describing the peakon dynamics can be solved explicitly for arbitrary n in terms of elementary functions, using inverse spectral techniques. For example, the solution for n = 3 in the Camassa–Holm case b = 2 is given by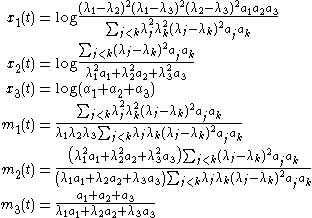where
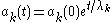, and where the 2n constants 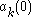and 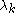are determined from initial conditions. The general solution for arbitrary n can be expressed in terms of symmetric functionSymmetric function
In algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
s of
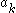and 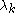. The general n-peakon solution in the Degasperis–Procesi case b = 3 is similar in flavour, although the detailed structure is more complicated.