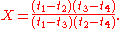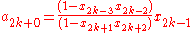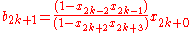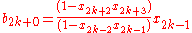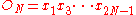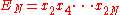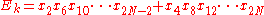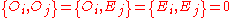Pentagram map
Encyclopedia
In mathematics
, the pentagram map is a discrete dynamical system
on the moduli space
of polygons in the projective plane
. The pentagram
map takes a given polygon, finds the intersections of the shortest diagonals of the polygon, and constructs a new polygon from these intersections.
Richard Schwartz
introduced the pentagram map for a general polygon in a 1992 paper
though it seems that the special case, in which
the map is defined for pentagons only, goes back at
least to a 1945 paper of Theodore Motzkin
.
The pentagram map is similar in spirit to the constructions underlying Desargues' Theorem
and Poncelet's porism
. It echoes the rationale and construction underlying a conjecture of Branko Grünbaum
concerning
the diagonals of a polygon.
of the polygon
P are given by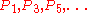 The image of P under the pentagram map is the
The image of P under the pentagram map is the
polygon Q with vertices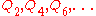 as shown in the figure. Here
as shown in the figure. Here 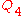 is the intersection of the diagonals
is the intersection of the diagonals
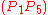 and
and 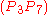 , and so on.
, and so on.
On a basic level, one can think of the pentagram map as an operation defined on convex
polygons in the plane. From a more
sophisticated point of view,
the pentagram map is defined for a polygon contained in the projective plane
over a field
provided that
the vertices
are in sufficiently general position
.
The pentagram map commutes with projective transformations and thereby induces a mapping
on the
moduli space
of projective equivalence classes of polygons.
 is slightly problematic, in the sense that the
is slightly problematic, in the sense that the
indices of the P-vertices are naturally odd integers whereas the indices of
Q-vertices are naturally even
integers. A more conventional approach to the labeling would be to label the
vertices of P and Q by integers of the same parity. One can arrange this
either by adding or subtracting 1 from each of the indices of the Q-vertices.
Either choice is equally canonical. An even more conventional choice
would be to label the vertices of P and Q by consecutive integers, but
again there are 2 natural choices for how to align these labellings:
Either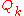 is just clockwise from
is just clockwise from 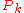
or just counterclockwise. In most papers on the subject, some choice
is made once and for all at the beginning of the paper and then the
formulas are tuned to that choice.
There is a perfectly natural way to label the vertices of the
second iterate of the pentagram map by consecutive integers. For
this reason, the second iterate of the pentagram map is more
naturally considered as an iteration defined on labeled polygons.
See the figure.
twisted polygons.
A twisted N-gon is a bi-infinite sequence of
points in the projective plane that is N-periodic modulo a projective transformation
That is, some projective transformation M carries
 to
to  for all k.
for all k.
The map M is called the monodromy
of the twisted N-gon.
When M is the identity, a twisted N-gon can be interpreted
as an ordinary N-gon whose vertices have been listed
out repeatedly. Thus, a twisted N-gon is a generalization
of an ordinary N-gon.
Two twisted N-gons are equivalent if a projective transformation
carries one to the other. The moduli space of
twisted N-gons is the set of equivalence classes of
twisted N-gons. The space of twisted N-gons contains
the space of ordinary N-gons as a sub-variety of
co-dimension 8.
s.
This is to say that there is always a projective transformation carrying a
pentagon to its image under the pentagram map. It
is very likely that this (easy) result was known to the 19th century projective geometers.
Indeed, one can deduce this result from a theorem
of Darboux
concerning Poncelet
polygons
The map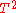 is the identity on the space of labeled
is the identity on the space of labeled
hexagons.
Here T is the second iterate of the pentagram map, which
acts naturally on labeled hexagons, as described above. This
is to say that the hexagons and
and
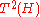 are equivalent by a label-preserving
are equivalent by a label-preserving
projective transformation. More precisely, the
hexagons and
and 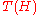 are
are
projectively equivalent, where is the labeled
is the labeled
hexagon obtained from by shifting the labels by 3.
by shifting the labels by 3.
See the figure.
It seems entirely possible that this fact was also known
in the 19th century.
The action of the pentagram map on pentagons and hexagons is similar in spirit to
classical configuration theorems in projective geometry such as Pascal's theorem
,
Desargues's theorem and others.
polygon
exponentially fast to a point.
This is to say that the diameter of
the nth iterate of a convex polygon is less than
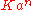
for constants and
and
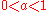 which depend
which depend
on the initial polygon.
Here we are taking about the geometric
action on the polygons themselves, not on the moduli
space of projective equivalence classes of polygons.
The context for the pentagram map is projective geometry
.
Projective geometry is the geometry of our vision. When one looks at the top of a glass,
which is a circle
, one typically sees an ellipse
. When one looks at a rectangular
door, one sees a typically non-rectangular quadrilateral
. Projective transformations convert between the
various shapes one can see when looking at same object from different points of view. This is why it
plays such an important role in old topics like perspective drawing and new ones like computer vision
.
Projective geometry is built around the fact that a straight line
looks
like a straight line from any perspective. The straight lines are the building blocks for the subject.
The pentagram map is defined entirely in terms of points and straight lines.
This makes it adapted to projective geometry. If you look at the pentagram
map from another point of view (i.e., you tilt the paper on which it is drawn) then
you are still looking at the pentagram map. This explains the statement that the
pentagram map commutes with projective transformations.
The pentagram map is fruitfully considered as a mapping
on the
moduli space of polygons.
A moduli space
is an auxiliary space whose points index other objects.
For example, in Euclidean geometry
, the sum of the angles of a triangle
is
always 180 degrees. You can specify a triangle
(up to scale) by giving
3 positive numbers, such that
such that 
So, each point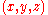 , satisfying the constraints just mentioned,
, satisfying the constraints just mentioned,
indexes a triangle (up to scale). One might say that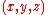 are
are
coordinates for the moduli space of scale equivalence classes of triangles.
If you want to index all possible quadrilaterals, either up to scale or not, you
would need some additional parameters. This would lead to a higher dimension
al
moduli space. The moduli space relevant to the pentagram map
is the moduli space of projective equivalence classes of polygons. Each point
in this space corresponds to a polygon, except that two polygons which are
different views of each other are considered the same. Since the pentagram
map is adapted to projective geometry, as mentioned above, it induces a
mapping
on this particular moduli space. That is, given any point
in the moduli space, you can apply the pentagram map to the corresponding
polygon and see what new point you get.
The reason for considering what the pentagram map does to the moduli
space is that it gives more salient features of the map. If you just watch,
geometrically, what happens to an individual polygon, say a convex
polygon, then repeated application shrinks the polygon to a point.
To see things more clearly, you might dilate the shrinking family of
polygons so that they all have, say, the same area
. If you do this,
then typically you will see that the family of polygons gets long and
thin. Now you can change the aspect ratio
so as to try to get yet a better view of these polygons. If you do this
process as systematically as possible, you find that you are simply
looking at what happens to points in the moduli space. The attempts
to zoom in to the picture in the most perceptive possible way lead
to the introduction of the moduli space.
To explain how the pentagram map acts on the moduli space, one must say a few words about the torus
.
One way to roughly define the torus is to say that it is the surface of an idealized donut
.
Another way is that it is the playing field for the Asteroids video game.
yet another way to describe the torus is to say that it is a computer screen with wrap, both left-to-right
and up-to-down.
The torus
is a classical example of what is known in mathematics as a manifold
.
This is a space that looks kind of like ordinary Euclidean space
at each point, but
somehow is hooked together differently. A sphere
is another example of a manifold.
This is why it took people so long to figure out that the Earth
was not flat; on
small scales one cannot easily distinguish a sphere from a plane
. So, too, with
manifolds like the torus. There are higher dimensional tori as well.
You could imagine playing Asteroids in your room, where you can freely go through
the walls and ceiling/floor, popping out on the opposite side.
One can do experiments with the pentagram map, where one looks at how
this mapping acts on the moduli space of polygons. One starts with a point
and just traces what happens to it as the map is applied over and over
again. One sees a surprising thing: These points seem to line up along
multi-dimensional tori. These invisible tori fill
up the moduli space sort of like the way
the layers of an onion fill up the onion itself, or how the
individual cards in a deck fill up the deck. The technical statement
is that the tori make a foliation
of the moduli space. The
tori have half the dimension of the moduli space. For instance,
the moduli space of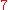 -gons is
-gons is 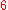 dimensional and the
dimensional and the
tori in this case are dimensional.
dimensional.
The tori are invisible subsets of the moduli space. They are
only revealed when one does the pentagram map and watches a point
move round and round, filling up one of the tori.
Roughly speaking, when dynamical systems have these invariant
tori, they are called integrable systems.
Most of the results in this article have to
do with establishing that the pentagram map is an integrable system, that
these tori really exist.
The monodromy invariants, discussed
below, turn out to be the equations for the tori. The Poisson bracket, discussed below,
is a more sophisticated math gadget that sort of encodes the local geometry
of the tori. What is nice is that the various objects fit together exactly, and
together add up to a proof that this torus motion really exists.
. Any finite list of points in the projective line can be moved into the affine
line by a suitable projective transformation.
Given the four points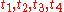 in the affine line one
in the affine line one
defines the (inverse) cross ratio
Most authors consider 1/X to be the cross-ratio
, and that is why X is called the inverse cross ratio. The inverse cross ratio is invariant under projective transformations and thus makes sense for points in the projective line. However,
the formula above only makes sense for points in the affine line.
In the slightly more general set-up below, the cross ratio makes sense
for any four collinear points in projective space
One just identifies the
line containing the points with the projective line by a suitable projective transformation and then uses the formula above.
The result is independent of any choices made in the identification.
The inverse cross ratio is used in order to define a coordinate system on the moduli space
of polygons, both ordinary and twisted.
Suppose that P is a polygon
. A flag of P is a pair (p,L), where p is a vertex of P and L is an adjacent line of P.
Each vertex of P is involved in 2 flags, and likewise each edge of P is involved in 2 flags.
The flags of P are ordered according to the orientation of P, as shown in the figure.
In this figure, a flag is represented by a thick arrow. Thus, there are 2N flags associated
to an N-gon.
Let P be an N-gon, with flags
To each flag F, we associate the inverse cross ratio of the points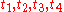 shown in the figure
shown in the figure
at left.
In this way, one associates numbers to an n-gon. If two n-gons are
to an n-gon. If two n-gons are
related by a projective transformation, they get the same coordinates. Sometimes the
variables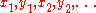 are used in place of
are used in place of
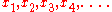
The corner invariants make sense on the moduli space of twisted polygons.
When one defines the corner invariants of a twisted polygon, one obtains
a 2N-periodic bi-infinite sequence of numbers. Taking one period
of this sequence identifies a twisted N-gon with a point
in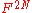 where F is the underlying field.
where F is the underlying field.
Conversely, given almost any (in the sense of measure theory) point in
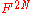 one can construct a twisted N-gon having
one can construct a twisted N-gon having
this list of corner invariants. Such a list will not always give rise
to an ordinary polygon; there are an additional 8 equations which
the list must satisfy for it to give rise to an ordinary N-gon.
developed by Sergei Tabachnikov and Valentin Ovsienko.
One describes a polygon in the projective plane
by a sequence of vectors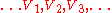 in
in
 so that each consecutive triple of vectors
so that each consecutive triple of vectors
spans a parallelopiped having unit volume. This leads to the
relation
The coordinates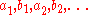
serve as coordinates for the moduli space of twisted
N-gons as long as N is not divisible by 3.
The (ab) coordinates bring out the close analogy between twisted polygons
and solutions of 3rd order linear ordinary differential equations, normalized
to have unit Wronskian
.
corner coordinates. The
equations work more gracefully when one considers the second
iterate of the pentagram map, thanks to the
canonical labelling scheme discussed above. The second iterate of the
pentagram map is the composition
 .
.
The maps and
and  are birational mappings
are birational mappings
of order 2, and have the following action.
where
(Note: the index 2k+0 is just 2k. The 0 is added to align the formulas.)
In these coordinates, the pentagram map is a birational mapping of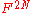
a certain compatibility rule for labelings on the edges of triangular grid,
as shown in the figure. In this interpretation, the corner invariants of a polygon
P label the non-horizontal edges of a single row, and then the non-horizontal
edges of subsequent rows are labeled by the corner invariants of
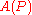 ,
,
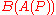 ,
,
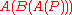 ,
,
and so forth. the compatibility rules are
These rules are meant to hold for all configurations which are
congruent
to the ones shown in the figure.
In other words, the figures involved in the relations can be
in all possible positions and orientations.
The labels on the horizontal edges are simply
auxiliary variables introduced to make the formulas simpler.
Once a single row of non-horizontal edges is provided,
the remaining rows are uniquely determined by the
compatibility rules.
that the two quantities
are invariant under the pentagram map.
This observation is closely related to the 1991 paper of Joseph Zaks
concerning the diagonals of a polygon.
When N = 2k is even, the functions
are likewise seen, directly from the formula, to be invariant
functions. All these products turn out
to be Casimir invariant
s with respect to the invariant
Poisson bracket discussed below. At the same time,
the functions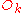 and
and  are
are
the simplest examples of the monodromy invariants defined below.
The level sets of the function
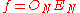 are compact
are compact
, when f is restricted to
the moduli space of real convex
polygons.
Hence, each orbit
of the pentagram map acting on this space has a compact
closure
.
convex
polygon
s, has an invariant volume form
.
At the same time, as was already mentioned, the function has
has
compact
level sets on X. These two properties combine with the
Poincare recurrence theorem
to imply that the action of the
pentagram map on X is recurrent: The orbit of almost any equivalence class
of convex polygon P returns infinitely often to every neighborhood of P.
This is to say that, modulo projective transformations, one typically
sees nearly the same shape, over and over again, as one iterates
the pentagram map.
(It is important to remember that one is considering the projective
equivalence classes of convex polygons. The fact that the pentagram map
visibly shrinks a convex polygon is irrelevant.)
It is worth mentioning that the recurrence result is
subsumed by the complete integrability results discussed below.
on the moduli space
that are invariant under the pentagram map.
With a view towards defining the monodromy invariants,
say that a block is either a single integer
or a triple of consecutive integers, for instance 1 and 567. Say that a block is odd if it starts with
an odd integer. Say that two blocks are well-separated if they have at least 3 integers between them.
For instance 123 and 567 are not well separated but 123 and 789 are well separated. Say that an
odd admissible sequence is a finite sequence of integers that decomposes into well separated odd blocks.
When we take these sequences from the set 1, ..., 2N, the notion of well separation is meant in the
cyclic sense. Thus, 1 and 2N-1 are not well separated.
Each odd admissible sequence gives rise to a monomial
in the corner invariants. This is best illustrated by
example
The sign is determined by the parity of the
number of single-digit blocks in the sequence.
The monodromy invariant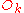 is defined as the sum of all
is defined as the sum of all
monomials coming from odd admissible sequences composed of k blocks.
The monodromy invariant is defined the same way,
is defined the same way,
with even replacing odd in the definition.
When N is odd, the allowable values of k are 1, 2, ..., (n − 1)/2. When N is even, the allowable values of k are 1, 2, ..., n/2. When k = n/2, one recovers the product invariants discussed above. In both cases, the invariants
 and
and 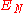 are counted
are counted
as monodromy invariants, even though they are not produced by the above construction.
The monodromy invariants are defined on the space of twisted polygons, and
restrict to give invariants on the space of closed polygons. They have
the following geometric interpretation. The monodromy M of a twisted
polygon is a certain rational function
in the corner coordinates.
The monodromy invariants are essentially the homogeneous parts of the trace
of M.
There is also a description of the monodromy invariants in terms of the (ab) coordinates. In these coordinates, the invariants arise as certain determinants of 4-diagonal matrices
.
Whenever P has all its vertices on a conic section
(such as a circle) one has
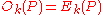 for all k.
for all k.
is an anti-symmetric linear
operator
 on the space of functions which satisfies the
on the space of functions which satisfies the
Leibniz Identity
and the Jacobi identity
.
In a 2010 paper,
Valentin Ovsienko, Richard Schwartz and Sergei Tabachnikov produced a Poisson bracket
on the space of twisted polygons
which is invariant under the pentagram map. They also showed that monodromy invariants commute with respect to this
bracket. This is to say that
for all indices.
Here is a description of the invariant Poisson bracket in terms of the variables.
There is also a description in terms of the (ab) coordinates, but it is more
complicated.
Here is an alternate description of the invariant bracket.
Given any function on the moduli space, we have the so-called
on the moduli space, we have the so-called
Hamiltonian vector field
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the pentagram map is a discrete dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
on the moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
of polygons in the projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
. The pentagram
Pentagram
A pentagram is the shape of a five-pointed star drawn with five straight strokes...
map takes a given polygon, finds the intersections of the shortest diagonals of the polygon, and constructs a new polygon from these intersections.
Richard Schwartz
Richard Schwartz
Richard Evan Schwartz is an American mathematician notable for his contributions to geometric group theory and to an area of mathematics known as billiards...
introduced the pentagram map for a general polygon in a 1992 paper
though it seems that the special case, in which
the map is defined for pentagons only, goes back at
least to a 1945 paper of Theodore Motzkin
Theodore Motzkin
Theodore Samuel Motzkin was an Israeli-American mathematician.- Biography :Motzkin's father, Leo Motzkin, was a noted Russian Zionist leader.Motzkin received his Ph.D...
.
The pentagram map is similar in spirit to the constructions underlying Desargues' Theorem
Desargues' theorem
In projective geometry, Desargues' theorem, named in honor of Gérard Desargues, states:Denote the three vertices of one triangle by a, b, and c, and those of the other by A, B, and C...
and Poncelet's porism
Poncelet's porism
In geometry, Poncelet's porism, named after French engineer and mathematician Jean-Victor Poncelet, states the following: Let C and D be two plane conics...
. It echoes the rationale and construction underlying a conjecture of Branko Grünbaum
Branko Grünbaum
Branko Grünbaum is a Croatian-born mathematician and a professor emeritus at the University of Washington in Seattle. He received his Ph.D. in 1957 from Hebrew University of Jerusalem in Israel....
concerning
the diagonals of a polygon.
Basic construction
Suppose that the verticesVertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
of the polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
P are given by
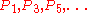 The image of P under the pentagram map is the
The image of P under the pentagram map is thepolygon Q with vertices
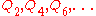 as shown in the figure. Here
as shown in the figure. Here 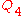 is the intersection of the diagonals
is the intersection of the diagonals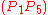 and
and 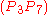 , and so on.
, and so on.On a basic level, one can think of the pentagram map as an operation defined on convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
polygons in the plane. From a more
sophisticated point of view,
the pentagram map is defined for a polygon contained in the projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
provided that
the vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
are in sufficiently general position
General position
In algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
.
The pentagram map commutes with projective transformations and thereby induces a mapping
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
on the
moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
of projective equivalence classes of polygons.
Labeling conventions
The map is slightly problematic, in the sense that the
is slightly problematic, in the sense that theindices of the P-vertices are naturally odd integers whereas the indices of
Q-vertices are naturally even
integers. A more conventional approach to the labeling would be to label the
vertices of P and Q by integers of the same parity. One can arrange this
either by adding or subtracting 1 from each of the indices of the Q-vertices.
Either choice is equally canonical. An even more conventional choice
would be to label the vertices of P and Q by consecutive integers, but
again there are 2 natural choices for how to align these labellings:
Either
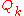 is just clockwise from
is just clockwise from 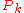
or just counterclockwise. In most papers on the subject, some choice
is made once and for all at the beginning of the paper and then the
formulas are tuned to that choice.
There is a perfectly natural way to label the vertices of the
second iterate of the pentagram map by consecutive integers. For
this reason, the second iterate of the pentagram map is more
naturally considered as an iteration defined on labeled polygons.
See the figure.
Twisted polygons
The pentagram map is also defined on the larger space oftwisted polygons.
A twisted N-gon is a bi-infinite sequence of
points in the projective plane that is N-periodic modulo a projective transformation
That is, some projective transformation M carries
 to
to  for all k.
for all k.The map M is called the monodromy
Monodromy
In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology and algebraic and differential geometry behave as they 'run round' a singularity. As the name implies, the fundamental meaning of monodromy comes from 'running round singly'...
of the twisted N-gon.
When M is the identity, a twisted N-gon can be interpreted
as an ordinary N-gon whose vertices have been listed
out repeatedly. Thus, a twisted N-gon is a generalization
of an ordinary N-gon.
Two twisted N-gons are equivalent if a projective transformation
carries one to the other. The moduli space of
twisted N-gons is the set of equivalence classes of
twisted N-gons. The space of twisted N-gons contains
the space of ordinary N-gons as a sub-variety of
co-dimension 8.
Action on pentagons and hexagons
The pentagram map is the identity on the moduli space of pentagonPentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
s.
This is to say that there is always a projective transformation carrying a
pentagon to its image under the pentagram map. It
is very likely that this (easy) result was known to the 19th century projective geometers.
Indeed, one can deduce this result from a theorem
of Darboux
Jean Gaston Darboux
Jean-Gaston Darboux was a French mathematician.-Life:Darboux made several important contributions to geometry and mathematical analysis . He was a biographer of Henri Poincaré and he edited the Selected Works of Joseph Fourier.Darboux received his Ph.D...
concerning Poncelet
Jean-Victor Poncelet
Jean-Victor Poncelet was a French engineer and mathematician who served most notably as the commandant general of the École Polytechnique...
polygons
The map
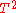 is the identity on the space of labeled
is the identity on the space of labeledhexagons.
Here T is the second iterate of the pentagram map, which
acts naturally on labeled hexagons, as described above. This
is to say that the hexagons
 and
and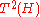 are equivalent by a label-preserving
are equivalent by a label-preservingprojective transformation. More precisely, the
hexagons
 and
and 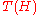 are
areprojectively equivalent, where
 is the labeled
is the labeledhexagon obtained from
 by shifting the labels by 3.
by shifting the labels by 3.See the figure.
It seems entirely possible that this fact was also known
in the 19th century.
The action of the pentagram map on pentagons and hexagons is similar in spirit to
classical configuration theorems in projective geometry such as Pascal's theorem
Pascal's theorem
In projective geometry, Pascal's theorem states that if an arbitrary hexagon is inscribed in any conic section, and pairs of opposite sides are extended until they meet, the three intersection points will lie on a straight line, the Pascal line of that configuration.- Related results :This theorem...
,
Desargues's theorem and others.
Exponential shrinking
The iterates of the pentagram map shrink any convexConvex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
exponentially fast to a point.
This is to say that the diameter of
the nth iterate of a convex polygon is less than
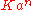
for constants
 and
and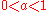 which depend
which dependon the initial polygon.
Here we are taking about the geometric
action on the polygons themselves, not on the moduli
space of projective equivalence classes of polygons.
Motivating discussion
This section is meant to give a non-technical overview for much of the remainder of the article.The context for the pentagram map is projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
.
Projective geometry is the geometry of our vision. When one looks at the top of a glass,
which is a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, one typically sees an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
. When one looks at a rectangular
door, one sees a typically non-rectangular quadrilateral
Quadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
. Projective transformations convert between the
various shapes one can see when looking at same object from different points of view. This is why it
plays such an important role in old topics like perspective drawing and new ones like computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
.
Projective geometry is built around the fact that a straight line
Line
- Science and technology :* Line , a circuit or loop.** A power line for electric power transmission** line power or lines power, domestic mains electricity.** telephone line** RF transmission line...
looks
like a straight line from any perspective. The straight lines are the building blocks for the subject.
The pentagram map is defined entirely in terms of points and straight lines.
This makes it adapted to projective geometry. If you look at the pentagram
map from another point of view (i.e., you tilt the paper on which it is drawn) then
you are still looking at the pentagram map. This explains the statement that the
pentagram map commutes with projective transformations.
The pentagram map is fruitfully considered as a mapping
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
on the
moduli space of polygons.
A moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
is an auxiliary space whose points index other objects.
For example, in Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, the sum of the angles of a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
is
always 180 degrees. You can specify a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
(up to scale) by giving
3 positive numbers,
 such that
such that 
So, each point
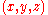 , satisfying the constraints just mentioned,
, satisfying the constraints just mentioned,indexes a triangle (up to scale). One might say that
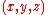 are
arecoordinates for the moduli space of scale equivalence classes of triangles.
If you want to index all possible quadrilaterals, either up to scale or not, you
would need some additional parameters. This would lead to a higher dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al
moduli space. The moduli space relevant to the pentagram map
is the moduli space of projective equivalence classes of polygons. Each point
in this space corresponds to a polygon, except that two polygons which are
different views of each other are considered the same. Since the pentagram
map is adapted to projective geometry, as mentioned above, it induces a
mapping
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
on this particular moduli space. That is, given any point
in the moduli space, you can apply the pentagram map to the corresponding
polygon and see what new point you get.
The reason for considering what the pentagram map does to the moduli
space is that it gives more salient features of the map. If you just watch,
geometrically, what happens to an individual polygon, say a convex
Convex
'The word convex means curving out or bulging outward, as opposed to concave. Convex or convexity may refer to:Mathematics:* Convex set, a set of points containing all line segments between each pair of its points...
polygon, then repeated application shrinks the polygon to a point.
To see things more clearly, you might dilate the shrinking family of
polygons so that they all have, say, the same area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
. If you do this,
then typically you will see that the family of polygons gets long and
thin. Now you can change the aspect ratio
Aspect ratio
The aspect ratio of a shape is the ratio of its longer dimension to its shorter dimension. It may be applied to two characteristic dimensions of a three-dimensional shape, such as the ratio of the longest and shortest axis, or for symmetrical objects that are described by just two measurements,...
so as to try to get yet a better view of these polygons. If you do this
process as systematically as possible, you find that you are simply
looking at what happens to points in the moduli space. The attempts
to zoom in to the picture in the most perceptive possible way lead
to the introduction of the moduli space.
To explain how the pentagram map acts on the moduli space, one must say a few words about the torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
.
One way to roughly define the torus is to say that it is the surface of an idealized donut
DONUT
DONUT was an experiment at Fermilab dedicated to the search for tau neutrino interactions. Even though the detector operated only during a few months in the summer of 1997, it was largely successful. By detecting the tau neutrino, it confirmed the existence of the last lepton predicted by the...
.
Another way is that it is the playing field for the Asteroids video game.
yet another way to describe the torus is to say that it is a computer screen with wrap, both left-to-right
and up-to-down.
The torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
is a classical example of what is known in mathematics as a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
.
This is a space that looks kind of like ordinary Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
at each point, but
somehow is hooked together differently. A sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
is another example of a manifold.
This is why it took people so long to figure out that the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
was not flat; on
small scales one cannot easily distinguish a sphere from a plane
Plane
-Physical objects:* Aeroplane or airplane, a fixed-wing aircraft* Plane , a woodworking tool to smooth surfaces* Platanus, a genus of trees with the common name "plane"* Acer pseudoplatanus, a tree species sometimes called "plane"...
. So, too, with
manifolds like the torus. There are higher dimensional tori as well.
You could imagine playing Asteroids in your room, where you can freely go through
the walls and ceiling/floor, popping out on the opposite side.
One can do experiments with the pentagram map, where one looks at how
this mapping acts on the moduli space of polygons. One starts with a point
and just traces what happens to it as the map is applied over and over
again. One sees a surprising thing: These points seem to line up along
multi-dimensional tori. These invisible tori fill
up the moduli space sort of like the way
the layers of an onion fill up the onion itself, or how the
individual cards in a deck fill up the deck. The technical statement
is that the tori make a foliation
Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
of the moduli space. The
tori have half the dimension of the moduli space. For instance,
the moduli space of
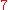 -gons is
-gons is 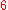 dimensional and the
dimensional and thetori in this case are
 dimensional.
dimensional.The tori are invisible subsets of the moduli space. They are
only revealed when one does the pentagram map and watches a point
move round and round, filling up one of the tori.
Roughly speaking, when dynamical systems have these invariant
tori, they are called integrable systems.
Most of the results in this article have to
do with establishing that the pentagram map is an integrable system, that
these tori really exist.
The monodromy invariants, discussed
below, turn out to be the equations for the tori. The Poisson bracket, discussed below,
is a more sophisticated math gadget that sort of encodes the local geometry
of the tori. What is nice is that the various objects fit together exactly, and
together add up to a proof that this torus motion really exists.
Cross-ratio
When the field underlying all the constructions is F, the affine line is just a copy of F. The affine line is a subset of the projective lineProjective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
. Any finite list of points in the projective line can be moved into the affine
line by a suitable projective transformation.
Given the four points
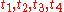 in the affine line one
in the affine line onedefines the (inverse) cross ratio
Most authors consider 1/X to be the cross-ratio
Cross-ratio
In geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
, and that is why X is called the inverse cross ratio. The inverse cross ratio is invariant under projective transformations and thus makes sense for points in the projective line. However,
the formula above only makes sense for points in the affine line.
In the slightly more general set-up below, the cross ratio makes sense
for any four collinear points in projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
One just identifies the
line containing the points with the projective line by a suitable projective transformation and then uses the formula above.
The result is independent of any choices made in the identification.
The inverse cross ratio is used in order to define a coordinate system on the moduli space
of polygons, both ordinary and twisted.
The corner coordinates
The corner invariants are basic coordinates on the space of twisted polygons.Suppose that P is a polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
. A flag of P is a pair (p,L), where p is a vertex of P and L is an adjacent line of P.
Each vertex of P is involved in 2 flags, and likewise each edge of P is involved in 2 flags.
The flags of P are ordered according to the orientation of P, as shown in the figure.
In this figure, a flag is represented by a thick arrow. Thus, there are 2N flags associated
to an N-gon.
Let P be an N-gon, with flags

To each flag F, we associate the inverse cross ratio of the points
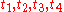 shown in the figure
shown in the figureat left.
In this way, one associates numbers
 to an n-gon. If two n-gons are
to an n-gon. If two n-gons arerelated by a projective transformation, they get the same coordinates. Sometimes the
variables
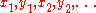 are used in place of
are used in place of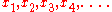
The corner invariants make sense on the moduli space of twisted polygons.
When one defines the corner invariants of a twisted polygon, one obtains
a 2N-periodic bi-infinite sequence of numbers. Taking one period
of this sequence identifies a twisted N-gon with a point
in
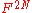 where F is the underlying field.
where F is the underlying field.Conversely, given almost any (in the sense of measure theory) point in
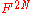 one can construct a twisted N-gon having
one can construct a twisted N-gon havingthis list of corner invariants. Such a list will not always give rise
to an ordinary polygon; there are an additional 8 equations which
the list must satisfy for it to give rise to an ordinary N-gon.
(ab) coordinates
There is a second set of coordinates for the moduli space of twisted polygons,developed by Sergei Tabachnikov and Valentin Ovsienko.
One describes a polygon in the projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
by a sequence of vectors
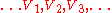 in
in so that each consecutive triple of vectors
so that each consecutive triple of vectorsspans a parallelopiped having unit volume. This leads to the
relation
The coordinates
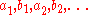
serve as coordinates for the moduli space of twisted
N-gons as long as N is not divisible by 3.
The (ab) coordinates bring out the close analogy between twisted polygons
and solutions of 3rd order linear ordinary differential equations, normalized
to have unit Wronskian
Wronskian
In mathematics, the Wronskian is a determinant introduced by and named by . It is used in the study of differential equations, where it can sometimes be used to show that a set of solutions is linearly independent.-Definition:...
.
As a birational mapping
Here is a formula for the pentagram map, expressed incorner coordinates. The
equations work more gracefully when one considers the second
iterate of the pentagram map, thanks to the
canonical labelling scheme discussed above. The second iterate of the
pentagram map is the composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
 .
.The maps
 and
and  are birational mappings
are birational mappingsof order 2, and have the following action.
where
(Note: the index 2k+0 is just 2k. The 0 is added to align the formulas.)
In these coordinates, the pentagram map is a birational mapping of
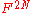
As grid compatibility relations
The formula for the pentagram map has a convenient interpretation asa certain compatibility rule for labelings on the edges of triangular grid,
as shown in the figure. In this interpretation, the corner invariants of a polygon
P label the non-horizontal edges of a single row, and then the non-horizontal
edges of subsequent rows are labeled by the corner invariants of
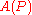 ,
,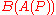 ,
,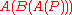 ,
,and so forth. the compatibility rules are
- c=1-ab
- wx=yz
These rules are meant to hold for all configurations which are
congruent
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
to the ones shown in the figure.
In other words, the figures involved in the relations can be
in all possible positions and orientations.
The labels on the horizontal edges are simply
auxiliary variables introduced to make the formulas simpler.
Once a single row of non-horizontal edges is provided,
the remaining rows are uniquely determined by the
compatibility rules.
Corner coordinate products
It follows directly from the formula for the pentagram map, in terms of corner coordinates,that the two quantities
are invariant under the pentagram map.
This observation is closely related to the 1991 paper of Joseph Zaks
concerning the diagonals of a polygon.
When N = 2k is even, the functions
are likewise seen, directly from the formula, to be invariant
functions. All these products turn out
to be Casimir invariant
Casimir invariant
In mathematics, a Casimir invariant or Casimir operator is a distinguished element of the centre of the universal enveloping algebra of a Lie algebra...
s with respect to the invariant
Poisson bracket discussed below. At the same time,
the functions
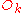 and
and  are
arethe simplest examples of the monodromy invariants defined below.
The level sets of the function
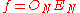 are compact
are compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, when f is restricted to
the moduli space of real convex
Convex
'The word convex means curving out or bulging outward, as opposed to concave. Convex or convexity may refer to:Mathematics:* Convex set, a set of points containing all line segments between each pair of its points...
polygons.
Hence, each orbit
of the pentagram map acting on this space has a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
closure
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
.
Volume form
The pentagram map, when acting on the moduli space X ofconvex
Convex
'The word convex means curving out or bulging outward, as opposed to concave. Convex or convexity may refer to:Mathematics:* Convex set, a set of points containing all line segments between each pair of its points...
polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
s, has an invariant volume form
Volume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
.
At the same time, as was already mentioned, the function
 has
hascompact
Compact
Compact as used in politics may refer broadly to a pact or treaty; in more specific cases it may refer to:* Interstate compact* Compact government, a type of colonial rule utilized in British North America...
level sets on X. These two properties combine with the
Poincare recurrence theorem
Poincaré recurrence theorem
In mathematics, the Poincaré recurrence theorem states that certain systems will, after a sufficiently long time, return to a state very close to the initial state. The Poincaré recurrence time is the length of time elapsed until the recurrence. The result applies to physical systems in which...
to imply that the action of the
pentagram map on X is recurrent: The orbit of almost any equivalence class
of convex polygon P returns infinitely often to every neighborhood of P.
This is to say that, modulo projective transformations, one typically
sees nearly the same shape, over and over again, as one iterates
the pentagram map.
(It is important to remember that one is considering the projective
equivalence classes of convex polygons. The fact that the pentagram map
visibly shrinks a convex polygon is irrelevant.)
It is worth mentioning that the recurrence result is
subsumed by the complete integrability results discussed below.
Monodromy invariants
The so-called monodromy invariants are a collection of functionsFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
on the moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
that are invariant under the pentagram map.
With a view towards defining the monodromy invariants,
say that a block is either a single integer
or a triple of consecutive integers, for instance 1 and 567. Say that a block is odd if it starts with
an odd integer. Say that two blocks are well-separated if they have at least 3 integers between them.
For instance 123 and 567 are not well separated but 123 and 789 are well separated. Say that an
odd admissible sequence is a finite sequence of integers that decomposes into well separated odd blocks.
When we take these sequences from the set 1, ..., 2N, the notion of well separation is meant in the
cyclic sense. Thus, 1 and 2N-1 are not well separated.
Each odd admissible sequence gives rise to a monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
in the corner invariants. This is best illustrated by
example
- 1567 gives rise to

- 123789 gives rise to

The sign is determined by the parity of the
number of single-digit blocks in the sequence.
The monodromy invariant
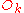 is defined as the sum of all
is defined as the sum of allmonomials coming from odd admissible sequences composed of k blocks.
The monodromy invariant
 is defined the same way,
is defined the same way,with even replacing odd in the definition.
When N is odd, the allowable values of k are 1, 2, ..., (n − 1)/2. When N is even, the allowable values of k are 1, 2, ..., n/2. When k = n/2, one recovers the product invariants discussed above. In both cases, the invariants
 and
and 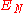 are counted
are countedas monodromy invariants, even though they are not produced by the above construction.
The monodromy invariants are defined on the space of twisted polygons, and
restrict to give invariants on the space of closed polygons. They have
the following geometric interpretation. The monodromy M of a twisted
polygon is a certain rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
in the corner coordinates.
The monodromy invariants are essentially the homogeneous parts of the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of M.
There is also a description of the monodromy invariants in terms of the (ab) coordinates. In these coordinates, the invariants arise as certain determinants of 4-diagonal matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
.
Whenever P has all its vertices on a conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
(such as a circle) one has
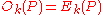 for all k.
for all k.Poisson bracket
A Poisson bracketPoisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
is an anti-symmetric linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
operator
 on the space of functions which satisfies the
on the space of functions which satisfies theLeibniz Identity
Derivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
and the Jacobi identity
Jacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
.
In a 2010 paper,
Valentin Ovsienko, Richard Schwartz and Sergei Tabachnikov produced a Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
on the space of twisted polygons
which is invariant under the pentagram map. They also showed that monodromy invariants commute with respect to this
bracket. This is to say that
for all indices.
Here is a description of the invariant Poisson bracket in terms of the variables.
-
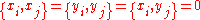 for all other
for all other 
There is also a description in terms of the (ab) coordinates, but it is more
complicated.
Here is an alternate description of the invariant bracket.
Given any function
 on the moduli space, we have the so-called
on the moduli space, we have the so-calledHamiltonian vector field
Hamiltonian vector field
In mathematics and physics, a Hamiltonian vector field on a symplectic manifold is a vector field, defined for any energy function or Hamiltonian. Named after the physicist and mathematician Sir William Rowan Hamilton, a Hamiltonian vector field is a geometric manifestation of Hamilton's equations...
-

where a summation over the repeated indices is understood.
Then
The first expression is the directional derivativeDirectional derivativeIn mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
of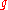 in the direction of the vector field
in the direction of the vector field 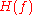 .
.
In practical terms, the fact that the monodromy invariants Poisson-commute means that the
corresponding Hamiltonian vector fields define commuting flows.
Arnold–Liouville integrability
The monodromy invariants and the invariant bracket combine to establish
Arnold–Liouville integrability of the pentagram map on the space
of twisted N-gons.
The situation is easier to describe for N odd.
In this case, the two products
are Casimir invariantCasimir invariantIn mathematics, a Casimir invariant or Casimir operator is a distinguished element of the centre of the universal enveloping algebra of a Lie algebra...
s for the bracket, meaning (in this context) that
for all functions f.
A Casimir level setLevel setIn mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....
is the set of all points in the space having
a specified value for both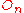 and
and  .
.
Each Casimir level set has an iso-monodromy foliationFoliationIn mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
, namely, a
decomposition into the common level sets of the remaining monodromy functions.
The Hamiltonian vector fields associated to the remaining monodromy invariants generically
span the tangent distribution to the iso-monodromy foliation. The fact that the
monodromy invariants Poisson-commute means that these vector fields
define commuting flows. These flows in turn define local coordinate charts
on each iso-monodromy level such that the transition maps are
Euclidean translations. That is, the Hamiltonian vector fields impart a
flat Euclidean structure on the iso-monodromy levels, forcing them
to be flat tori when they are smoothSmoothSmooth means having a texture that lacks friction. Not rough.Smooth may also refer to:-In mathematics:* Smooth function, a function that is infinitely differentiable; used in calculus and topology...
and compactCompactCompact as used in politics may refer broadly to a pact or treaty; in more specific cases it may refer to:* Interstate compact* Compact government, a type of colonial rule utilized in British North America...
manifolds.
This happens for almost every level set.
Since everything in sight is pentagram-invariant, the
pentagram map, restricted to an iso-monodromy leaf,
must be a translation. This kind of motion is known as
quasi-periodic motion.
This explains the Arnold-Liouville integrability.
From the point of view of symplectic geometry, the Poisson
bracket gives rise to a symplectic form on each Casimir
level set.
Algebro-geometric integrability
In a 2011 preprint,
Fedor Soloviev showed that the pentagram map has a Lax representation with a
spectral parameter, and proved its algebraic-geometric integrability. This means that the
space of polygons (either twisted or ordinary) is parametrized in terms of a
spectral curve with marked points and a
divisorDivisor (algebraic geometry)In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...
. The spectral curve is determined by the monodromy invariants, and the
divisor corresponds to a point on a torus—the Jacobi variety of the spectral curve.
The algebraic-geometric methods guarantee that the pentagram map exhibits
quasi-periodic motion on a torus (both in the twisted and the ordinary case), and
they allow one to construct explicit solutions formulas using Riemann theta functions (i.e.,
the variables that determine the polygon as explicit functions of time).
Soloviev also obtains the invariant Poisson bracket from the Krichever-Phong
universal formula.
The Octahedral recurrence
The octahedral recurrence is a dynamical system defined on the
vertices of the octahedral tiling of space. Each octahedron has
6 vertices, and these vertices are labelled in such a way that
Here
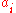 and
and 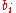 are the labels
are the labels
of antipodal vertices. A common convention is that
 always lie in a central horizontal plane
always lie in a central horizontal plane
and a_1,b_1 are the top and bottom vertices.
The octahedral recurrence is closely related to C. L. Dodgson'sLewis CarrollCharles Lutwidge Dodgson , better known by the pseudonym Lewis Carroll , was an English author, mathematician, logician, Anglican deacon and photographer. His most famous writings are Alice's Adventures in Wonderland and its sequel Through the Looking-Glass, as well as the poems "The Hunting of the...
method of condensation for computing determinants.
Typically one labels two horizontal layers of the tiling and
then uses the basic rule to let the labels propagate dynamically.
Max Glick used the cluster algebraCluster algebraCluster algebras are a class of commutative rings introduced by . A cluster algebra of rank n is an integral domain A, together with some subsets of size n called clusters whose union generates the algebra A and which satisfy various conditions....
formalism to find formulas for the iterates
of the pentagram map in terms of alternating sign matricesAlternating sign matrixIn mathematics, an alternating sign matrix is a square matrix of 0s, 1s, and −1s such that the sum of each row and column is 1 and the nonzero entries in each row and column alternate in sign. These matrices arise naturally when using Dodgson condensation to compute a determinant...
. These formulas
are similar in spirit to the formulas found by David P. RobbinsDavid P. RobbinsDavid P. Robbins was an American mathematician. He is most famous for introducing alternating sign matrices and his work on generalized Heron's formula....
and Harold Rumsey for the
iterates of the octahedral recurrence.
Alternatively, the following construction relates the octahedral recurrence
directly to the pentagram map.
Let be the octahedral tiling. Let
be the octahedral tiling. Let
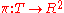 be the linear projection
be the linear projection
which maps each octahedron in to the configuration of
to the configuration of
6 points shown in the first figure.
Say that an adapted labeling of is
is
a labeling so that all points in the (infinite) inverse image of any point
in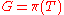 get the same numerical label.
get the same numerical label.
The octahedral recurrence applied to an adapted labeling
is the same as a recurrence on
in which the same rule as for the octahedral recurrence
is applied to every configuration of points congruentIsometryIn mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
to the configuration in the first figure. Call this the
planar octahedral recurrence.
Given a labeling of which obeys the
which obeys the
planar octahedral recurrence, one can create a labeling of the edges of
 by applying the rule
by applying the rule
to every edge. This rule refers to the figure at right
and is meant to apply to every configuration that
is congruentIsometryIn mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
to the two shown.
When this labeling is done, the edge-labeling
of G satisfies the relations for the pentagram map.
The Boussinesq equation
The continuous limit of a convex polygon is a parametrized convex curve in the plane. When the time parameter is suitably chosen, the continuous limit of the pentagram map is the classical Boussinesq equation. This equation is a classical example of an
integrable partial differential equationPartial differential equationIn mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
.
Here is a description of the geometric action of the Boussinesq equation.
Given a locally convex curve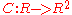 , and real numbers x and t, we consider the chordChord (geometry)A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
, and real numbers x and t, we consider the chordChord (geometry)A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
connecting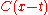 to
to 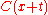 . The envelop of all these chords is a new curve
. The envelop of all these chords is a new curve
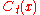 . When t is extremely small, the curve
. When t is extremely small, the curve 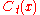 is a good model for the time t evolution of the original curve
is a good model for the time t evolution of the original curve 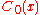 under the Boussinesq equation. This geometric description makes it fairly
under the Boussinesq equation. This geometric description makes it fairly
obvious that the B-equation is the continuous limit of the pentagram map.
At the same time, the pentagram invariant bracket is a discretization of a well known invariant Poisson bracket associated to the Boussinesq equation.
Recently, there has been some work on higher dimensional generalizations of the pentagram map and its connections
to Boussinesq-type partial differential equations
Projectively natural evolution
The pentagram map and the Boussinesq equation are examples of
projectively natural geometric evolution equations. Such equations arise
in diverse fields of mathematics, such as projective geometryProjective geometryIn mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
and computer visionComputer visionComputer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
.
Cluster algebras
In a 2010 paper
Max Glick identified the pentagram map as a special case of a
cluster algebraCluster algebraCluster algebras are a class of commutative rings introduced by . A cluster algebra of rank n is an integral domain A, together with some subsets of size n called clusters whose union generates the algebra A and which satisfy various conditions....
.