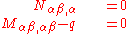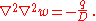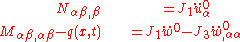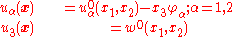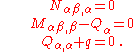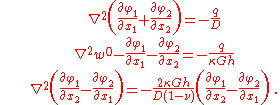Plate theory
Encyclopedia

Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
, plate theories are mathematical descriptions of the mechanics of flat plates that draws on the theory of beams
Bending
In engineering mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element. The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically...
. Plates are defined as plane structural elements with a small thickness compared to the planar dimensions . The typical thickness to width ratio of a plate structure is less than 0.1. A plate theory takes advantage of this disparity in length scale to reduce the full three-dimensional solid mechanics
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
problem to a two-dimensional problem. The aim of plate theory is to calculate the deformation
Deformation
In materials science, deformation is a change in the shape or size of an object due to an applied force or a change in temperature...
and stresses in a plate subjected to loads.
Of the numerous plate theories that have been developed since the late 19th century, two are widely accepted and used in engineering. These are
- the KirchhoffGustav KirchhoffGustav Robert Kirchhoff was a German physicist who contributed to the fundamental understanding of electrical circuits, spectroscopy, and the emission of black-body radiation by heated objects...
–LoveAugustus Edward Hough LoveAugustus Edward Hough Love FRS , often known as A. E. H. Love, was a mathematician famous for his work on the mathematical theory of elasticity...
theory of plates (classical plate theory) - The Mindlin–Reissner theory of plates (first-order shear plate theory)
Kirchhoff–Love theory for thin plates
The KirchhoffGustav Kirchhoff
Gustav Robert Kirchhoff was a German physicist who contributed to the fundamental understanding of electrical circuits, spectroscopy, and the emission of black-body radiation by heated objects...
–Love
Augustus Edward Hough Love
Augustus Edward Hough Love FRS , often known as A. E. H. Love, was a mathematician famous for his work on the mathematical theory of elasticity...
theory is an extension of Euler–Bernoulli beam theory to thin plates. The theory was developed in 1888 by Love. using assumptions proposed by Kirchhoff. It is assumed that there a mid-surface plane can be used to represent the three-dimensional plate in two dimensional form.
The following kinematic assumptions that are made in this theory:
- straight lines normal to the mid-surface remain straight after deformation
- straight lines normal to the mid-surface remain normal to the mid-surface after deformation
- the thickness of the plate does not change during a deformation.
Displacement field
The Kirchhoff hypothesis implies that the displacementDisplacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
field has the form
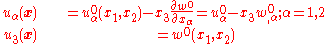
where
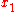 and
and 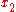 are the Cartesian coordinates on the mid-surface of the undeformed plate,
are the Cartesian coordinates on the mid-surface of the undeformed plate, 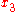 is the coordinate for the thickness direction,
is the coordinate for the thickness direction,  are the in-plane displacements of the mid-surface, and
are the in-plane displacements of the mid-surface, and 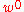 is the displacement of the mid-surface in the
is the displacement of the mid-surface in the 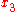 direction.
direction.If
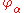 are the angles of rotation of the normal
are the angles of rotation of the normalNormal
Normal may refer to:* Normality , conformance to an average* Norm , social norms, expected patterns of behavior studied within the context of sociology* Normal distribution , the Gaussian continuous probability distribution...
to the mid-surface, then in the Kirchhoff–Love theory

Strain-displacement relations
For the situation where the strains in the plate are infinitesimal and the rotations of the mid-surface normals are less than 10 the strains-displacement relations are
the strains-displacement relations are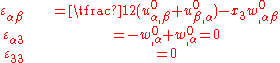
Therefore the only non-zero strains are in the in-plane directions.
If the rotations of the normals to the mid-surface are in the range of 10
 to 15
to 15 , the strain-displacement relations can be approximated using the von Kármán
, the strain-displacement relations can be approximated using the von KármánTheodore von Karman
Theodore von Kármán was a Hungarian-American mathematician, aerospace engineer and physicist who was active primarily in the fields of aeronautics and astronautics. He is responsible for many key advances in aerodynamics, notably his work on supersonic and hypersonic airflow characterization...
strains. Then the kinematic assumptions of Kirchhoff-Love theory lead to the following strain-displacement relations
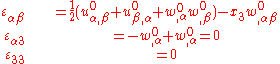
This theory is nonlinear because of the quadratic terms in the strain-displacement relations.
Equilibrium equations
The equilibrium equations for the plate can be derived from the principle of virtual work. For the situation where the strains and rotations of the plate are small, the equilibrium equations for an unloaded plate are given by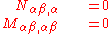
where the stress resultants and stress moment resultants are defined as
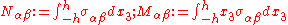
and the thickness of the plate is
 . The quantities
. The quantities 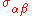 are the stresses.
are the stresses.If the plate is loaded by an external distributed load
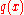 that is normal to the mid-surface and directed in the positive
that is normal to the mid-surface and directed in the positive 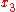 direction, the principle of virtual work then leads to the equilibrium equations
direction, the principle of virtual work then leads to the equilibrium equationsFor moderate rotations, the strain-displacement relations take the von Karman form and the equilibrium equations can be expressed as

Boundary conditions
The boundary conditions that are needed to solve the equilibrium equations of plate theory can be obtained from the boundary terms in the principle of virtual work.For small strains and small rotations, the boundary conditions are
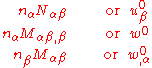
Note that the quantity
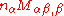 is an effective shear force.
is an effective shear force.Stress-strain relations
The stress-strain relations for a linear elastic Kirchhoff plate are given by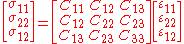
Since
 and
and 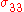 do not appear in the equilibrium equations it is implicitly assumed that these quantities do not have any effect on the momentum balance and are neglected.
do not appear in the equilibrium equations it is implicitly assumed that these quantities do not have any effect on the momentum balance and are neglected.It is more convenient to work with the stress and moment results that enter the equilibrium equations. These are related to the displacements by
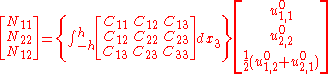
and
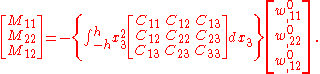
The extensional stiffnesses are the quantities
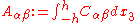
The bending stiffnesses (also called flexural rigidity) are the quantities
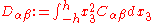
Isotropic and homogeneous Kirchhoff plate
For an isotropic and homogeneous plate, the stress-strain relations are
The moments corresponding to these stresses are
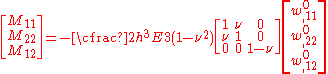
Pure bending
The displacements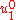 and
and 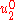 are zero under pure bending
are zero under pure bendingPure bending
Pure bending is a condition of stress where a bending moment is applied to a beam without the simultaneous application of axial, shear, or torsional forces....
conditions. For an isotropic, homogeneous plate under pure bending the governing equation is

In index notation,
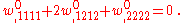
In direct tensor notation, the governing equation is
Transverse loading
For a transversely loaded plate without axial deformations, the governing equation has the form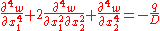
where

In index notation,
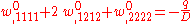
and in direct notation
In cylindrical coordinates
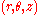 , the governing equation is
, the governing equation is
Orthotropic and homogeneous Kirchhoff plate
For an orthotropicOrthotropic material
An orthotropic material has two or three mutually orthogonal twofold axes of rotational symmetry so that its mechanical properties are, in general, different along each axis. Orthotropic materials are thus anisotropic; their properties depend on the direction in which they are measured...
plate

Therefore,

and
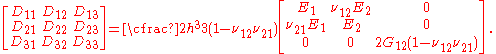
Transverse loading
The governing equation of an orthotropic Kirchhoff plate loaded transversely by a distributed load per unit area is
per unit area is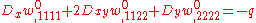
where
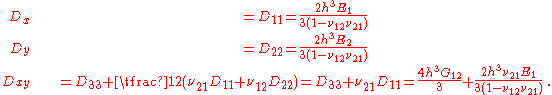
Dynamics of thin Kirchhoff plates
The dynamic theory of plates determines the propagation of waves in the plates, and the study of standing waves and vibration modes.Governing equations
The governing equations for the dynamics of a Kirchhoff–Love plate arewhere, for a plate with density
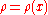 ,
,
and
The figures below show some vibrational modes of a circular plate.
Isotropic plates
The governing equations simplify considerably for isotropic and homogeneous plates for which the in-plane deformations can be neglected and have the form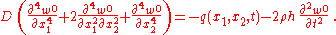
where
 is the bending stiffness of the plate. For a uniform plate of thickness
is the bending stiffness of the plate. For a uniform plate of thickness  ,
,
In direct notation
Mindlin–Reissner theory for thick plates
In the theory of thick plates, or theory of Raymond Mindlin and Eric Reissner, the normal to the mid-surface remains straight but not necessarily perpendicular to the mid-surface. If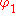 and
and 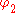 designate the angles which the mid-surface makes with the
designate the angles which the mid-surface makes with the 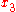 axis then
axis then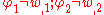
Then the Mindlin–Reissner hypothesis implies that
Strain-displacement relations
Depending on the amount of rotation of the plate normals two different approximations for the strains can be derived from the basic kinematic assumptions.For small strains and small rotations the strain-displacement relations for Mindlin–Reissner plates are
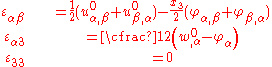
The shear strain, and hence the shear stress, across the thickness of the plate is not neglected in this theory. However, the shear strain is constant across the thickness of the plate. This cannot be accurate since the shear stress is known to be parabolic even for simple plate geometries. To account for the inaccuracy in the shear strain, a shear correction factor (
 ) is applied so that the correct amount of internal energy is predicted by the theory. Then
) is applied so that the correct amount of internal energy is predicted by the theory. Then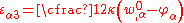
Equilibrium equations
The equilibrium equations have slightly different forms depending on the amount of bending expected in the plate. For the situation where the strains and rotations of the plate are smallthe equilibrium equations for a Mindlin–Reissner plate areThe resultant shear forces in the above equations are defined as
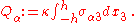
Boundary conditions
The boundary conditions are indicated by the boundary terms in the principle of virtual work.If the only external force is a vertical force on the top surface of the plate, the boundary conditions are

Constitutive relations
The stress-strain relations for a linear elastic Mindlin–Reissner plate are given by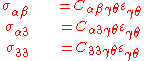
Since
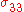 does not appear in the equilibrium equations it is implicitly assumed that it do not have any effect on the momentum balance and is neglected. This assumption is also called the plane stress assumption. The remaining stress-strain relations for an orthotropic
does not appear in the equilibrium equations it is implicitly assumed that it do not have any effect on the momentum balance and is neglected. This assumption is also called the plane stress assumption. The remaining stress-strain relations for an orthotropicOrthotropic
Orthotropic may refer to:* Orthotropic material is one that has the different materials properties or strengths in different orthogonal directions...
material, in matrix form, can be written as
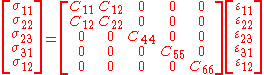
Then,

and
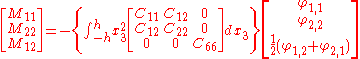
For the shear terms
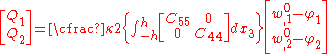
The extensional stiffnesses are the quantities
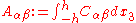
The bending stiffnesses are the quantities
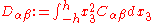
Isotropic and homogeneous Mindlin-Reissner plates
For uniformly thick, homogeneous, and isotropic plates, the stress-strain relations in the plane of the plate are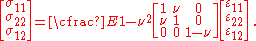
where
 is the Young's modulus,
is the Young's modulus,  is the Poisson's ratio, and
is the Poisson's ratio, and 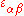 are the in-plane strains. The through-the-thickness shear stresses and strains are related by
are the in-plane strains. The through-the-thickness shear stresses and strains are related by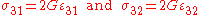
where
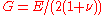 is the shear modulus.
is the shear modulus.Constitutive relations
The relations between the stress resultants and the generalized displacements for an isotropic Mindlin–Reissner plate are: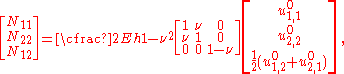

and
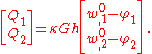
The bending rigidity is defined as the quantity
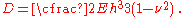
For a plate of thickness
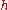 , the bending rigidity has the form
, the bending rigidity has the form
Governing equations
If we ignore the in-plane extension of the plate, the governing equations are
In terms of the generalized deformations
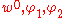 , the three governing equations are
, the three governing equations areThe boundary conditions along the edges of a rectangular plate are

Reissner–Stein theory for isotropic cantilever plates
In general, exact solutions for cantilever plates using plate theory are quite involved and few exact solutions can be found in the literature. Reissner and Stein provide a simplified theory for cantilever plates that is an improvement over older theories such as Saint-Venant plate theory.The Reissner-Stein theory assumes a transverse displacement field of the form
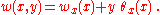
The governing equations for the plate then reduce to two coupled ordinary differential equations:
where
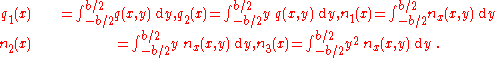
At
 , since the beam is clamped, the boundary conditions are
, since the beam is clamped, the boundary conditions are
The boundary conditions at
 are
are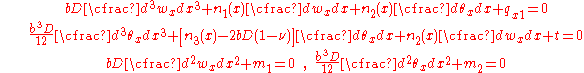
where
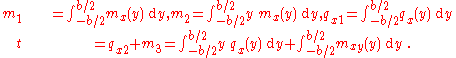
| Derivation of Reissner–Stein cantilever plate equations |
|---|
is given by where  is the transverse displacement, is the transverse displacement,  is the length, is the length,  is the width, is the width,  is the Poisson's is the Poisson'sratio,  is the Young's modulus, and is the Young's modulus, and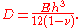 The potential energy of transverse loads 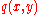 (per unit length) is (per unit length) is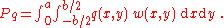 The potential energy of in-plane loads 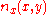 (per unit width) is (per unit width) is The potential energy of tip forces  (per unit width), and bending moments (per unit width), and bending moments 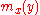 and and 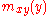 (per unit width) is 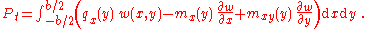 A balance of energy requires that the total energy is  With the Reissener–Stein assumption for the displacement, we have 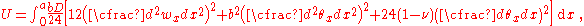  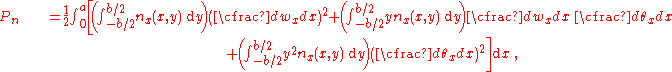 and 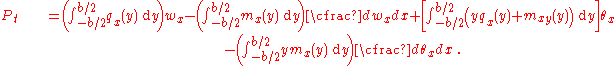 Taking the first variation of  with respect to with respect to  and andsetting it to zero gives us the Euler equations  and 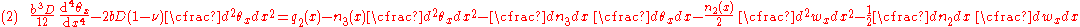 where  Since the beam is clamped at  , we have , we have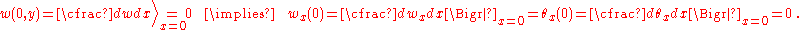 The boundary conditions at  can be found by integration by parts: can be found by integration by parts: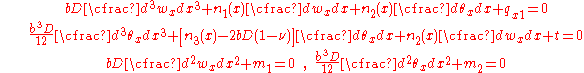 where 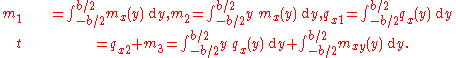 |
See also
- Bending of platesBending of platesBending of plates or plate bending refers to the deflection of a plate perpendicular to the plane of the plate under the action of external forces and moments. The amount of deflection can be determined by solving the differential equations of an appropriate plate theory. The stresses in the...
- Vibration of platesVibration of platesThe vibration of plates is a special case of the more general problem of mechanical vibrations. The equations governing the motion of plates are simpler than those for general three-dimensional objects because one of the dimensions of a plate is much smaller than the other two...
- Infinitesimal strain theory
- Finite strain theory
- Stress (mechanics)
- Linear elasticityLinear elasticityLinear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
- BendingBendingIn engineering mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element. The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically...
- Euler–Bernoulli beam equation
- Timoshenko beam theoryTimoshenko beam theoryThe Timoshenko beam theory was developed by Ukrainian-born scientist Stephen Timoshenko in the beginning of the 20th century. The model takes into account shear deformation and rotational inertia effects, making it suitable for describing the behaviour of short beams, sandwich composite beams or...