The vibration of plates is a special case of the more general problem of mechanical vibration

Vibration

Vibration refers to mechanical oscillations about an equilibrium point. The oscillations may be periodic such as the motion of a pendulum or random such as the movement of a tire on a gravel road.Vibration is occasionally "desirable"...

s. The equations governing the motion of plates are simpler than those for general three-dimensional objects because one of the dimensions of a plate is much smaller than the other two. This suggests that a two-dimensional plate theory

Plate theory

In continuum mechanics, plate theories are mathematical descriptions of the mechanics of flat plates that draws on the theory of beams. Plates are defined as plane structural elements with a small thickness compared to the planar dimensions . The typical thickness to width ratio of a plate...

 will give an excellent approximation to the actual three-dimensional motion of a plate-like object, and indeed that is found to be true.

There are several theories that have been developed to describe the motion of plates. The most commonly used are the Kirchhoff-Love theory

Kirchhoff–Love plate theory

The Kirchhoff–Love theory of plates is a two-dimensional mathematical model that is used to determine the stresses and deformations in thin plates subjected to forces and moments. This theory is an extension of Euler-Bernoulli beam theory and was developed in 1888 by Love using assumptions...

 and the
Mindlin-Reissner theory

Mindlin–Reissner plate theory

The Mindlin-Reissner theory of plates is an extension of Kirchhoff–Love plate theory that takes into account shear deformations through-the-thickness of a plate. The theory was proposed in 1951 by Raymond Mindlin . A similar, but not identical, theory had been proposed earlier by Eric Reissner in...

. Solutions to the governing equations predicted by these theories can give us insight into the behavior of plate-like objects both under free and forced conditions. This includes
the propagation of waves and the study of standing waves and vibration modes in plates.

Kirchhoff-Love plates

The governing equations for the dynamics of a Kirchhoff-Love plate are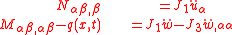
where 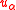are the in-plane displacements of the mid-surface of the plate, is the transverse (out-of-plane) displacement of the mid-surface of the plate, 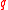is an applied transverse load, and the resultant forces and moments are defined as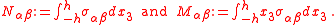
Note that the thickness of the plate is 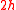and that the resultants are defined as weighted averages of the in-plane stresses 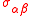. The derivatives in the governing equations are defined as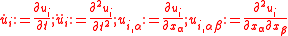
where the Latin indices go from 1 to 3 while the Greek indices go from 1 to 2. Summation over repeated indices is implied. The coordinates is out-of-plane while the coordinates 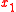and 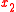are in plane.
For a uniformly thick plate of thickness 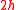and homogeneous mass density

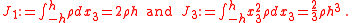
Isotropic plates

For an isotropic and homogeneous plate, the stress-strain relations are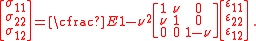
where 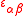are the in-plane strains. The strain-displacement relations
for Kirchhoff-Love plates are
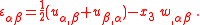
Therefore, the resultant moments corresponding to these stresses are
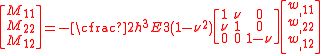
If we ignore the in-plane displacements 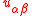, the governing equations reduce to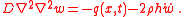

Free vibrations

For free vibrations, the governing equation of an isotropic plate is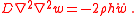

Circular plates

For freely vibrating circular plates,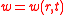 , and the Laplacian in cylindrical coordinates has the form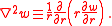
Therefore, the governing equation for free vibrations of a circular plate of thicknes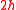s is
Expanded out,
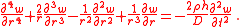
To solve this equation we use the idea of separation of variables

Separation of variables

In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....

 and assume a solution of the form
Plugging this assumed solution into the governing equation gives us
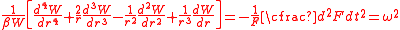
where 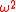is a constant and 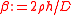. The solution of the right hand equation is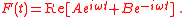
The left hand side equation can be written as
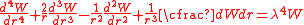
where 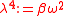. The general solution of this eigenvalue problem that is
appropriate for plates has the form
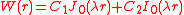
where 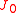is the order 0 Bessel function

Bessel function

In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...

 of the first kind and is the order 0 modified Bessel function of the first kind. The constants and are determined from the boundary conditions. For a plate of radius with a clamped circumference, the boundary conditions are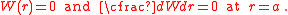
From these boundary conditions we find that
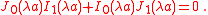
We can solve this equation for 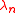(and there are an infinite number of roots) and from that find the modal frequencies 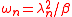. We can also express the displacement in the form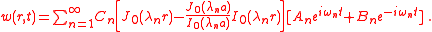
For a given frequency 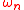the first term inside the sum in the above equation gives the mode shape. We can find the value
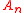of using the appropriate boundary condition at and the coefficients and 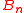from the initial conditions by taking advantage of the orthogonality of Fourier components.

Rectangular plates

Consider a rectangular plate which has dimensions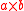 in the 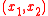-plane and thickness 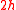in the 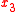-direction. We seek to find the free vibration modes of the plate.

Assume a displacement field of the form
Then,
and
Plugging these into the governing equation gives
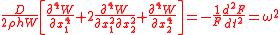
where 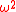is a constant because the left hand side is independent of while the right hand side is independent of 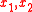. From the right hand side, we then have
From the left hand side,
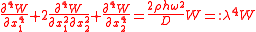
where
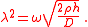
Since the above equation is a biharmonic eigenvalue problem, we look for Fourier expansion
solutions of the form
We can check and see that this solution satisfies the boundary conditions for a freely vibrating
rectangular plate with simply supported edges:
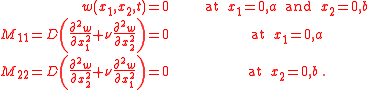
Plugging the solution into the biharmonic equation gives us
Comparison with the previous expression for indicates that we can have an infinite
number of solutions with
Therefore the general solution for the plate equation is
To find the values of and we use initial conditions and the orthogonality of Fourier components. For example, if
we get,

See also

• Bending
  Bending
  In engineering mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element. The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically...
  
  
• Bending of plates
  Bending of plates
  Bending of plates or plate bending refers to the deflection of a plate perpendicular to the plane of the plate under the action of external forces and moments. The amount of deflection can be determined by solving the differential equations of an appropriate plate theory. The stresses in the...
  
  
• Infinitesimal strain theory
• Kirchhoff–Love plate theory
  Kirchhoff–Love plate theory
  The Kirchhoff–Love theory of plates is a two-dimensional mathematical model that is used to determine the stresses and deformations in thin plates subjected to forces and moments. This theory is an extension of Euler-Bernoulli beam theory and was developed in 1888 by Love using assumptions...
  
  
• Linear elasticity
  Linear elasticity
  Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
  
  
• Mindlin–Reissner plate theory
  Mindlin–Reissner plate theory
  The Mindlin-Reissner theory of plates is an extension of Kirchhoff–Love plate theory that takes into account shear deformations through-the-thickness of a plate. The theory was proposed in 1951 by Raymond Mindlin . A similar, but not identical, theory had been proposed earlier by Eric Reissner in...
  
  
• Plate theory
  Plate theory
  In continuum mechanics, plate theories are mathematical descriptions of the mechanics of flat plates that draws on the theory of beams. Plates are defined as plane structural elements with a small thickness compared to the planar dimensions . The typical thickness to width ratio of a plate...
  
  
• Stress (mechanics)
• Structural acoustics
  Structural acoustics
  Structural acoustics is the study of the mechanical waves in structures and how they interact with and radiate into adjacent fluids. The field of structural acoustics is often referred to as vibroacoustics in Europe and Asia. People that work in the field of structural acoustics are known as...