
Timoshenko beam theory
Encyclopedia
The Timoshenko beam theory was developed by Ukrainian-born scientist Stephen Timoshenko
in the beginning of the 20th century. The model takes into account shear deformation
and rotational inertia
effects, making it suitable for describing the behaviour of short beams, sandwich composite beams
or beams subject to high-frequency
excitation when the wavelength
approaches the thickness of the beam. The resulting equation is of 4th order, but unlike ordinary beam theory - i.e. Bernoulli-Euler theory - there is also a second order spatial derivative present. Physically, taking into account the added mechanisms of deformation effectively lowers the stiffness of the beam, while the result is a larger deflection under a static load and lower predicted eigenfrequencies for a given set of boundary conditions. The latter effect is more noticeable for higher frequencies as the wavelength becomes shorter, and thus the distance between opposing shear forces decreases.
If the shear modulus of the beam material approaches infinity - and thus the beam becomes rigid in shear - and if rotational inertia effects are neglected, Timoshenko beam theory converges towards ordinary beam theory.
Timoshenko beam theory without axial effects, the displacements of the beam are assumed to be given by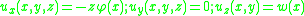
where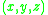 are the coordinates of a point in the beam,
are the coordinates of a point in the beam, 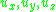 are the components of the displacement vector in the three coordinate directions,
are the components of the displacement vector in the three coordinate directions,  is the angle of rotation of the normal to the mid-surface of the beam, and
is the angle of rotation of the normal to the mid-surface of the beam, and  is the displacement of the mid-surface in the
is the displacement of the mid-surface in the  -direction.
-direction.
The governing equations are the following uncoupled system of ordinary differential equation
s: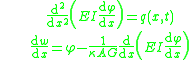
The Timoshenko beam theory for the static case is equivalent to the Euler-Bernoulli theory
when the last term above is neglected, an approximation that is valid when
where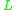 is the length of the beam.
is the length of the beam.
Combining the two equations gives, for a homogeneous beam of constant cross-section,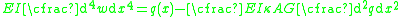
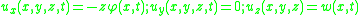
where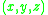 are the coordinates of a point in the beam,
are the coordinates of a point in the beam,  are the components of the displacement vector in the three coordinate directions,
are the components of the displacement vector in the three coordinate directions,  is the angle of rotation of the normal to the mid-surface of the beam, and
is the angle of rotation of the normal to the mid-surface of the beam, and  is the displacement of the mid-surface in the
is the displacement of the mid-surface in the  -direction.
-direction.
Starting from the above assumption, the Timoshenko beam theory, allowing for vibrations, may be described with the coupled linear partial differential equations :
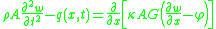
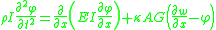
where the dependent variables are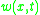 , the translational displacement of the beam, and
, the translational displacement of the beam, and 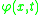 , the angular displacement. Note that unlike the Euler-Bernoulli
, the angular displacement. Note that unlike the Euler-Bernoulli
theory, the angular deflection is another variable and not approximated by the slope of the deflection. Also,
These parameters are not necessarily constants.
For a linear elastic, isotropic, homogeneous beam of constant cross-section these two equations can be combined to give
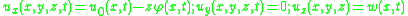
where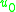 is an additional displacement in the
is an additional displacement in the  -direction, then the governing equations of a Timoshenko beam take the form
-direction, then the governing equations of a Timoshenko beam take the form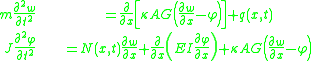
where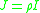 and
and  is an externally applied axial force. Any external axial force is balanced by the stress resultant
is an externally applied axial force. Any external axial force is balanced by the stress resultant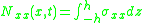
where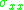 is the axial stress and the thickness of the beam has been assumed to be
is the axial stress and the thickness of the beam has been assumed to be 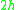 .
.
The combined beam equation with axial force effects included is
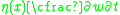
the coupled governing equations for a Timoshenko beam take the form
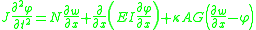
and the combined equation becomes
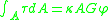
The shear coefficient is dependent to the Poisson's Ratio. The approaches of more precise expressions are made by many scientists, including Stephen Timoshenko
, Raymond D. Mindlin
, G. R. Cowper, John W. Hutchinson
, etc. In engineering practices, the expressions provided by Stephen Timoshenko
are good enough for general cases.
For solid rectangular cross-section,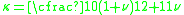
For solid circular cross-section,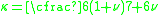
Stephen Timoshenko
Stanford University:* Bergman, E. O., * Kurzweil, A. C., * , * Huang, Y. S., * Wang, T. K., * Weber, H. S., * , * , * , -Publications:...
in the beginning of the 20th century. The model takes into account shear deformation
Shear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
and rotational inertia
Inertia
Inertia is the resistance of any physical object to a change in its state of motion or rest, or the tendency of an object to resist any change in its motion. It is proportional to an object's mass. The principle of inertia is one of the fundamental principles of classical physics which are used to...
effects, making it suitable for describing the behaviour of short beams, sandwich composite beams
Sandwich structured composite
A sandwich-structured composite is a special class of composite materials that is fabricated by attaching two thin but stiff skins to a lightweight but thick core...
or beams subject to high-frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
excitation when the wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
approaches the thickness of the beam. The resulting equation is of 4th order, but unlike ordinary beam theory - i.e. Bernoulli-Euler theory - there is also a second order spatial derivative present. Physically, taking into account the added mechanisms of deformation effectively lowers the stiffness of the beam, while the result is a larger deflection under a static load and lower predicted eigenfrequencies for a given set of boundary conditions. The latter effect is more noticeable for higher frequencies as the wavelength becomes shorter, and thus the distance between opposing shear forces decreases.
If the shear modulus of the beam material approaches infinity - and thus the beam becomes rigid in shear - and if rotational inertia effects are neglected, Timoshenko beam theory converges towards ordinary beam theory.
Quasistatic Timoshenko beam
In staticStatics
Statics is the branch of mechanics concerned with the analysis of loads on physical systems in static equilibrium, that is, in a state where the relative positions of subsystems do not vary over time, or where components and structures are at a constant velocity...
Timoshenko beam theory without axial effects, the displacements of the beam are assumed to be given by
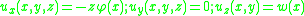
where
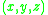 are the coordinates of a point in the beam,
are the coordinates of a point in the beam, 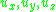 are the components of the displacement vector in the three coordinate directions,
are the components of the displacement vector in the three coordinate directions,  is the angle of rotation of the normal to the mid-surface of the beam, and
is the angle of rotation of the normal to the mid-surface of the beam, and  is the displacement of the mid-surface in the
is the displacement of the mid-surface in the  -direction.
-direction.The governing equations are the following uncoupled system of ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s:
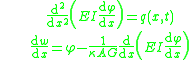
The Timoshenko beam theory for the static case is equivalent to the Euler-Bernoulli theory
Euler-Bernoulli beam equation
Euler–Bernoulli beam theory is a simplification of the linear theory of elasticity which provides a means of calculating the load-carrying and deflection characteristics of beams. It covers the case for small deflections of a beam which is subjected to lateral loads only...
when the last term above is neglected, an approximation that is valid when

where
 is the length of the beam.
is the length of the beam.Combining the two equations gives, for a homogeneous beam of constant cross-section,
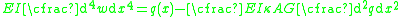
| Derivation of quasistatic Timoshenko beam equations |
|---|
From the kinematic assumptions for a Timoshenko beam, the displacements of the beam are given by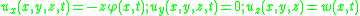 Then, from the strain-displacement relations for small strains, the non-zero strains based on the Timoshenko assumptions are 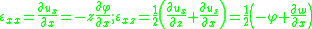 Since the actual shear strain in the beam is not constant over the cross section we introduce a correction factor  such that such that The variation in the internal energy of the beam is 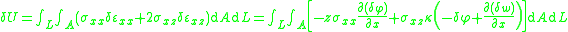 Define 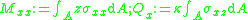 Then 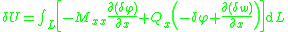 Integration by parts, and noting that because of the boundary conditions the variations are zero at the ends of the beam, leads to 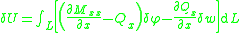 The variation in the external work done on the beam by a transverse load 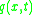 per unit length is per unit length is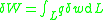 Then, for a quasistatic beam, the principle of virtual work gives 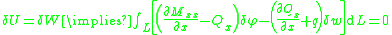 The governing equations for the beam are, from the fundamental theorem of variational calculus,  For a linear elastic beam 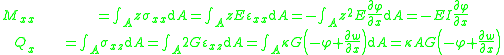 Therefore the governing equations for the beam may be expressed as 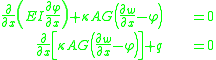 Combining the two equations together gives 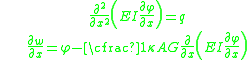 |
Dynamic Timoshenko beam
In Timoshenko beam theory without axial effects, the displacements of the beam are assumed to be given by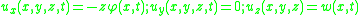
where
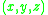 are the coordinates of a point in the beam,
are the coordinates of a point in the beam,  are the components of the displacement vector in the three coordinate directions,
are the components of the displacement vector in the three coordinate directions,  is the angle of rotation of the normal to the mid-surface of the beam, and
is the angle of rotation of the normal to the mid-surface of the beam, and  is the displacement of the mid-surface in the
is the displacement of the mid-surface in the  -direction.
-direction.Starting from the above assumption, the Timoshenko beam theory, allowing for vibrations, may be described with the coupled linear partial differential equations :
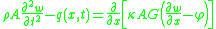
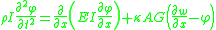
where the dependent variables are
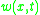 , the translational displacement of the beam, and
, the translational displacement of the beam, and 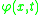 , the angular displacement. Note that unlike the Euler-Bernoulli
, the angular displacement. Note that unlike the Euler-BernoulliEuler-Bernoulli beam equation
Euler–Bernoulli beam theory is a simplification of the linear theory of elasticity which provides a means of calculating the load-carrying and deflection characteristics of beams. It covers the case for small deflections of a beam which is subjected to lateral loads only...
theory, the angular deflection is another variable and not approximated by the slope of the deflection. Also,
-
 is the densityDensityThe mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
is the densityDensityThe mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
of the beam material (but not the linear densityLinear densityLinear density, linear mass density or linear mass is a measure of mass per unit of length, and it is a characteristic of strings or other one-dimensional objects. The SI unit of linear density is the kilogram per metre...
). -
 is the cross section area.
is the cross section area. -
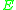 is the elastic modulusElastic modulusAn elastic modulus, or modulus of elasticity, is the mathematical description of an object or substance's tendency to be deformed elastically when a force is applied to it...
is the elastic modulusElastic modulusAn elastic modulus, or modulus of elasticity, is the mathematical description of an object or substance's tendency to be deformed elastically when a force is applied to it...
. -
 is the shear modulus.
is the shear modulus. -
 is the second moment of areaSecond moment of areaThe second moment of area, also known as the area moment of inertia, moment of inertia of plane area, or second moment of inertia is a property of a cross section that can be used to predict the resistance of beams to bending and deflection, around an axis that lies in the cross-sectional plane...
is the second moment of areaSecond moment of areaThe second moment of area, also known as the area moment of inertia, moment of inertia of plane area, or second moment of inertia is a property of a cross section that can be used to predict the resistance of beams to bending and deflection, around an axis that lies in the cross-sectional plane...
. -
 , called the Timoshenko shear coefficient, depends on the geometry. Normally,
, called the Timoshenko shear coefficient, depends on the geometry. Normally, 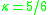 for a rectangular section.
for a rectangular section. -
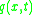 is a distributed load (force per length).
is a distributed load (force per length).
These parameters are not necessarily constants.
For a linear elastic, isotropic, homogeneous beam of constant cross-section these two equations can be combined to give

| Derivation of combined Timoshenko beam equation |
|---|
The equations governing the bending of a homogeneous Timoshenko beam of constant cross-section are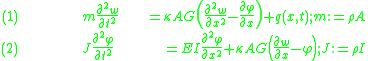 From equation (1), assuming appropriate smoothness, we have 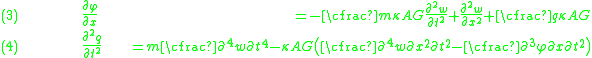 From (3), assuming appropriate smoothness, 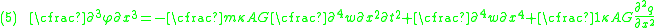 Differentiating equation (2) gives 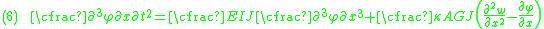 From equations (4) and (6) 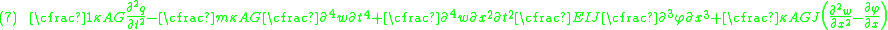 From equations (3) and (7) 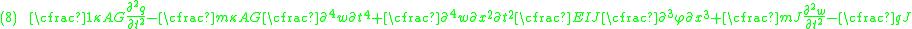 Plugging equation (5) into (8) gives  Rearrange to get 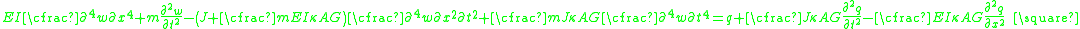 |
Axial effects
If the displacements of the beam are given by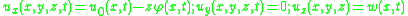
where
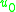 is an additional displacement in the
is an additional displacement in the  -direction, then the governing equations of a Timoshenko beam take the form
-direction, then the governing equations of a Timoshenko beam take the form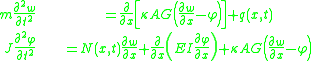
where
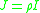 and
and  is an externally applied axial force. Any external axial force is balanced by the stress resultant
is an externally applied axial force. Any external axial force is balanced by the stress resultant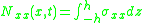
where
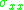 is the axial stress and the thickness of the beam has been assumed to be
is the axial stress and the thickness of the beam has been assumed to be 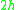 .
.The combined beam equation with axial force effects included is

Damping
If, in addition to axial forces, we assume a damping force that is proportional to the velocity with the form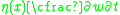
the coupled governing equations for a Timoshenko beam take the form

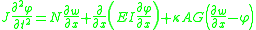
and the combined equation becomes

Shear coefficient
Determining the shear coefficient is not straightforward (nor are the determined values widely accepted, ie there's more than one answer), generally it must satisfy: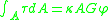
The shear coefficient is dependent to the Poisson's Ratio. The approaches of more precise expressions are made by many scientists, including Stephen Timoshenko
Stephen Timoshenko
Stanford University:* Bergman, E. O., * Kurzweil, A. C., * , * Huang, Y. S., * Wang, T. K., * Weber, H. S., * , * , * , -Publications:...
, Raymond D. Mindlin
Raymond D. Mindlin
Raymond David Mindlin was a mechanician who made seminal contributions to many branches of applied mechanics, applied physics, and engineering sciences.-Education:...
, G. R. Cowper, John W. Hutchinson
John W. Hutchinson
John W. Hutchinson is a renowned scholar in the field of applied mechanics, and has made seminal contributions to the mechanics of structures and mechanics of materials. He is a recipient of the Timoshenko Medal...
, etc. In engineering practices, the expressions provided by Stephen Timoshenko
Stephen Timoshenko
Stanford University:* Bergman, E. O., * Kurzweil, A. C., * , * Huang, Y. S., * Wang, T. K., * Weber, H. S., * , * , * , -Publications:...
are good enough for general cases.
For solid rectangular cross-section,
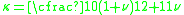
For solid circular cross-section,
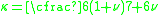
See also
- BendingBendingIn engineering mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element. The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically...
- Euler-Bernoulli beam equationEuler-Bernoulli beam equationEuler–Bernoulli beam theory is a simplification of the linear theory of elasticity which provides a means of calculating the load-carrying and deflection characteristics of beams. It covers the case for small deflections of a beam which is subjected to lateral loads only...
- Sandwich theorySandwich theorySandwich theory describes the behaviour of a beam, plate, or shell which consists of three layers - two facesheets and one core. The most commonly used sandwich theory is linear and is an extension of first order beam theory...
- Plate theoryPlate theoryIn continuum mechanics, plate theories are mathematical descriptions of the mechanics of flat plates that draws on the theory of beams. Plates are defined as plane structural elements with a small thickness compared to the planar dimensions . The typical thickness to width ratio of a plate...

