Point groups in two dimensions - AbsoluteAstronomy.com

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a two-dimensional point group
Point group
In geometry, a point group is a group of geometric symmetries that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O...

or rosette group is a group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

of geometric symmetries

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

(isometries

Isometry

In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...

) that keep at least one point fixed in a plane. Every such group is a subgroup of the orthogonal group

Orthogonal group

In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...

O(2), including O(2) itself. Its elements are rotations and reflections, and every such group containing only rotations is a subgroup of the special orthogonal group SO(2), including SO(2) itself. That group is isomorphic to R/Z and the first unitary group

Unitary group

In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...

, U(1), a group also known as the circle group.

The two-dimensional point groups are important as a basis for the axial three-dimensional point groups

Point groups in three dimensions

In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...

, with the addition of reflections in the axial coordinate. They are also important in symmetries of organisms, like starfish and jellyfish

Jellyfish

Jellyfish are free-swimming members of the phylum Cnidaria. Medusa is another word for jellyfish, and refers to any free-swimming jellyfish stages in the phylum Cnidaria...

, and organism parts, like flower

Flower

A flower, sometimes known as a bloom or blossom, is the reproductive structure found in flowering plants . The biological function of a flower is to effect reproduction, usually by providing a mechanism for the union of sperm with eggs...

Discrete groups

There are two families of discrete two-dimensional point groups, and they are specified with parameter n, which is the order of the group of the rotations in the group.

Group	Intl Hermann-Mauguin notation Hermann–Mauguin notation is used to represent the symmetry elements in point groups, plane groups and space groups. It is named after the German crystallographer Carl Hermann and the French mineralogist Charles-Victor Mauguin...	Orbifold Orbifold In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...	Coxeter Coxeter notation In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M...	Order	Description
C_n	n	nn	[n]⁺	n	Cyclic: n-fold rotations. Abstract group Z_n, the group of integers under addition modulo n.
D_n	nm	*nn	[n]	2n	Dihedral: n-fold reflections. Abstract group Dih_n, the dihedral group Dihedral group In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three... .

Intl refers to Hermann-Mauguin notation

Hermann-Mauguin notation

Hermann–Mauguin notation is used to represent the symmetry elements in point groups, plane groups and space groups. It is named after the German crystallographer Carl Hermann and the French mineralogist Charles-Victor Mauguin...

or international notation, often used in crystallography

Crystallography

Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...

. In the infinite limit, these groups become the one-dimensional line group

Line group

A line group is a mathematical way of describing symmetries associated with moving along a line. These symmetries include repeating along that line, making that line a one-dimensional lattice...

s.

If a group is a symmetry of a two-dimensional lattice

Lattice (group)

In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...

or grid, then the crystallographic restriction theorem

Crystallographic restriction theorem

The crystallographic restriction theorem in its basic form was based on the observation that the rotational symmetries of a crystal are usually limited to 2-fold, 3-fold, 4-fold, and 6-fold...

restricts the value of n to 1, 2, 3, 4, and 6 for both families. There are thus 10 two-dimensional crystallographic point group

Crystallographic point group

In crystallography, a crystallographic point group is a set of symmetry operations, like rotations or reflections, that leave a central point fixed while moving other directions and faces of the crystal to the positions of features of the same kind...

s:

C₁, C₂, C₃, C₄, C₆, D₁, D₂, D₃, D₄, D₆

The groups may be constructed as follows:

C_n. Generated by an element also called C_n, which corresponds to a rotation by angle 2π/n. Its elements are E (the identity), C_n, C_n², ..., C_n^n-1, corresponding to rotation angles 0, 2π/n, 4π/n, ..., 2(n-1)π/n.
D_n. Generated by element C_n and reflection σ. Its elements are the elements of group C_n, with elements σ, C_nσ, C_n²σ, ..., C_n^n-1σ added. These additional ones correspond to reflections across lines with orientation angles 0, π/n, 2π/n, ..., (n-1)π/n. D_n is thus a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...

of C_n and the group (E,σ).

All of these groups have distinct abstract groups, except for C₂ and D₁, which share abstract group Z₂. All of the cyclic groups are abelian or commutative, but only two of the dihedral groups are: D₁ ~ Z₂ and D₂ ~ Z₂×Z₂. In fact, D₃ is the smallest nonabelian group.

For n even, the Hermann-Mauguin symbol nm is an abbreviation for the full symbol nmm, as explained below. The n in the H-M symbol denotes n-fold rotations, while the m denotes reflection or mirror planes.

Parity of n	Full Intl	Reflection lines for regular polygon
Even n	nmm	vertex to vertex, edge center to edge center (2 families, 2 m's)
Odd n	nm	vertex to edge center (1 family, 1 m)

More general groups

These groups are readily constructed with two-dimensional orthogonal matrices

Orthogonal matrix

In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....

.

The continuous cyclic group SO(2) or C_∞ and its subgroups have elements that are rotation matrices:

where SO(2) has any possible θ. Not surprisingly, SO(2) and its subgroups are all abelian; addition of rotation angles commutes.

For discrete cyclic groups C_n, elements C_n^k = R(2πk/n)

The continuous dihedral group O(2) or D_∞ and its subgroups with reflections have elements that include not only rotation matrices, but also reflection matrices:

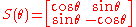
where O(2) has any possible θ. However, the only abelian subgroups of O(2) with reflections are D₁ and D₂.

For discrete dihedral groups D_n, elements C_n^kσ = S(2πk/n)

When one uses polar coordinates, the relationship of these groups to one-dimensional symmetry groups becomes evident.

Types of subgroups of SO(2):

finite cyclic
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...

subgroups C_n (n ≥ 1); for every n there is one isometry group, of abstract group type Z_n
finitely generated groups
Finitely generated abelian group
In abstract algebra, an abelian group is called finitely generated if there exist finitely many elements x1,...,xs in G such that every x in G can be written in the formwith integers n1,...,ns...

, each isomorphic to one of the form Z^m Z_n generated by C_n and m independent rotations with an irrational number of turns, and m, n ≥ 1; for each pair (m, n) there are uncountably many isometry groups, all the same as abstract group; for the pair (1, 1) the group is cyclic.
other countable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...

subgroups. For example, for an integer n, the group generated by all rotations of a number of turns equal to a negative integer power of n
uncountable subgroups, including SO(2) itself

For every subgroup of SO(2) there is a corresponding uncountable class of subgroups of O(2) that are mutually isomorphic as abstract group: each of the subgroups in one class is generated by the first-mentioned subgroup and a single reflection in a line through the origin. These are the (generalized) dihedral group

Dihedral group

In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...

s, including the finite ones D_n (n ≥ 1) of abstract group type Dih_n. For n = 1 the common notation is C_s, of abstract group type Z₂.

As topological subgroups

Topological group

In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...

of O(2), only the finite isometry groups and SO(2) and O(2) are closed.

These groups fall into two distinct families, according to whether they consist of rotation

Rotation

A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...

s only, or include reflection

Reflection (mathematics)

In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...

s. The cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...

s, C_n (abstract group type Z_n), consist of rotations by 360°/n, and all integer multiples. For example, a four legged stool has symmetry group

Symmetry group

The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...

C₄, consisting of rotations by 0°, 90°, 180°, and 270°. The symmetry group of a square

Square (geometry)

In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...

belongs to the family of dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...

s, D_n (abstract group type Dih_n), including as many reflections as rotations. The infinite rotational symmetry of the circle implies reflection symmetry as well, but formally the circle group S₁ is distinct from Dih(S₁) because the latter explicitly includes the reflections.

An infinite group need not be continuous; for example, we have a group of all integer multiples of rotation by 360°/√2, which does not include rotation by 180°. Depending on its application, homogeneity

Homogeneity (physics)

In general, homogeneity is defined as the quality or state of being homogeneous . For instance, a uniform electric field would be compatible with homogeneity...

up to an arbitrarily fine level of detail in a transverse direction may be considered equivalent to full homogeneity in that direction, in which case these symmetry groups can be ignored.

C_n and D_n for n = 1, 2, 3, 4, and 6 can be combined with translational symmetry, sometimes in more than one way. Thus these 10 groups give rise to 17 wallpaper group

Wallpaper group

A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...

Symmetry groups

The 2D symmetry groups correspond to the isometry groups, except that symmetry

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

according to O(2) and SO(2) can only be distinguished in the generalized symmetry concept applicable for vector field

Vector field

In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...

s.

Also, depending on application, homogeneity

Homogeneity (physics)

In general, homogeneity is defined as the quality or state of being homogeneous . For instance, a uniform electric field would be compatible with homogeneity...

up to arbitrarily fine detail in transverse direction may be considered equivalent to full homogeneity in that direction. This greatly simplifies the categorization: we can restrict ourselves to the closed topological subgroups of O(2): the finite ones and O(2) (circular symmetry

Circular symmetry

Circular symmetry in mathematical physics applies to a 2-dimensional field which can be expressed as a function of distance from a central point only. This means that all points on each circle take the same value....

), and for vector fields SO(2).

These groups also correspond to the one-dimensional symmetry groups, when wrapped around in a circle.

Combinations with translational symmetry

E(2) is a semidirect product

Semidirect product

In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...

of O(2) and the translation group T. In other words O(2) is a subgroup

Subgroup

In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...

of E(2) isomorphic to the quotient group

Quotient group

In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...

of E(2) by T:

O(2)

E(2) / T

There is a "natural" surjective group homomorphism

Group homomorphism

In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...

p : E(2) → E(2)/ T, sending each element g of E(2) to the coset of T to which g belongs, that is: p (g) = gT, sometimes called the canonical projection of E(2) onto E(2) / T or O(2). Its kernel

Kernel (algebra)

In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...

is T.

For every subgroup of E(2) we can consider its image under p: a point group consisting of the cosets to which the elements of the subgroup belong, in other words, the point group obtained by ignoring translational parts of isometries. For every discrete subgroup of E(2), due to the crystallographic restriction theorem

Crystallographic restriction theorem

The crystallographic restriction theorem in its basic form was based on the observation that the rotational symmetries of a crystal are usually limited to 2-fold, 3-fold, 4-fold, and 6-fold...

, this point group is either C_n or of type D_n for n = 1, 2, 3, 4, or 6.

C_n and D_n for n = 1, 2, 3, 4, and 6 can be combined with translational symmetry, sometimes in more than one way. Thus these 10 groups give rise to 17 wallpaper group

Wallpaper group

s, and the four groups with n = 1 and 2, give also rise to 7 frieze group

Frieze group

A frieze group is a mathematical concept to classify designs on two-dimensional surfaces which are repetitive in one direction, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...

s.

For each of the wallpaper groups p1, p2, p3, p4, p6, the image under p of all isometry groups (i.e. the "projections" onto E(2) / T or O(2) ) are all equal to the corresponding C_n; also two frieze groups correspond to C₁ and C₂.

The isometry groups of p6m are each mapped to one of the point groups of type D₆. For the other 11 wallpaper groups, each isometry group is mapped to one of the point groups of the types D₁, D₂, D₃, or D₄. Also five frieze groups correspond to D₁ and D₂.

For a given hexagonal translation lattice there are two different groups D₃, giving rise to P31m and p3m1. For each of the types D₁, D₂, and D₄ the distinction between the 3, 4, and 2 wallpaper groups, respectively, is determined by the translation vector associated with each reflection in the group: since isometries are in the same coset regardless of translational components, a reflection and a glide reflection

Glide reflection

In geometry, a glide reflection is a type of isometry of the Euclidean plane: the combination of a reflection in a line and a translation along that line. Reversing the order of combining gives the same result...

with the same mirror are in the same coset. Thus, isometry groups of e.g. type p4m and p4g are both mapped to point groups of type D₄.

For a given isometry group, the conjugates of a translation in the group by the elements of the group generate a translation group (a lattice

Lattice (group)

)—that is a subgroup of the isometry group that only depends on the translation we started with, and the point group associated with the isometry group. This is because the conjugate of the translation by a glide reflection is the same as by the corresponding reflection: the translation vector is reflected.

If the isometry group contains an n-fold rotation then the lattice has n-fold symmetry for even n and 2n-fold for odd n. If, in the case of a discrete isometry group containing a translation, we apply this for a translation of minimum length, then, considering the vector difference of translations in two adjacent directions, it follows that n ≤ 6, and for odd n that 2n ≤ 6, hence n = 1, 2, 3, 4, or 6 (the crystallographic restriction theorem

Crystallographic restriction theorem

The crystallographic restriction theorem in its basic form was based on the observation that the rotational symmetries of a crystal are usually limited to 2-fold, 3-fold, 4-fold, and 6-fold...

External links

http://www.math.ttu.edu/~drager/Classes/10MathCamp/handouts04.pdf, Geometric Transformations and Wallpaper Groups: Symmetries of Geometric Patterns (Discrete Groups of Isometries), by Lance Drager.
http://www.stanford.edu/~yishuwei/crystal.pdf Point Groups and Crystal Systems, by Yi-Shu Wei, pp. 4-5
The Geometry Center: 2.1 Formulas for Symmetries in Cartesian Coordinates (two dimensions)

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.