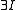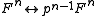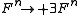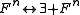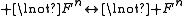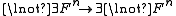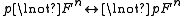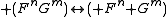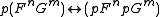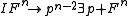Predicate functor logic
Encyclopedia
In mathematical logic
, predicate functor logic (PFL) is one of several ways to express first-order logic
(also known as predicate logic
) by purely algebraic means, i.e., without quantified variable
s. PFL employs a small number of algebraic devices called predicate functors (or predicate modifiers) that operate on terms to yield terms. PFL is mostly the invention of the logic
ian and philosopher Willard Quine.
in a manner analogous to how Boolean algebra algebraizes propositional logic. He designed PFL to have exactly the expressive power of first-order logic
with identity
. Hence the metamathematics
of PFL are exactly those of first-order logic with no interpreted predicate letters: both logics are sound
, complete, and undecidable
. Most work Quine published on logic and mathematics in the last 30 years of his life touched on PFL in some way.
Quine took "functor" from the writings of his friend Rudolf Carnap
, the first to employ it in philosophy
and mathematical logic
, and defined it as follows:
Ways other than PFL to algebraize first-order logic
include:
PFL is arguably the simplest of these formalisms, yet also the one about which the least has been written.
Quine had a lifelong fascination with combinatory logic
, attested to by his (1976) and his introduction to the translation in Van Heijenoort (1967) of the paper by the Russian logician Moses Schönfinkel
founding combinatory logic. When Quine began working on PFL in earnest, in 1959, combinatory logic was commonly deemed a failure for the following reasons:
, primitives, and axioms described in this section are largely Kuhn's (1983). The semantics
of the functors are Quine's (1982). The rest of this entry incorporates some terminology from Bacon (1985).
The "combinatory" (the word is Quine's) predicate functors, all monadic and peculiar to PFL, are Inv, inv, ∃, +, and p. A term is either an atomic term, or constructed by the following recursive rule. If τ is a term, then Invτ, invτ, ∃τ, +τ, and pτ are terms. A functor with a superscript n, n a natural number
> 1, denotes n consecutive applications (iterations) of that functor.
A formula is either a term or defined by the recursive rule: if α and β are formulas, then αβ and ~(α) are likewise formulas. Hence "~" is another monadic functor, and concatenation is the sole dyadic predicate functor. Quine called these functors "alethic." The natural interpretation of "~" is negation
; that of concatenation is any connective
that, when combined with negation, forms a functionally complete set of connectives. Quine's preferred functionally complete set was conjunction
and negation
. Thus concatenated terms are taken as conjoined. The notation + is Bacon's (1985); all other notation is Quine's (1976; 1982). The alethic part of PFL is identical to the Boolean term schemata of Quine (1982).
As is well known, the two alethic functors could be replaced by a single dyadic functor with the following syntax
and semantics
: if α and β are formulas, then (αβ) is a formula whose semantics are "not (α and/or β)" (see NAND
and NOR
).
and complete.
This section is built around the primitive predicate functors and a few defined ones. The alethic functors can be axiomatized by any set of axioms for sentential logic whose primitives are negation and one of ∧ or ∨. Equivalently, all tautologies
of sentential logic can be taken as axioms.
Quine's (1982) semantics for each predicate functor are stated below in terms of abstraction
(set builder notation), followed by either the relevant axiom from Kuhn (1983), or a definition from Quine (1976). The notation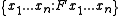 denotes the set of n-tuples satisfying the atomic formula
denotes the set of n-tuples satisfying the atomic formula 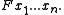
Identity is reflexive
(Ixx), symmetric (Ixy→Iyx), transitive ( (Ixy∧Iyz) → Ixz), and obeys the substitution property: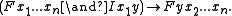
Cropping enables two useful defined functors:
S generalizes the notion of reflexivity to all terms of any finite degree greater than 2. N.B: S should not be confused with the primitive combinator
S of combinatory logic.
Here only, Quine adopted an infix notation, because this infix notation for Cartesian product is very well established in mathematics. Cartesian product allows restating conjunction as follows: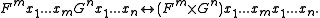
Reorder the concatenated argument list so as to shift a pair of duplicate variables to the far left, then invoke S to eliminate the duplication. Repeating this as many times as required results in an argument list of length max{m,n).
The next three functors enable reordering argument lists at will.
Given an argument list consisting of n variables, p implicitly treats the last n-1 variables like a bicycle chain, with each variable constituting a link in the chain. One application of p advances the chain by one link. k consecutive applications of p to Fn moves the k+1 variable to the second argument position in F.
When n=2, Inv and inv merely interchange x1 and x2. When n=1, they have no effect. Hence p has no effect when n<3.
Kuhn (1983) takes Major inversion and Minor inversion as primitive. The notation p in Kuhn corresponds to inv; he has no analog to Permutation and hence has no axioms for it. If, following Quine (1976), p is taken as primitive, Inv and inv can be defined as nontrivial combinations of +, ∃, and iterated p.
The following table summarizes how the functors affect the degrees of their arguments.
are:
n-1 consecutive iterations of p restores the status quo ante:
+ and ∃ annihilate each other:
Negation distributes over +, ∃, and p:
+ and p distributes over conjunction:
Identity has the interesting implication:
Quine also conjectured the rule: If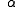 is a PFL theorem, then so are
is a PFL theorem, then so are 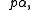
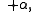 and
and 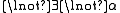 .
.
, negation
, Identity, Padding, and Major and Minor inversion as primitive, and Cropping as defined. Employing terminology and notation differing somewhat from the above, Bacon (1985) sets out two formulations of PFL:
Bacon also:
is adapted from Quine (1976: 300-2). Given a closed formula
of first-order logic
, first do the following:
Now apply the following algorithm to the preceding result:
1. Translate the matrices of the most deeply nested quantifiers into disjunctive normal form
, consisting of disjuncts of conjuncts of terms, negating atomic terms as required. The resulting subformula contains only negation, conjunction, disjunction, and existential quantification.
2. Distribute the existential quantifiers over the disjuncts in the matrix using the rule of passage
(Quine 1982: 119):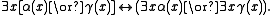
3. Replace conjunction by Cartesian product
, by invoking the fact: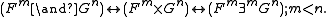
4. Concatenate the argument lists of all atomic terms, and move the concatenated list to the far right of the subformula.
5. Use Inv and inv to move all instances of the quantified variable (call it y) to the left of the argument list.
6. Invoke S as many times as required to eliminate all but the last instance of y. Eliminate y by prefixing the subformula with one instance of ∃.
7. Repeat (1)-(6) until all quantified variables have been eliminated. Eliminate any disjunctions falling within the scope of a quantifier by invoking the equivalence: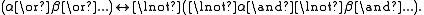
The reverse translation, from PFL to first-order logic, is discussed in Quine (1976: 302-4).
The canonical foundation of mathematics is axiomatic set theory, with a background logic consisting of first-order logic
with identity
, with a universe of discourse consisting entirely of sets. There is a single predicate letter
of degree 2, interpreted as set membership. The PFL translation of the canonical axiomatic set theory ZFC is not difficult, as no ZFC axiom requires more than 6 quantified variables.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, predicate functor logic (PFL) is one of several ways to express first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
(also known as predicate logic
Predicate logic
In mathematical logic, predicate logic is the generic term for symbolic formal systems like first-order logic, second-order logic, many-sorted logic or infinitary logic. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified...
) by purely algebraic means, i.e., without quantified variable
Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
s. PFL employs a small number of algebraic devices called predicate functors (or predicate modifiers) that operate on terms to yield terms. PFL is mostly the invention of the logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
ian and philosopher Willard Quine.
Motivation
The source for this section, as well as for much of this entry, is Quine (1976). Quine proposed PFL as a way of algebraizing first-order logicFirst-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
in a manner analogous to how Boolean algebra algebraizes propositional logic. He designed PFL to have exactly the expressive power of first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
with identity
Identity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
. Hence the metamathematics
Metamathematics
Metamathematics is the study of mathematics itself using mathematical methods. This study produces metatheories, which are mathematical theories about other mathematical theories...
of PFL are exactly those of first-order logic with no interpreted predicate letters: both logics are sound
Consistency proof
In logic, a consistent theory is one that does not contain a contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent if and only if it has a model, i.e. there exists an interpretation under which all...
, complete, and undecidable
Undecidable
Undecidable may refer to:In mathematics and logic* Undecidable problem - a decision problem which no algorithm can decide* "Undecidable" is sometimes used as a synonym of "independent", where a formula in mathematical logic is independent of a logical theory if neither that formula nor its negation...
. Most work Quine published on logic and mathematics in the last 30 years of his life touched on PFL in some way.
Quine took "functor" from the writings of his friend Rudolf Carnap
Rudolf Carnap
Rudolf Carnap was an influential German-born philosopher who was active in Europe before 1935 and in the United States thereafter. He was a major member of the Vienna Circle and an advocate of logical positivism....
, the first to employ it in philosophy
Philosophy
Philosophy is the study of general and fundamental problems, such as those connected with existence, knowledge, values, reason, mind, and language. Philosophy is distinguished from other ways of addressing such problems by its critical, generally systematic approach and its reliance on rational...
and mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, and defined it as follows:
"The word functor, grammatical in import but logical in habitat... is a sign that attaches to one or more expressions of given grammatical kind(s) to produce an expression of a given grammatical kind." (Quine 1982: 129)
Ways other than PFL to algebraize first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
include:
- Cylindric algebraCylindric algebraThe notion of cylindric algebra, invented by Alfred Tarski, arises naturally in the algebraization of first-order logic with equality. This is comparable to the role Boolean algebras play for propositional logic. Indeed, cylindric algebras are Boolean algebras equipped with additional...
by Alfred TarskiAlfred TarskiAlfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
and his American students. The simplified cylindric algebra proposed in Bernays (1959) led Quine to write the paper containing the first use of the phrase "predicate functor"; - The polyadic algebraPolyadic algebraPolyadic algebras are algebraic structures introduced by Paul Halmos. They are related to first-order logic in a way analogous to the relationship between Boolean algebras and propositional logic .There are other ways to relate first-order logic to algebra, including Tarski's cylindric algebras...
of Paul HalmosPaul HalmosPaul Richard Halmos was a Hungarian-born American mathematician who made fundamental advances in the areas of probability theory, statistics, operator theory, ergodic theory, and functional analysis . He was also recognized as a great mathematical expositor.-Career:Halmos obtained his B.A...
. By virtue of its economical primitives and axioms, this algebra most resembles PFL; - Relation algebraRelation algebraIn mathematics and abstract algebra, a relation algebra is a residuated Boolean algebra expanded with an involution called converse, a unary operation...
algebraizes the fragment of first-order logicFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
consisting of formulas having no atomic formula lying in the scope of more than three quantifiers. That fragment suffices, however, for Peano arithmetic and the axiomatic set theory ZFC; hence relation algebra, unlike PFL, is incompletable. Most work on relation algebra since about 1920 has been by Tarski and his American students. The power of relation algebra did not become manifest until the monograph Tarski and Givant (1987), published after the three important papers bearing on PFL, namely Bacon (1985), Kuhn (1983), and Quine (1976); - Combinatory logicCombinatory logicCombinatory logic is a notation introduced by Moses Schönfinkel and Haskell Curry to eliminate the need for variables in mathematical logic. It has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming...
builds on combinators, higher order functions whose domainDomain (mathematics)In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
is another combinator or function, and whose rangeRange (mathematics)In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
is yet another combinator. Hence combinatory logicCombinatory logicCombinatory logic is a notation introduced by Moses Schönfinkel and Haskell Curry to eliminate the need for variables in mathematical logic. It has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming...
goes beyond first-order logic by having the expressive power of set theorySet theorySet theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, which makes combinatory logic vulnerable to paradoxParadoxSimilar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
es. A predicate functor, on the other hand, simply maps predicates (also called termsTerm (mathematics)A term is a mathematical expression which may form a separable part of an equation, a series, or another expression.-Definition:In elementary mathematics, a term is either a single number or variable, or the product of several numbers or variables separated from another term by a + or - sign in an...
) into predicates.
PFL is arguably the simplest of these formalisms, yet also the one about which the least has been written.
Quine had a lifelong fascination with combinatory logic
Combinatory logic
Combinatory logic is a notation introduced by Moses Schönfinkel and Haskell Curry to eliminate the need for variables in mathematical logic. It has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming...
, attested to by his (1976) and his introduction to the translation in Van Heijenoort (1967) of the paper by the Russian logician Moses Schönfinkel
Moses Schönfinkel
Moses Ilyich Schönfinkel, also known as Moisei Isai'evich Sheinfinkel , was a Russian logician and mathematician, known for the invention of combinatory logic.- Life :Schönfinkel attended the Novorossiysk University of Odessa, studying mathematics under Samuil Osipovich...
founding combinatory logic. When Quine began working on PFL in earnest, in 1959, combinatory logic was commonly deemed a failure for the following reasons:
- Until Dana ScottDana ScottDana Stewart Scott is the emeritus Hillman University Professor of Computer Science, Philosophy, and Mathematical Logic at Carnegie Mellon University; he is now retired and lives in Berkeley, California...
began writing on the model theoryModel theoryIn mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
of combinatory logic in the late 1960s, nearly all work on that logic had been by Haskell CurryHaskell CurryHaskell Brooks Curry was an American mathematician and logician. Curry is best known for his work in combinatory logic; while the initial concept of combinatory logic was based on a single paper by Moses Schönfinkel, much of the development was done by Curry. Curry is also known for Curry's...
, his students, or by Robert FeysRobert FeysRobert Feys was a Belgian logician and philosopher, who worked at the University of Leuven .In 1958 Feys and Haskell B. Curry devised the type inference algorithm for the simply typed lambda calculus ....
in Belgium; - Satisfactory axiomatic formulations of combinatory logic were slow in coming. In the 1930s, some formulations of combinatory logic were found to be inconsistentConsistency proofIn logic, a consistent theory is one that does not contain a contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent if and only if it has a model, i.e. there exists an interpretation under which all...
. Curry also discovered the Curry paradox, peculiar to combinatory logic; - The lambda calculusLambda calculusIn mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
, with the same expressive power as combinatory logicCombinatory logicCombinatory logic is a notation introduced by Moses Schönfinkel and Haskell Curry to eliminate the need for variables in mathematical logic. It has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming...
, was seen as a superior formalism.
Kuhn's formalization
The PFL syntaxSyntax
In linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
, primitives, and axioms described in this section are largely Kuhn's (1983). The semantics
Semantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
of the functors are Quine's (1982). The rest of this entry incorporates some terminology from Bacon (1985).
Syntax
An atomic term is an upper case Latin letter, I and S excepted, followed by a numerical superscript called its degree, or by concatenated lower case variables, collectively known as an argument list. The degree of a term conveys the same information as the number of variables following a predicate letter. An atomic term of degree 0 denotes a Boolean variable or a truth value. The degree of I is invariably 2 and so is not indicated.The "combinatory" (the word is Quine's) predicate functors, all monadic and peculiar to PFL, are Inv, inv, ∃, +, and p. A term is either an atomic term, or constructed by the following recursive rule. If τ is a term, then Invτ, invτ, ∃τ, +τ, and pτ are terms. A functor with a superscript n, n a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
> 1, denotes n consecutive applications (iterations) of that functor.
A formula is either a term or defined by the recursive rule: if α and β are formulas, then αβ and ~(α) are likewise formulas. Hence "~" is another monadic functor, and concatenation is the sole dyadic predicate functor. Quine called these functors "alethic." The natural interpretation of "~" is negation
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
; that of concatenation is any connective
Connective
Connective may be referring to:* Bains::connective* Logical connective* Connective tissue* Discourse connective, in linguistics, a word or phrase like "therefore" or "in other words"....
that, when combined with negation, forms a functionally complete set of connectives. Quine's preferred functionally complete set was conjunction
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
and negation
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
. Thus concatenated terms are taken as conjoined. The notation + is Bacon's (1985); all other notation is Quine's (1976; 1982). The alethic part of PFL is identical to the Boolean term schemata of Quine (1982).
As is well known, the two alethic functors could be replaced by a single dyadic functor with the following syntax
Syntax
In linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
and semantics
Semantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
: if α and β are formulas, then (αβ) is a formula whose semantics are "not (α and/or β)" (see NAND
Nand
NAND may stand for:*Nand , an Indian classical raga.*Logical NAND , a binary operation in logic.**NAND gate, an electronic gate that implements a logical NAND....
and NOR
Nor
Nor may refer to:*In grammar, nor is a coordinating conjunction*Nór, the eponymous founder-king of Norway in Norse mythology*Nor , a character in the book in Wicked...
).
Axioms and semantics
Quine set out neither axiomatization nor proof procedure for PFL. The following axiomatization of PFL, one of two proposed in Kuhn (1983), is concise and easy to describe, but makes extensive use of free variables and so does not do full justice to the spirit of PFL. Kuhn gives another axiomatization dispensing with free variables, but that is harder to describe and that makes extensive use of defined functors. Kuhn proved both of his PFL axiomatizations soundConsistency proof
In logic, a consistent theory is one that does not contain a contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent if and only if it has a model, i.e. there exists an interpretation under which all...
and complete.
This section is built around the primitive predicate functors and a few defined ones. The alethic functors can be axiomatized by any set of axioms for sentential logic whose primitives are negation and one of ∧ or ∨. Equivalently, all tautologies
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
of sentential logic can be taken as axioms.
Quine's (1982) semantics for each predicate functor are stated below in terms of abstraction
Abstraction
Abstraction is a process by which higher concepts are derived from the usage and classification of literal concepts, first principles, or other methods....
(set builder notation), followed by either the relevant axiom from Kuhn (1983), or a definition from Quine (1976). The notation
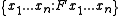 denotes the set of n-tuples satisfying the atomic formula
denotes the set of n-tuples satisfying the atomic formula 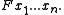
- Identity, I, is defined as:
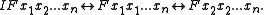
Identity is reflexive
Reflexive
Reflexive may refer to:In fiction:*MetafictionIn grammar:*Reflexive pronoun, a pronoun with a reflexive relationship with its self-identical antecedent*Reflexive verb, where a semantic agent and patient are the same...
(Ixx), symmetric (Ixy→Iyx), transitive ( (Ixy∧Iyz) → Ixz), and obeys the substitution property:
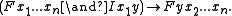
- Padding, +, adds a variable to the left of any argument list.
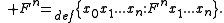
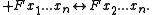
- Cropping, ∃, erases the leftmost variable in any argument list.
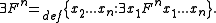
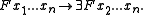
Cropping enables two useful defined functors:
- Reflection, S:
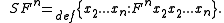
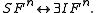
S generalizes the notion of reflexivity to all terms of any finite degree greater than 2. N.B: S should not be confused with the primitive combinator
Combinatory logic
Combinatory logic is a notation introduced by Moses Schönfinkel and Haskell Curry to eliminate the need for variables in mathematical logic. It has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming...
S of combinatory logic.
- Cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
, ;
;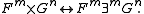
Here only, Quine adopted an infix notation, because this infix notation for Cartesian product is very well established in mathematics. Cartesian product allows restating conjunction as follows:
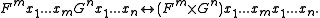
Reorder the concatenated argument list so as to shift a pair of duplicate variables to the far left, then invoke S to eliminate the duplication. Repeating this as many times as required results in an argument list of length max{m,n).
The next three functors enable reordering argument lists at will.
- Major inversion, Inv, rotates the variables in an argument list to the right, so that the last variable becomes the first.
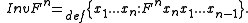
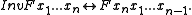
- Minor inversion, inv, swaps the first two variables in an argument list.
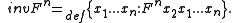
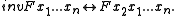
- Permutation, p, rotates the second through last variables in an argument list to the left, so that the second variable becomes the last.
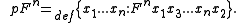
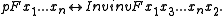
Given an argument list consisting of n variables, p implicitly treats the last n-1 variables like a bicycle chain, with each variable constituting a link in the chain. One application of p advances the chain by one link. k consecutive applications of p to Fn moves the k+1 variable to the second argument position in F.
When n=2, Inv and inv merely interchange x1 and x2. When n=1, they have no effect. Hence p has no effect when n<3.
Kuhn (1983) takes Major inversion and Minor inversion as primitive. The notation p in Kuhn corresponds to inv; he has no analog to Permutation and hence has no axioms for it. If, following Quine (1976), p is taken as primitive, Inv and inv can be defined as nontrivial combinations of +, ∃, and iterated p.
The following table summarizes how the functors affect the degrees of their arguments.
| Expression | Degree |
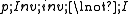 |
no change |
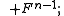 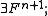 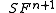 |
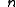 |
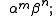 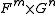 |
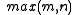 |
Rules
All instances of a predicate letter may be replaced by another predicate letter of the same degree, without affecting validity. The rulesFirst-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
are:
- Modus ponensModus ponensIn classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
; - Let α and β be PFL formulas in which
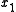 does not appear. Then if
does not appear. Then if 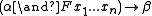 is a PFL theorem, then
is a PFL theorem, then 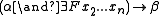 is likewise a PFL theorem.
is likewise a PFL theorem.
Some useful results
Instead of axiomatizing PFL, Quine (1976) proposed the following conjectures as candidate axioms.n-1 consecutive iterations of p restores the status quo ante:
+ and ∃ annihilate each other:
Negation distributes over +, ∃, and p:
+ and p distributes over conjunction:
Identity has the interesting implication:
Quine also conjectured the rule: If
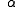 is a PFL theorem, then so are
is a PFL theorem, then so are 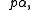
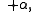 and
and 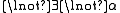 .
.Bacon's work
Bacon (1985) takes the conditionalConditional
Conditional may refer to:*Causal conditional, if X then Y, where X is a cause of Y*Conditional mood , a verb form in many languages*Conditional probability, the probability of an event A given that another event B has occurred...
, negation
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
, Identity, Padding, and Major and Minor inversion as primitive, and Cropping as defined. Employing terminology and notation differing somewhat from the above, Bacon (1985) sets out two formulations of PFL:
- A natural deductionNatural deductionIn logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...
formulation in the style of Frederick Fitch. Bacon proves this formulation soundConsistency proofIn logic, a consistent theory is one that does not contain a contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent if and only if it has a model, i.e. there exists an interpretation under which all...
and complete in full detail. - An axiomatic formulation which Bacon asserts, but does not prove, equivalent to the preceding one. Some of these axioms are simply Quine conjectures restated in Bacon's notation.
Bacon also:
- Discusses the relation of PFL to the term logicTerm logicIn philosophy, term logic, also known as traditional logic or aristotelian logic, is a loose name for the way of doing logic that began with Aristotle and that was dominant until the advent of modern predicate logic in the late nineteenth century...
of Sommers (1982), and argues that recasting PFL using a syntax proposed in Lockwood's appendix to Sommers, should make PFL easier to "read, use, and teach"; - Touches on the group theoreticGroup theoryIn mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
structure of Inv and inv; - Mentions that sentential logic, monadic predicate logic, the modal logicModal logicModal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
S5S5 (modal logic)In logic and philosophy, S5 is one of five systems of modal logic proposed byClarence Irving Lewis and Cooper Harold Langford in their 1932 book Symbolic Logic.It is a normal modal logic, and one of the oldest systems of modal logic of any kind....
, and the Boolean logic of (un)permuted relationRelation (mathematics)In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
s, are all fragments of PFL.
From first-order logic to PFL
The following algorithmAlgorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
is adapted from Quine (1976: 300-2). Given a closed formula
Sentence (mathematical logic)
In mathematical logic, a sentence of a predicate logic is a boolean-valued well formed formula with no free variables. A sentence can be viewed as expressing a proposition, something that may be true or false...
of first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, first do the following:
- Attach a numerical subscript to every predicate letter, stating its degree;
- Translate all universal quantifiers into existential quantifiers and negation;
- Restate all atomic formulaAtomic formulaIn mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...
s of the form x=y as Ixy.
Now apply the following algorithm to the preceding result:
1. Translate the matrices of the most deeply nested quantifiers into disjunctive normal form
Disjunctive normal form
In boolean logic, a disjunctive normal form is a standardization of a logical formula which is a disjunction of conjunctive clauses. As a normal form, it is useful in automated theorem proving. A logical formula is considered to be in DNF if and only if it is a disjunction of one or more...
, consisting of disjuncts of conjuncts of terms, negating atomic terms as required. The resulting subformula contains only negation, conjunction, disjunction, and existential quantification.
2. Distribute the existential quantifiers over the disjuncts in the matrix using the rule of passage
Rules of passage (logic)
In mathematical logic, the rules of passage govern how quantifiers distribute over the basic logical connectives of first-order logic. The rules of passage govern the "passage" from any formula of first-order logic to the equivalent formula in prenex normal form, and vice versa.-The rules:See...
(Quine 1982: 119):
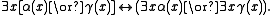
3. Replace conjunction by Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
, by invoking the fact:
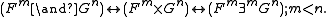
4. Concatenate the argument lists of all atomic terms, and move the concatenated list to the far right of the subformula.
5. Use Inv and inv to move all instances of the quantified variable (call it y) to the left of the argument list.
6. Invoke S as many times as required to eliminate all but the last instance of y. Eliminate y by prefixing the subformula with one instance of ∃.
7. Repeat (1)-(6) until all quantified variables have been eliminated. Eliminate any disjunctions falling within the scope of a quantifier by invoking the equivalence:
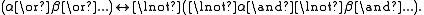
The reverse translation, from PFL to first-order logic, is discussed in Quine (1976: 302-4).
The canonical foundation of mathematics is axiomatic set theory, with a background logic consisting of first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
with identity
Identity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
, with a universe of discourse consisting entirely of sets. There is a single predicate letter
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
of degree 2, interpreted as set membership. The PFL translation of the canonical axiomatic set theory ZFC is not difficult, as no ZFC axiom requires more than 6 quantified variables.
See also
- algebraic logicAlgebraic logicIn mathematical logic, algebraic logic is the study of logic presented in an algebraic style.What is now usually called classical algebraic logic focuses on the identification and algebraic description of models appropriate for the study of various logics and connected problems...
- combinatory logicCombinatory logicCombinatory logic is a notation introduced by Moses Schönfinkel and Haskell Curry to eliminate the need for variables in mathematical logic. It has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming...
- cylindric algebraCylindric algebraThe notion of cylindric algebra, invented by Alfred Tarski, arises naturally in the algebraization of first-order logic with equality. This is comparable to the role Boolean algebras play for propositional logic. Indeed, cylindric algebras are Boolean algebras equipped with additional...
- relation algebraRelation algebraIn mathematics and abstract algebra, a relation algebra is a residuated Boolean algebra expanded with an involution called converse, a unary operation...
- term logicTerm logicIn philosophy, term logic, also known as traditional logic or aristotelian logic, is a loose name for the way of doing logic that began with Aristotle and that was dominant until the advent of modern predicate logic in the late nineteenth century...