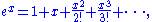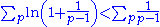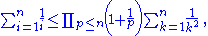Proof that the sum of the reciprocals of the primes diverges
Encyclopedia
The sum of the reciprocal
s of all prime number
s diverges, that is:

This was proved by Leonhard Euler
in 1737, and strengthens Euclid
's 3rd-century-BC result that there are infinitely many prime number
s.
There is a variety of proofs of Euler's result, including a lower bound for the partial sums stating that
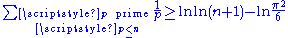
for all natural numbers n. The iterated natural logarithm
indicates that the divergence might be very slow, which is indeed the case, see Meissel–Mertens constant.
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
s of all prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s diverges, that is:

This was proved by Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
in 1737, and strengthens Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
's 3rd-century-BC result that there are infinitely many prime number
Euclid's theorem
Euclid's theorem is a fundamental statement in number theory that asserts that there are infinitely many prime numbers. There are several well-known proofs of the theorem.-Euclid's proof:...
s.
There is a variety of proofs of Euler's result, including a lower bound for the partial sums stating that
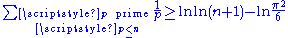
for all natural numbers n. The iterated natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
indicates that the divergence might be very slow, which is indeed the case, see Meissel–Mertens constant.
The harmonic series
First, we describe how Euler originally discovered the result. He was considering the harmonic seriesHarmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
-
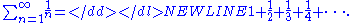
He had already used the following "product formula" to show the existence of infinitely many primes.
-

(Here, the product is taken over all primes p; in the following, a sum or product taken over p always represents a sum or product taken over a specified set of primes, unless noted otherwise.)
Such infinite products are today called Euler productEuler productIn number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The name arose from the case of the Riemann zeta-function, where such a product representation was proved by Leonhard Euler.-Definition:...
s. The product above is a reflection of the fundamental theorem of arithmeticFundamental theorem of arithmeticIn number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
. (Multiply out the right side as you would like to do.) Of course, the above "equation" is not necessary because the harmonic series is known (by other means) to diverge. This type of formal manipulation was common at the time, when mathematicians were still experimenting with the new tools of calculusCalculusCalculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
.
Euler noted that if there were only a finite number of primes, then the product on the right would clearly converge, contradicting the divergence of the harmonic series. (In modern language, we now say that the existence of infinitely many primes is reflected by the fact that the Riemann zeta function has a simple pole at s = 1.)
First proof
Euler took the above product formula and proceeded to make a sequence of audacious leaps of logic. First, he took the natural logarithm of each side, then he used the Taylor series expansion for ln(1 − x) as well as the sum of a geometric series:
-
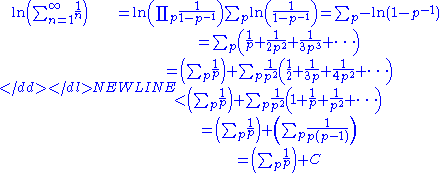
for a fixed constant C < 1. Since the sum of the reciprocals of the first n positive integers is asymptotic to ln(n), (i.e. their ratio approaches one as n approaches infinity), Euler then concluded
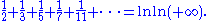
It is almost certain that Euler meant that the sum of the reciprocals of the primes less than n is asymptotic to ln(ln(n)) as n approaches infinity. It turns out this is indeed the case; Euler had reached a correct result by questionable means.
Simpler version of the above proof
-

Since
we get ex > 1 + x and x > ln(1 + x).
So
Hence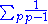 diverges. But 1/(pi − 1) < 1/pi−1 where pi is the ith prime. Hence
diverges. But 1/(pi − 1) < 1/pi−1 where pi is the ith prime. Hence 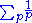 diverges.
diverges.
Second proof
The following proof by contradiction is due to Paul ErdősPaul ErdosPaul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
.
Let pi denote the ith prime number. Assume that the sumSeries (mathematics)A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
of the reciprocals of the primes converges, i.e.
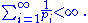
Then there exists a positive integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
k such that
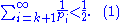
For a positive integer x let Mx denote the set of those n in {1, 2, . . ., x} which are not divisible by any prime greater than pk. We will now derive an upper and a lower estimate for the number |Mx| of elements in Mx. For large x, these bounds will turn out to be contradictory.
Upper estimate:
Every n in Mx can be written as n = r m2 with positive integers m and r, where r is square-freeSquare-free integerIn mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
. Since only the k primes p1 . . ., pk can show up (with exponent 1) in the prime factorizationFundamental theorem of arithmeticIn number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
of r, there are at most 2k different possibilities for r. Furthermore, there are at most √x possible values for m. This gives us the upper estimate

Lower estimate:
The remaining x − |Mx| numbers in the set difference {1, 2, . . ., x} \ Mx are all divisible by a prime greater than pk. Let Ni,x denote the set of those n in {1, 2, . . ., x} which are divisible by the ith prime pi. Then

Since the number of integers in Ni,x is at most x/pi (actually zero for pi > x), we get
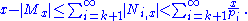
Using (1), this implies
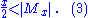
Contradiction:
For every integer x ≥ 22k + 2, the estimates (2) and (3) cannot hold simultaneously.
Third proof
Here is another proof that actually gives a lower estimate for the partial sums; in particular, it shows that these sums grow at least as fast as ln(ln(n)). The proof is an adaptation of the product expansion idea of Euler. In the following, a sum or product taken over p always represents a sum or product taken over a specified set of primes.
The proof rests upon the following four inequalities:
- Every positive integer i can be uniquely expressed as the product of a square-free integer and a square. This gives the inequality
-
- where for every i between 1 and n the (expanded) product contains to the square-free part of i and the sum contains to the square part of i (see fundamental theorem of arithmeticFundamental theorem of arithmeticIn number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
).
- The upper estimate for the natural logarithmNatural logarithmThe natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
-

- The lower estimate 1 + x < exp(x) for the exponential functionExponential functionIn mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
, which holds for all x > 0.
- Let n ≥ 2. The upper bound (using a telescoping sum) for the partial sums (convergence is all we really need)
-

Combining all these inequalities, we see that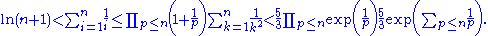
Dividing through by 5/3 and taking the natural logarithm of both sides gives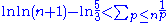
as desired. ∎Q.E.D.Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...
Using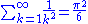
(see Basel problemBasel problemThe Basel problem is a famous problem in mathematical analysis with relevance to number theory, first posed by Pietro Mengoli in 1644 and solved by Leonhard Euler in 1735. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate...
), the above constant ln (5/3) = 0.51082... can be improved to ln(π2/6) = 0.4977...; in fact it turns out that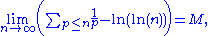
where M = 0.261497... is the Meissel–Mertens constant (somewhat analogous to the much more famous Euler–Mascheroni constantEuler–Mascheroni constantThe Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
).
Fourth proof
From Dusart's inequality (see PNT), we get

Then
by the integral test for convergenceIntegral test for convergenceIn mathematics, the integral test for convergence is a method used to test infinite series of non-negative terms for convergence. An early form of the test of convergence was developed in India by Madhava in the 14th century, and by his followers at the Kerala School...
. This shows that the series on the left diverges.
See also
- Euclid's theoremEuclid's theoremEuclid's theorem is a fundamental statement in number theory that asserts that there are infinitely many prime numbers. There are several well-known proofs of the theorem.-Euclid's proof:...
that there are infinitely many primes - Small set (combinatorics)
- Brun's theoremBrun's theoremIn number theory, Brun's theorem was proved by Viggo Brun in 1919. It states that the sum of the reciprocals of the twin primes is convergent with a finite value known as Brun's constant, usually denoted by B2...
External links
- Euclid's theorem
- The lower estimate 1 + x < exp(x) for the exponential function
-
-
-
-