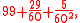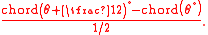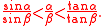Ptolemy's table of chords
Encyclopedia
The table of chords, created by the astronomer and geometer Ptolemy
in Egypt
during the 2nd century AD, is a trigonometric table in Book I, chapter 11 of Ptolemy's Almagest
, a treatise on mathematical astronomy. It is essentially equivalent to a table of values of the sine
function. It was the earliest trigonometric table extensive enough for many practical purposes, including those of astronomy (an earlier table of chords by Hipparchus
gave chords only for arcs that were multiples of 7½° = π/24 radians). Several centuries passed before more extensive trigonometric tables were created.
of a circle
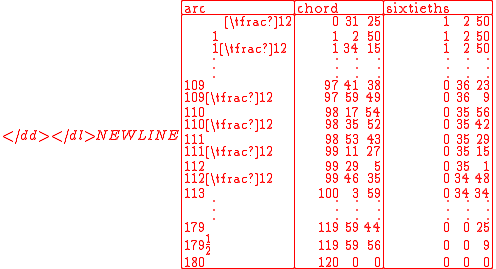
is a line segment whose endpoints are on the circle. Ptolemy considered a circle of diameter 120. He tabulated the length of a chord whose endpoints are separated by an arc of n degrees, for n ranging from 1/2 to 180 by increments of 1/2. In modern notation, the length of the chord corresponding to an arc of θ degrees is
As θ goes from 0 to 180, the chord of a θ° arc goes from 0 to 120. For tiny arcs, the chord is to the arc as π is to 3, or more precisely, the ratio can be made as close as desired to π/3 ≈ 1.04719755 by making θ small enough. Thus, for the arc of (1/2)°, the chord is slightly more than the arc. As the arc increases, the ratio of the chord to the arc decreases. When the arc reaches 60°, the chord is exactly equal to the arc, i.e. chord 60° = 60. For arcs of more than 60°, the chord is less than the arc, until an arc of 180° is reached, when the chord is only 120.
The fractional parts of chord lengths were expressed in sexagesimal, i.e. base-60, numerals. For example, where the length of a chord subtended by a 112° arc is reported to be "99 29 5", that means that its length is
rounded to the nearest 1/602.
After the columns for the arc and the chord, a third column is labeled "sixtieths". For an arc of θ°, the entry in the "sixtieths" column is
This is the average number of sixtieths that must be added to chord(θ°) for each 1° increase in θ°, between the entry for θ° and that for (θ + ½)°. Thus, it is used for linear interpolation
. Glowatzki and Göttsche showed that Ptolemy must have calculated chords to five sexigesimal places in order to achieve the degree of accuracy found in the "sixtieths" column.
Ptolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
in Egypt
Egypt
Egypt , officially the Arab Republic of Egypt, Arabic: , is a country mainly in North Africa, with the Sinai Peninsula forming a land bridge in Southwest Asia. Egypt is thus a transcontinental country, and a major power in Africa, the Mediterranean Basin, the Middle East and the Muslim world...
during the 2nd century AD, is a trigonometric table in Book I, chapter 11 of Ptolemy's Almagest
Almagest
The Almagest is a 2nd-century mathematical and astronomical treatise on the apparent motions of the stars and planetary paths. Written in Greek by Claudius Ptolemy, a Roman era scholar of Egypt,...
, a treatise on mathematical astronomy. It is essentially equivalent to a table of values of the sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
function. It was the earliest trigonometric table extensive enough for many practical purposes, including those of astronomy (an earlier table of chords by Hipparchus
Hipparchus
Hipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour...
gave chords only for arcs that were multiples of 7½° = π/24 radians). Several centuries passed before more extensive trigonometric tables were created.
The chord function and the table
A chordChord (geometry)
A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
of a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
is a line segment whose endpoints are on the circle. Ptolemy considered a circle of diameter 120. He tabulated the length of a chord whose endpoints are separated by an arc of n degrees, for n ranging from 1/2 to 180 by increments of 1/2. In modern notation, the length of the chord corresponding to an arc of θ degrees is
As θ goes from 0 to 180, the chord of a θ° arc goes from 0 to 120. For tiny arcs, the chord is to the arc as π is to 3, or more precisely, the ratio can be made as close as desired to π/3 ≈ 1.04719755 by making θ small enough. Thus, for the arc of (1/2)°, the chord is slightly more than the arc. As the arc increases, the ratio of the chord to the arc decreases. When the arc reaches 60°, the chord is exactly equal to the arc, i.e. chord 60° = 60. For arcs of more than 60°, the chord is less than the arc, until an arc of 180° is reached, when the chord is only 120.
The fractional parts of chord lengths were expressed in sexagesimal, i.e. base-60, numerals. For example, where the length of a chord subtended by a 112° arc is reported to be "99 29 5", that means that its length is
rounded to the nearest 1/602.
After the columns for the arc and the chord, a third column is labeled "sixtieths". For an arc of θ°, the entry in the "sixtieths" column is
This is the average number of sixtieths that must be added to chord(θ°) for each 1° increase in θ°, between the entry for θ° and that for (θ + ½)°. Thus, it is used for linear interpolation
Linear interpolation
Linear interpolation is a method of curve fitting using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .-Linear interpolation between two known points:...
. Glowatzki and Göttsche showed that Ptolemy must have calculated chords to five sexigesimal places in order to achieve the degree of accuracy found in the "sixtieths" column.
-
How Ptolemy computed chords
Chapter 10 of Book I of the Almagest presents geometricEuclidean geometryEuclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
theorems used for computing chords. Ptolemy used geometric reasoning based on Proposition 10 of Book XIII of Euclid'sEuclidEuclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
ElementsEuclid's ElementsEuclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
to find the chords of 72° and 36°. That Proposition states that if an equilateral pentagonPentagonIn geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
is inscribed in a circle, then the area of the square on the side of the pentagon equals the sum of the areas of the squares on the sides of the hexagon and the decagonDecagonIn geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°...
inscribed in the same circle.
He used Ptolemy's theoremPtolemy's theoremIn Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral . The theorem is named after the Greek astronomer and mathematician Ptolemy...
on quadrilaterals inscribed in a circle to derive formulas for the chord of a half-arc, the chord of the sum of two arcs, and the chord of a difference of two arcs. The theorem states that for a quadrilateralQuadrilateralIn Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
inscribed in a circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, the product of the lengths of the diagonals equals the sum of the products of the two pairs of opposite sides. The derivations of trigonometric identities rely on a cyclic quadrilateralCyclic quadrilateralIn Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
in which one side is a diameter of the circle.
To find the chords of arcs of 1° and ½° he used approximations based on Aristarchus' inequalityAristarchus' inequalityIn trigonometry, Aristarchus' inequality, named after the ancient astronomer Aristarchus of Samos, states that if α and β are acute angles and β ...
. The inequality states that for arcs α and β with 0 < β < α < 90°, we have
Ptolemy showed that for arcs of 1° and ½°, when rounded to two sexigesimal places after the integer part, the approximations are accurate.
The numeral system and the appearance of the untranslated table
Lengths of arcs of the circle, in degrees, and the integer parts of chord lengths, were expressed in a base-10 numeral systemNumeral systemA numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
that used 21 letters of the Greek alphabet with the meanings given in the following table, and a symbol, "∠' ", that means 1/2. Two of the letters, labeled "archaic" below, had not been in use in the Greek language for some centuries before the Almagest was written.-
Thus, for example, an arc of ° is expressed as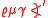
.
The fractional parts of chord lengths required great accuracy, and were given in two columns in the table: the first giving an integer multiple of 1/60, in the range 0–59, the second an integer multiple of 1/602 = 1/3600, also in the range 0–59.
Thus in Heiberg's edition of the Almagest with the table of chords on pages 48–63, the beginning of the table, corresponding to arcs from 1/2° through °, looks like this:-
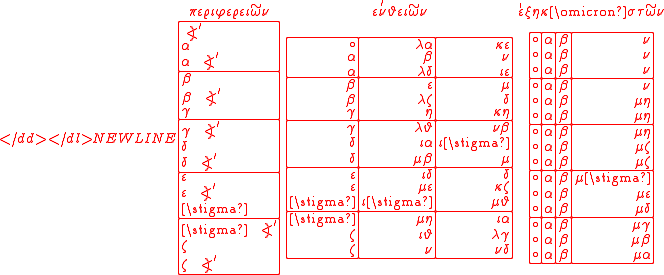
Later in the table, one can see the base-10 nature of the numerals expressing the integer parts of the arc and the chord length. Thus an arc of 85° is written as
(
for 80 and 
for 5) and not broken down into 60 + 25, and the corresponding chord length of 81 plus a fractional part begins with 
, likewise not broken into 60 + 21. But the fractional part, 4/60 + 15/602, is written as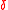 
, for 4, in the 1/60 column, followed by 
, for 15, in the 1/602 column.
-
The table has 45 lines on each of eight pages—thus 360 lines.
External links
- J. L. Heiberg'sJohan Ludvig Heiberg (historian)Johan Ludvig Heiberg was a Danish philologist and historian. He is best known for his discovery of previously unknown texts in the Archimedes Palimpsest, and for his edition of Euclid's Elements that T. L. Heath translated into English...
edition of the Almagest with the table of chords on pages 48–63 - Ptolemy's Table of Chords: Trigonometry in the Second Century, by Glenn Elert
- J. L. Heiberg's
-
-
-
