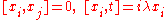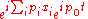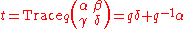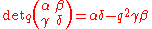Quantum spacetime
Encyclopedia
In mathematical physics, the concept of quantum spacetime is a generalization of the usual concept of spacetime
in which some variables that ordinarily commute
are assumed not to commute and form a different Lie algebra
. The choice of that algebra still varies from theory to theory.
As a result of this change some variables that are usually continuous may become discrete.
Often only such discrete variables are called ``quantized"; usage varies.
The idea of quantum spacetime was proposed in the early days of quantum theory by Heisenberg and Ivanenko
as a way to eliminate infinities from quantum field theory.
The germ of the idea passed from Heisenberg to Rudolf Peierls
, who noted that electrons in a magnetic field
can be regarded as moving in a quantum space-time, and to Robert Oppenheimer
, who carried it
to Hartland Snyder
,
who published the first concrete example .
Snyder's Lie algebra
was made simple by C. N Yang in the same year.
Physical reasons have been given to believe that physical spacetime is a quantum spacetime.
In quantum mechanics
position and momentum variables
are already noncommutative, obey the Heisenberg uncertainty principle, and are continuous.
Because of the Heisenberg uncertainty relations, greater energy is needed to probe smaller distances.
Ultimately, according to gravity theory, the probing particles form black holes and destroy what is to be measured. Then the process cannot be repeated, and so
does not count as a measurement.
This limited measurability led many to expect that our usual picture of continuous commutative spacetime breaks down at Planck scale
distances, if not sooner.
Again, physical spacetime is expected to be quantum because physical coordinates are already slightly noncommutative.
The astronomical coordinates of a star are modified by gravitational fields between us and the star, as in the deflection of light by the sun, one of the classic tests of general relativity
.
Therefore the coordinates actually depend on gravitational field variables.
According to quantum theories of gravity these field variables do not commute;
therefore coordinates that depend on them likely do not commute.
Both arguments are based on pure gravity and quantum theory, and they limit the measurement of time
by the only time constant in pure quantum gravity, the Planck time
.
Our instruments, however, are not purely gravitational but are made of particles. They may set a more severe, larger, limit than the Planck time.
Quantum spacetimes are often described mathematically using the noncommutative geometry
of Connes,
quantum geometry
, or quantum groups.
Any noncommutative algebra with at least four generators could be interpreted as a quantum spacetime, but
the following desiderata have been suggested:
This would permit wave equations for particles and fields and facilitate predictions for experimental deviations from classical spacetime physics that can then be tested experimentally.
Several models were found in the 1990s more or less meeting most of the above criteria.
for the spatial variables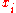
and the time variable 
. Here 
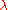has dimensions of time and is therefore expected to be something like the Planck time. The Poincaré group here is correspondingly deformed, now to a certain bicrossproduct quantum group with the following characteristic features.
The momentum generators
commute among themselves but addition of momenta, reflected in the quantum group structure, is deformed (momentum space becomes a non-abelian group). Meanwhile, the Lorentz group generators enjoy their usual relations among themselves but act non-linearly on the momentum space. The orbits for this action are depicted in the figure as a cross-section of 
against one of the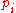 
. The on-shell region describing particles in the upper center of the image would normally be hyperboloids but these are now `squashed' into the cylinder
in simplified units. The upshot is that Lorentz-boosting a momentum will never increase it above the Planck momentum. The existence of a highest momentum scale or lowest distance scale fits the physical picture. This squashing comes from the non-linearity of the Lorentz boost and is an endemic feature of bicrossproduct quantum groups known since their introduction in 1988. Some physicists dub the bicrossproduct model doubly special relativity, since it sets an upper limit to both speed and momentum.
Another consequence of the squashing is that the propagation of particles is deformed, even of light, leading to a variable speed of light
. This prediction requires the particular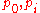
to be the physical energy and spatial momentum (as opposed to some other function of them). Arguments for this identification were provided in 1999 by Giovanni Amelino-Camelia
and Majid through a study of plane waves for a quantum differential calculus in the model. They take the form
in other words a form which is sufficiently close to classical that one might plausibly believe the interpretation. At the moment such wave analysis represents the best hope to obtain physically testable predictions form the model.
Prior to this work there were a number of unsupported claims to make predictions from the model based solely on the form of the Poincaré quantum group. There were also claims based on an earlier
-Poincaré quantum group introduced by Jurek Lukierski and co-workers which should be viewed as an important precursor to the bicrossproduct one, albeit without the actual quantum spacetime and with different proposed generators for which the above picture does not apply. The bicrossproduct model spacetime has also been called 
-deformed spacetime with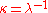 
.
in 1990 and by Majid and coworkers in a series of papers on braided matrices starting a year later. The point of view in the second approach is that usual Minkowski spacetime has a nice description via Pauli matrices
as the space of 2 x 2 hermitian matrices. In quantum group theory and using braided monoidal category methods one has a natural q-version of this defined here for real values of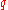
as a `braided hermitian matrix' of generators and relations
These relations say that the generators commute as
thereby recovering usual Minkowski space. One can work with more familiar variables 
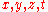as linear combinations of these. In particular, time
is given by a natural braided trace of the matrix and commutes with the other generators (so this model has a very different flavour from the bicrossproduct one). The braided-matrix picture also leads naturally to a quantity
which as
returns us the usual Minkowski distance (this translates to a metric in the quantum differential geometry). The parameter 
or 
is dimensionless and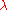 
is thought to be a ratio of the Planck scale and the cosmological length. That is, there are indications that that this model relates to quantum gravity with non-zero cosmological constant
, the choice of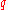
depending on whether this is positive or negative. We have described the mathematically better understood but perhaps less physically justified positive case here.
A full understanding of this model requires (and was concurrent with the development of) a full theory of `braided linear algebra' for such spaces. The momentum space for the theory is another copy of the same algebra and there is a certain `braided addition' of momentum on it expressed as the structure of a braided Hopf algebra
or quantum group in a certain braided monoidal category). This theory by 1993 had provided the corresponding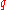
-deformed Poincaré group as generated by such translations and 
-Lorentz transformations, completing the interpretation as a quantum spacetime.
In the process it was discovered that the Poincaré group not only had to be deformed but had to be extended to include dilations of the quantum spacetime. For such a theory to be exact we would need all particles in the theory to be massless, which is consistent with experiment as masses of elementary particles are indeed vanishingly small compared to the Planck mass. If current thinking in cosmology is correct then this model is more appropriate, but it is significantly more complicated and for this reason its physical predictions have yet to be worked out.
algebra
familiar from quantum mechanics
but interpreted in this context as coordinates of a quantum space or spacetime. These relations were proposed by Roger Penrose
in his earliest spin network
theory of space. It is a toy model of quantum gravity in 3 spacetime dimensions (not the physical 4) with a Euclidean (not the physical Minkowskian) signature. It was again proposed in this context by Gerardus 't Hooft
. A further development including a quantum differential calculus and an action of a certain `quantum double' quantum group as deformed Euclidean group of motions was given by Majid and E. Batista
A striking feature of the noncommutative geometry here is that the smallest covariant quantum differential calculus has one dimension higher than expected, namely 4, suggesting that the above can also be viewed as the spatial part of a 4-dimensional quantum spacetime. The model should not be confused with fuzzy sphere
s which are finite-dimensional matrix algebras which one can think of as spheres in the spin model spacetime of fixed radius.
proposes that
where the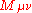
generate the Lorentz group. This quantum spacetime and that of C. N. Yang entail a radical unification of spacetime, energy-momentum, and angular momentum.
The idea was revived in a modern context by Sergio Doplicher, Claus Fredenhagen and John Roberts in 1995
by letting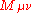
simply be viewed as some function of 
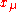as defined by the above relation, and any relations involving it viewed as higher order relations among the 
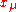. The Lorentz symmetry is arranged so as to transform the indices as usual and without being deformed.
An even simpler variant of this model is to let
here be a numerical antisymmetric tensor, in which context it is usually denoted 
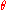, so the relations are 
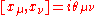. In even dimensions 
any nondegenerate such theta can be transformed to a normal form in which this really is just the Heisenberg algebra but the difference that the variables are being proposed as those of spacetime. This proposal was for a time quite popular because of its familiar form of relations and because it has been argued that it emerges from the theory of open strings landing on D-branes, see noncommutative quantum field theory
and Moyal plane. However, it should be realised that this D-brane lives in some of the higher spacetime dimensions in the theory and hence it is not our physical spacetime that string theory suggests to be effectively quantum in this way. You also have to subscribe to D-branes as an approach to quantum gravity in the first place. Even when posited as quantum spacetime it is hard to obtain physical predictions and one reason for this is that if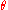
is a tensor then by dimensional analysis it should have dimensions of length
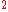, and if this length is speculated to be the Planck length then the effects would be even harder to ever detect than for other models.
and coworkers have argued that the coordinate algebra of this extra part should be replaced by a finite-dimensional noncommutative algebra. For a certain reasonable choice of this algebra, its representation and extended Dirac operator, one is able to recover the Standard Model
of elementary particles. In this point of view the different kinds of matter particles are manifestations of geometry in these extra noncommutative directions. Connes first works here date from 1989 but has been developed considerably since then. Such an approach can theoretically be combined with quantum spacetime as above.
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
in which some variables that ordinarily commute
Commute
Commute, commutation or commutative may refer to:* Commuting, the process of travelling between a place of residence and a place of work* Commutative property, a property of a mathematical operation...
are assumed not to commute and form a different Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
. The choice of that algebra still varies from theory to theory.
As a result of this change some variables that are usually continuous may become discrete.
Often only such discrete variables are called ``quantized"; usage varies.
The idea of quantum spacetime was proposed in the early days of quantum theory by Heisenberg and Ivanenko
as a way to eliminate infinities from quantum field theory.
The germ of the idea passed from Heisenberg to Rudolf Peierls
Rudolf Peierls
Sir Rudolf Ernst Peierls, CBE was a German-born British physicist. Rudolf Peierls had a major role in Britain's nuclear program, but he also had a role in many modern sciences...
, who noted that electrons in a magnetic field
can be regarded as moving in a quantum space-time, and to Robert Oppenheimer
Robert Oppenheimer
Julius Robert Oppenheimer was an American theoretical physicist and professor of physics at the University of California, Berkeley. Along with Enrico Fermi, he is often called the "father of the atomic bomb" for his role in the Manhattan Project, the World War II project that developed the first...
, who carried it
to Hartland Snyder
Hartland Snyder
Hartland Sweet Snyder was a physicist who along with Robert Oppenheimer calculated the gravitational collapse of a pressure-free homogenous fluid sphere, and found that it could not communicate with the rest of the universe....
,
who published the first concrete example .
Snyder's Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
was made simple by C. N Yang in the same year.
Physical reasons have been given to believe that physical spacetime is a quantum spacetime.
In quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
position and momentum variables
are already noncommutative, obey the Heisenberg uncertainty principle, and are continuous.Because of the Heisenberg uncertainty relations, greater energy is needed to probe smaller distances.
Ultimately, according to gravity theory, the probing particles form black holes and destroy what is to be measured. Then the process cannot be repeated, and so
does not count as a measurement.
This limited measurability led many to expect that our usual picture of continuous commutative spacetime breaks down at Planck scale
Planck scale
In particle physics and physical cosmology, the Planck scale is an energy scale around 1.22 × 1019 GeV at which quantum effects of gravity become strong...
distances, if not sooner.
Again, physical spacetime is expected to be quantum because physical coordinates are already slightly noncommutative.
The astronomical coordinates of a star are modified by gravitational fields between us and the star, as in the deflection of light by the sun, one of the classic tests of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
.
Therefore the coordinates actually depend on gravitational field variables.
According to quantum theories of gravity these field variables do not commute;
therefore coordinates that depend on them likely do not commute.
Both arguments are based on pure gravity and quantum theory, and they limit the measurement of time
by the only time constant in pure quantum gravity, the Planck time
Planck time
In physics, the Planck time, , is the unit of time in the system of natural units known as Planck units. It is the time required for light to travel, in a vacuum, a distance of 1 Planck length...
.
Our instruments, however, are not purely gravitational but are made of particles. They may set a more severe, larger, limit than the Planck time.
Quantum spacetimes are often described mathematically using the noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
of Connes,
quantum geometry
Quantum geometry
In theoretical physics, quantum geometry is the set of new mathematical concepts generalizing the concepts of geometry whose understanding is necessary to describe the physical phenomena at very short distance scales...
, or quantum groups.
Any noncommutative algebra with at least four generators could be interpreted as a quantum spacetime, but
the following desiderata have been suggested:
- Local Lorentz groupLorentz groupIn physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
and Poincaré groupPoincaré groupIn physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
symmetries should be retained, possibly in a generalised form. Their generalisation often takes the form of a quantum groupQuantum groupIn mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
acting on the quantum spacetime algebra.
- The algebra might plausibly arise in an effective description of quantum gravity effects in some regime of that theory. For example, a physical parameter
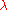, perhaps the Planck length, might control the deviation from commutative classical spacetime, so that ordinary Lorentzian spacetime arises as 
.
- There might be a notion of quantum differential calculusQuantum differential calculusIn quantum geometry or noncommutative geometry a quantum differential calculus or noncommtuative differential structure on an algebra A over a field k means the specification of a space of `differential forms' over the algebra...
on the quantum spacetime algebra, compatible with the (quantum) symmetry and preferably reducing to the usual differential calculus as
.
This would permit wave equations for particles and fields and facilitate predictions for experimental deviations from classical spacetime physics that can then be tested experimentally.
- The Lie algebra should be semisimpleSemisimpleIn mathematics, the term semisimple is used in a number of related ways, within different subjects. The common theme is the idea of a decomposition into 'simple' parts, that fit together in the cleanest way...
(Yang, I. E. Segal 1947). This makes it easier to formulate a finite theory.
Several models were found in the 1990s more or less meeting most of the above criteria.
Bicrossproduct model spacetime
The bicrossproduct model spacetime was introduced by Shahn Majid and Henri Ruegg and has Lie algebra relations
for the spatial variables
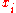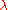and the time variable . Here has dimensions of time and is therefore expected to be something like the Planck time. The Poincaré group here is correspondingly deformed, now to a certain bicrossproduct quantum group with the following characteristic features.The momentum generators
commute among themselves but addition of momenta, reflected in the quantum group structure, is deformed (momentum space becomes a non-abelian group). Meanwhile, the Lorentz group generators enjoy their usual relations among themselves but act non-linearly on the momentum space. The orbits for this action are depicted in the figure as a cross-section of against one of the 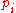. The on-shell region describing particles in the upper center of the image would normally be hyperboloids but these are now `squashed' into the cylinder
in simplified units. The upshot is that Lorentz-boosting a momentum will never increase it above the Planck momentum. The existence of a highest momentum scale or lowest distance scale fits the physical picture. This squashing comes from the non-linearity of the Lorentz boost and is an endemic feature of bicrossproduct quantum groups known since their introduction in 1988. Some physicists dub the bicrossproduct model doubly special relativity, since it sets an upper limit to both speed and momentum.
Another consequence of the squashing is that the propagation of particles is deformed, even of light, leading to a variable speed of light
Variable speed of light
The variable speed of light concept states that the speed of light in a vacuum, usually denoted by c, may not be constant in most cases. In most situations in condensed matter physics when light is traveling through a medium, it effectively has a slower speed...
. This prediction requires the particular
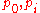to be the physical energy and spatial momentum (as opposed to some other function of them). Arguments for this identification were provided in 1999 by Giovanni Amelino-CameliaGiovanni Amelino-Camelia
Giovanni Amelino-Camelia is an Italian physicist of the University of Rome La Sapienza who works on quantum gravity.He is the first proposer of Doubly special relativity that is the idea of introducing the Planck length in physics as an observer-independent quantity, obtaining a relativistic theory...
and Majid through a study of plane waves for a quantum differential calculus in the model. They take the form
in other words a form which is sufficiently close to classical that one might plausibly believe the interpretation. At the moment such wave analysis represents the best hope to obtain physically testable predictions form the model.
Prior to this work there were a number of unsupported claims to make predictions from the model based solely on the form of the Poincaré quantum group. There were also claims based on an earlier
-Poincaré quantum group introduced by Jurek Lukierski and co-workers which should be viewed as an important precursor to the bicrossproduct one, albeit without the actual quantum spacetime and with different proposed generators for which the above picture does not apply. The bicrossproduct model spacetime has also been called -deformed spacetime with 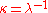.q-Deformed spacetime
This model was introduced independently by a team working under Julius WessJulius Wess
Julius Wess was an Austrian theoretical physicist noted as the co-inventor of the Wess–Zumino model and Wess–Zumino–Witten model in the field of supersymmetry...
in 1990 and by Majid and coworkers in a series of papers on braided matrices starting a year later. The point of view in the second approach is that usual Minkowski spacetime has a nice description via Pauli matrices
Pauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
as the space of 2 x 2 hermitian matrices. In quantum group theory and using braided monoidal category methods one has a natural q-version of this defined here for real values of
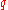as a `braided hermitian matrix' of generators and relations
These relations say that the generators commute as
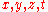thereby recovering usual Minkowski space. One can work with more familiar variables as linear combinations of these. In particular, time
is given by a natural braided trace of the matrix and commutes with the other generators (so this model has a very different flavour from the bicrossproduct one). The braided-matrix picture also leads naturally to a quantity
which as
returns us the usual Minkowski distance (this translates to a metric in the quantum differential geometry). The parameter or is dimensionless and 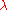is thought to be a ratio of the Planck scale and the cosmological length. That is, there are indications that that this model relates to quantum gravity with non-zero cosmological constantCosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
, the choice of
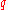depending on whether this is positive or negative. We have described the mathematically better understood but perhaps less physically justified positive case here.A full understanding of this model requires (and was concurrent with the development of) a full theory of `braided linear algebra' for such spaces. The momentum space for the theory is another copy of the same algebra and there is a certain `braided addition' of momentum on it expressed as the structure of a braided Hopf algebra
Braided Hopf algebra
In mathematics a braided Hopf algebra is a Hopf algebra in a braided monoidal category. The most common braided Hopf algebras are objects in a Yetter–Drinfel'd category of a Hopf algebra H, particurlarly the Nichols algebra of a braided vectorspace in that category.The notion should not be confused...
or quantum group in a certain braided monoidal category). This theory by 1993 had provided the corresponding
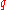-deformed Poincaré group as generated by such translations and -Lorentz transformations, completing the interpretation as a quantum spacetime.In the process it was discovered that the Poincaré group not only had to be deformed but had to be extended to include dilations of the quantum spacetime. For such a theory to be exact we would need all particles in the theory to be massless, which is consistent with experiment as masses of elementary particles are indeed vanishingly small compared to the Planck mass. If current thinking in cosmology is correct then this model is more appropriate, but it is significantly more complicated and for this reason its physical predictions have yet to be worked out.
Fuzzy or spin model spacetime
This refers in modern usage to the angular momentumAngular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
algebra
familiar from quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
but interpreted in this context as coordinates of a quantum space or spacetime. These relations were proposed by Roger Penrose
Roger Penrose
Sir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...
in his earliest spin network
Spin network
In physics, a spin network is a type of diagram which can be used to represent states and interactions between particles and fields in quantum mechanics. From a mathematical perspective, the diagrams are a concise way to represent multilinear functions and functions between representations of...
theory of space. It is a toy model of quantum gravity in 3 spacetime dimensions (not the physical 4) with a Euclidean (not the physical Minkowskian) signature. It was again proposed in this context by Gerardus 't Hooft
Gerardus 't Hooft
Gerardus 't Hooft is a Dutch theoretical physicist and professor at Utrecht University, the Netherlands. He shared the 1999 Nobel Prize in Physics with his thesis advisor Martinus J. G...
. A further development including a quantum differential calculus and an action of a certain `quantum double' quantum group as deformed Euclidean group of motions was given by Majid and E. Batista
A striking feature of the noncommutative geometry here is that the smallest covariant quantum differential calculus has one dimension higher than expected, namely 4, suggesting that the above can also be viewed as the spatial part of a 4-dimensional quantum spacetime. The model should not be confused with fuzzy sphere
Fuzzy sphere
In mathematics, the fuzzy sphere is one of the simplest and most canonical examples of non-commutative geometry. Ordinarily, the functions defined on a sphere form a commuting algebra. A fuzzy sphere differs from an ordinary sphere because the algebra of functions on it is not commutative. It is...
s which are finite-dimensional matrix algebras which one can think of as spheres in the spin model spacetime of fixed radius.
Heisenberg model spacetimes
The quantum spacetime of Hartland SnyderHartland Snyder
Hartland Sweet Snyder was a physicist who along with Robert Oppenheimer calculated the gravitational collapse of a pressure-free homogenous fluid sphere, and found that it could not communicate with the rest of the universe....
proposes that
where the
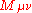generate the Lorentz group. This quantum spacetime and that of C. N. Yang entail a radical unification of spacetime, energy-momentum, and angular momentum.The idea was revived in a modern context by Sergio Doplicher, Claus Fredenhagen and John Roberts in 1995
by letting
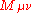simply be viewed as some function of 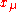as defined by the above relation, and any relations involving it viewed as higher order relations among the 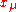. The Lorentz symmetry is arranged so as to transform the indices as usual and without being deformed.An even simpler variant of this model is to let
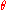here be a numerical antisymmetric tensor, in which context it is usually denoted , so the relations are 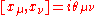. In even dimensions any nondegenerate such theta can be transformed to a normal form in which this really is just the Heisenberg algebra but the difference that the variables are being proposed as those of spacetime. This proposal was for a time quite popular because of its familiar form of relations and because it has been argued that it emerges from the theory of open strings landing on D-branes, see noncommutative quantum field theoryNoncommutative quantum field theory
In mathematical physics, noncommutative quantum field theory is an application of noncommutative mathematics to the spacetime of quantum field theory that is an outgrowth of noncommutative geometry and index theory in which the coordinate functions are noncommutative...
and Moyal plane. However, it should be realised that this D-brane lives in some of the higher spacetime dimensions in the theory and hence it is not our physical spacetime that string theory suggests to be effectively quantum in this way. You also have to subscribe to D-branes as an approach to quantum gravity in the first place. Even when posited as quantum spacetime it is hard to obtain physical predictions and one reason for this is that if
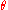is a tensor then by dimensional analysis it should have dimensions of length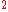, and if this length is speculated to be the Planck length then the effects would be even harder to ever detect than for other models.Noncommutative extensions to spacetime
Although not quantum spacetime in the sense above, another use of noncommutative geometry is to tack on `noncommutative extra dimensions' at each point of ordinary spacetime. Instead of invisible curled up extra dimensions as in string theory, Alain ConnesAlain Connes
Alain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
and coworkers have argued that the coordinate algebra of this extra part should be replaced by a finite-dimensional noncommutative algebra. For a certain reasonable choice of this algebra, its representation and extended Dirac operator, one is able to recover the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of elementary particles. In this point of view the different kinds of matter particles are manifestations of geometry in these extra noncommutative directions. Connes first works here date from 1989 but has been developed considerably since then. Such an approach can theoretically be combined with quantum spacetime as above.
See also
- Quantum groupQuantum groupIn mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
- Quantum geometryQuantum geometryIn theoretical physics, quantum geometry is the set of new mathematical concepts generalizing the concepts of geometry whose understanding is necessary to describe the physical phenomena at very short distance scales...
- Noncommutative geometryNoncommutative geometryNoncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
- Quantum gravityQuantum gravityQuantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
- Anabelian topologyAnabelian geometryAnabelian geometry is a proposed theory in mathematics, describing the way the algebraic fundamental group G of an algebraic variety V, or some related geometric object, determines how V can be mapped into another geometric object W, under the assumption that G is very far from being an abelian...
Further reading
- R. P. Grimaldi, Discrete and Combinatorial Mathematics: An Applied Introduction, 4th Ed. Addison-Wesley 1999.
- J. Matousek, J. Nesetril, Invitation to Discrete Mathematics. Oxford University Press 1998.
- Taylor E. F., John A. Wheeler, Spacetime Physics, publisher W. H. Freeman, 1963.
External links
- Plus Magazine article on quantum geometry by Marianne Freiberger