Quasi-set theory
Encyclopedia
Quasi-set theory is a formal mathematical theory for dealing with collections of indistinguishable objects, mainly motivated by the assumption that certain objects treated in quantum physics are indistinguishable and don't have individuality.
Hilbert
proposed in 1900. An outcome of that meeting was a new list of mathematical problems, the first of which, due to Manin (1976, p. 36), questioned whether classical set theory
was an adequate paradigm for treating collections of indistinguishable elementary particle
s in quantum mechanics
. He suggested that such collections cannot be sets in the usual sense, and that the study of such collections required a "new language".
The use of the term quasi-set follows a suggestion in da Costa's 1980 monograph Ensaio sobre os Fundamentos da Lógica (see da Costa and Krause 1994), in which he explored possible semantics
for what he called "Schrödinger Logics". In these logics, the concept of identity is restricted to some objects of the domain, and has motivation in Schrödinger's claim that the concept of identity does not make sense for elementary particles (Schrödinger 1952). Thus in order to provide a semantics that fits the logic, da Costa submitted that "a theory of quasi-sets should be developed", encompassing "standard sets" as particular cases, yet da Costa did not develop this theory in any concrete way. To the same end and independently of da Costa, Dalla Chiara and di Francia (1993) proposed a theory of quasets to enable a semantic
treatment of the language of microphysics. The first quasi-set theory was proposed by D. Krause in his PhD thesis, in 1990 (see Krause 1992).
On the use of quasi-sets in philosophical discussions of quantum identity and individuality, see French (2006) and French and Krause (2006). On Schrödinger logics, see da Costa and Krause (1994, 1997), and French and Krause (2006).
, the first quasi-set theory; other formulations and improvements have since appeared. For an updated paper on the subject, see French and Krause (2010). Krause builds on the set theory ZFU, consisting of Zermelo-Fraenkel set theory with an ontology
extended to include two kinds of urelements:
Quasi-sets (q-sets) are collections resulting from applying axioms, very similar to those for ZFU, to a basic domain composed of m-atoms, M-atoms, and aggregates of these. The axioms of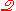
include equivalents of extensionality
, but in a weaker form, termed "weak extensionality axiom"; axioms asserting the existence of the empty set
, unordered pair
, union set
, and power set
; Separation; the image of a q-set under a q-function is also a q-set; q-set equivalents of Infinity
, Regularity
, and Choice. Q-set theories based on other set-theoretical frameworks are, of course, possible.
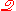has a primitive concept of quasi-cardinal, governed by eight additional axioms, intuitively standing for the quantity of objects in a collection. The quasi-cardinal of a quasi-set is not defined in the usual sense (by means of ordinals
) because the m-atoms are assumed (absolutely) indistinguishable. Furthermore, it is possible to define a translation from the language of ZFU into the language of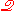
in such a way so that there is a 'copy' of ZFU in 
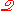. In this copy, all the usual mathematical concepts can be defined, and the 'sets' (in reality, the '
-sets') turn out to be those q-sets whose transitive closure
contains no m-atoms.
In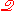
there may exist q-sets, called "pure" q-sets, whose elements are all m-atoms, and the axiomatics of 
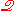provides the grounds for saying that nothing in 
distinguishes the elements of a pure q-set from one another, for certain pure q-sets. Within the theory, the idea that there is more than one entity in x is expressed by an axiom which states that the quasi-cardinal of the power quasi-set of x has quasi-cardinal 2qc(x), where qc(x) is the quasi-cardinal of x (which is a cardinal obtained in the 'copy' of ZFU just mentioned).
What exactly does this mean? Consider the level 2p of a sodium atom, in which there are six indiscernible electrons. Even so, physicists reason as if there are in fact six entities in that level, and not only one. In this way, by saying that the quasi-cardinal of the power quasi-set of x is 2qc(x) (suppose that qc(x) = 6 to follow the example), we are not excluding the hypothesis that there can exist six subquasi-sets of x which are 'singletons', although we cannot distinguish among them. Whether there are or not six elements in x is something which cannot be ascribed by the theory (although the notion is compatible with the theory). If the theory could answer this question, the elements of x would be individualized and hence counted, contradicting the basic assumption that they cannot be distinguished.
In other words, we may consistently (within the axiomatics of
) reason as if there are six entities in x, but x must be regarded as a collection whose elements cannot be discerned as individuals. Using quasi-set theory, we can express some facts of quantum physics without introducing symmetry
conditions (Krause et al. 1999, 2005). As is well known, in order to express indistinguishability, the particles are deemed to be individuals, say by attaching them to coordinates or to adequate functions/vectors like |ψ>. Thus, given two quantum systems labeled |ψ1> and |ψ2> at the outset, we need to consider a function like |ψ12> = |ψ1>|ψ2> ± |ψ2>|ψ1> (except for certain constants), which keep the quanta indistinguishable by permutation
s; the probability density
of the joint system independs on which is quanta #1 and which is quanta #2. (Note that precision requires that we talk of "two" quanta without distinguishing them, which is impossible in conventional set theories.) In
, we can dispense with this "identification" of the quanta
; for details, see Krause et al. (1999, 2005) and French and Krause (2006).
Quasi-set theory is a way to operationalize Heinz Post's (1963) claim that quanta should be deemed indistinguishable "right from the start."
of them may be indistinguishable without turning out to be
identical. Of course this is not a strict `definition' of a
quasi-set, but act more or less as Cantor's `definition' of a set
as ``any collection into a whole "M" of definite and separate,
that is, distinguishable objects "m" of our intuition or our
thought" serving just to provide an intuitive account of the
concept. For detail we recommend the discussion in (French and Krause
2006).
The quasi-set theory, that have been denoted by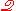
has in its main motivations some considerations taken from quantum
physics, mainly in considering Schr\"odinger's idea that the
concept of identity do not make sense when applied to elementary
particles (Schr\"odinger 1952, pp.17-18). In his words, he
considered just non-relativistic quantum mechanics. Another
motivation is, in our opinion, the need, stemming from
philosophical worries, of dealing with collections of absolutely
indistinguishable items that not need be the same
ones. (This is of course a way of speech.) Of course,
viewed from a formal point of view, ,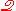
can also be
developed independently of any intended interpretation, but here
we shall always keep in mind this `quantum' motivation since,
after all, it is the intended interpretation that has originated
the problem of the development of the theory.
The first point is to guarantee that identity and
indistinguishability (or indiscernibility) will not collapse into
one another when the theory is formally developed. We assume that
identity, that will be symbolized by `=', is not a primitive
relation, but the theory has a weaker concept of
indistinguishability, symbolized by `
', instead. This is
just an equivalence relation and holds among all objects of the
considered domain. If the domain is divided up into objects of two
kinds, the "m"-objects, that standing for `micro-objects', and
"M"-objects, for `macro-objects', and quasi-sets of them (probably
having other quasi-sets as elements as well), then the identity
(defined with all the properties of standard identity of ZF) can
be defined for "M"-objects and quasi-sets having no "m"-objects in
their transitive closure. Thus, if we take just the part of theory
obtained by ruling out the "m"-objects and collections
(quasi-sets) whose have "m"-objects in their transitive closure,
we obtain a copy of ZFU (ZF with Urelemente); if we further
eliminate the "M"-objects, we get just a copy of the `pure' ZF.
Technically, expressions like "x = y" are not always well formed,
because they are not formulas when either "x" or "y" denote
"m"-objects. We express that by saying that the concept of
identity does not make sense for all objects. One time else, it
should be understood that this is just a way of speech. The
$m$-objects to which the defined concept of identity does not
apply are termed non individual by historical reasons (French and
Krause, 2006). As a result from the axioms of the theory
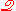, we can form collections of "m"-objects which have
no identity—in this sense; these collections may have a cardinal
(termed its `quasi-cardinal') but not an associated ordinal. Thus,
the concepts of ordinal and cardinal are independent, as in some
formulations of ZF proper. So, informally speaking, a quasi-set of
$m$-objects is such that its elements cannot be identified by
names, counted, ordered, although there is a sense in saying that
these collections have a cardinal which cannot be defined from
ordinals.
It is important to remark that, when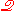
is used in
connection with quantum physics, the "m"-objects are thought of as
representing quantum entities (henceforth q-objects), but they are
not necessarily `particles' in the standard sense. Generally
speaking, whatever `objects' sharing the property of being
indistinguishable can also be values of the variables of
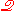. For a survey of the various different meanings
that the word `particle' has acquired in connection with quantum
physics see (Falkenburg 2007).
Another important feature of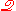
is that standard
mathematics can be developed using its resources, because the
theory is conceived in such a way that ZFU (and hence also ZF,
perhaps with the axiom of choice, ZFC) is a subtheory of
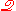. In other words, the theory is constructed so that
it extends standard Zermelo-Fraenkel with "Urelemente"
(ZFU); thus standard sets of ZFU must be viewed as particular
qsets, that is, there are qsets that have all the properties of
the sets of ZFU, and the objects of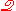
that
corresponds to the "Urelemente" of ZFU are identified with
the "M"-atoms of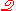
). The `sets' in 
will be called "q"-sets, or just "sets" for short. To make
the distinction, the language of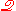
encompasses a
unary predicate "Z" such that "Z(x)" says that "x" is a set. It is
also possible to show that there is a translation from the
language of ZFU into the language of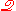
, so that the
translations of the postulates of ZFU are theorems of
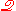; thus, there is a `copy' of ZFU in 
,
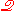and we refer to it as the `classical' part of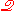
. In
this copy, all the usual mathematical concepts can be stated, as
for instance, the concept of ordinal (for the "q"-sets). This
`classical part' of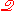
plays an important role in the
formal developments of the next sections.
Furthermore, it should be recalled that the theory is constructed
so that the relation of indiscernibility, when applied to
"M"-atoms or "M"-sets, collapses into standard identity of ZFU.
The "q"-sets are qsets whose transitive closure, as usually
defined, does not contain "m"-atoms or, in other words, they are
constructed in the "classical" part of the theory.
In order to distinguish between "Z"-sets and qsets that may have
"m"-atoms in their transitive closure, we write (in the
metalanguage)
for the former and 
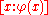for the latter. In 
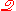, we term `pure'
those qsets that have only "m"-objects as elements (although these
elements may be not always indistinguishable from one another,
that is, the theory is consistent with the assumption of the
existence of different kinds of "m"-atoms—that is, not all of
them must be indiscernible from one another), and to them it is
assumed that the usual notion of identity cannot be applied (that
is, let us recall, "x = y", as well as its negation,
,
are not well formed formulas if either "x" or "y" stand for
"m"-objects). Notwithstanding, the primitive relation
applies to them, and it has the properties of an equivalence
relation.
The concept of ' extensional identity' , as said above, is a
defined notion, and it has the properties of standard identity of
ZFU. More precisely, we write
(read ' "x" and "y" are
extensionally identical') iff they are both qsets having the same
elements (that is,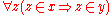
) or
they are both "M"-atoms and belong to the same qsets (that is,
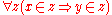). From now on, we shall
not bother to always write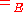
, using simply the symbol "=
for the extensional equality, as we have done above.
Since "m"-atoms are to stand for entities which cannot be labeled,
for they do not enter in the relation of identity, it is not
possible in general to attribute an ordinal to collections whose
elements are denoted by "m"-atoms. As a consequence, for these
collections it is not possible to define the notion of cardinal
number in the usual way, that is, through ordinals. (We just recall that an ordinal is a transitive set which
is well-ordered by the membership relation, and that a cardinal is
an ordinal
such that for no 
there does
not exist a bijection from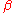
to 
. In the version of the theory we
shall be considering, to remedy this situation, we admit also a
primitive concept of quasi-cardinal which intuitively stands for
the `quantity' of objects in a collection.(The notion of
quasi-cardinal can be defined for finite quasi-sets; see Domenech
and Holik 2007.) The axioms for this notion grant that certain
quasi-sets "x" (in particular, those whose elements are
"m"-objects) may have a quasi-cardinal, written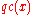
, even when
it is not possible to attribute an ordinal to them.
To link the relation of indistinguishability with qsets, the
theory also encompasses an `axiom of weak extensionality', which
states (informally speaking) that those quasi-sets that have the
same quantity (expressed by means of quasi-cardinals) of elements
of the same sort (in the sense that they belong to the same
equivalence class of indistinguishable objects) are
indistinguishable by their own. One of the interesting
consequences of this axiom is related to the quasi-set version of
the non observability of permutations, which is one of the most
basic facts regarding indistinguishable quanta (for a discussion
on this point, see French and Rickles 2003). In brief, remember
that in standard set theories, if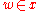
, then of course 
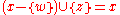iff 
. That is, we can 'exchange'
(without modifying the original arrangement) two elements iff they
are \textit{the same} elements, by force of the axiom of
extensionality. In contrast, in
we can prove the
following theorem, where
(and similarly 
) stand for
a quasi-set with quasi-cardinal 1 whose only element is
indistinguishable from "z" (respectively, from "w") --the reader
shouldn't think that this element "is identical to either"
"z" or "w", for the relation of equality doesn't apply to these
items; the set theoretical operations can be understood according
to their usual definitions):
Theorem: (Unobservability of
Permutations) Let "x" be a finite quasi-set such that
"x" does not contain all indistinguishable from "z", where "z" is
an "m"-atom such that
. If 
and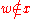 
,
then there exists
such that 
The theorem works to the effect that, supposing that "x" has "n"
elements, then if we `exchange' their elements "z" by
corresponding indistinguishable elements "w" (set theoretically,
this means performing the operation
),
then the resulting quasi-set remains \textit{indistinguishable}
from the one we started with. In a certain sense, it does not
matter whether we are dealing with "x" or with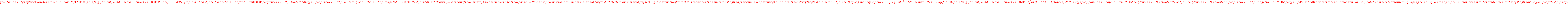
. So, within 
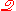, we can express that
`permutations are not observable', without necessarily introducing
symmetry postulates, and in particular to derive `in a natural
way' the quantum statistics (see French and
Krause 2006, chap.7). Further applications to the foundations of
quantum mechanics can be seen in Domenech et al. 2008.
Motivation
The American Mathematical Society sponsored a 1974 meeting to evaluate the resolution and consequences of the 23 problemsHilbert's problems
Hilbert's problems form a list of twenty-three problems in mathematics published by German mathematician David Hilbert in 1900. The problems were all unsolved at the time, and several of them were very influential for 20th century mathematics...
Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
proposed in 1900. An outcome of that meeting was a new list of mathematical problems, the first of which, due to Manin (1976, p. 36), questioned whether classical set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
was an adequate paradigm for treating collections of indistinguishable elementary particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
s in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. He suggested that such collections cannot be sets in the usual sense, and that the study of such collections required a "new language".
The use of the term quasi-set follows a suggestion in da Costa's 1980 monograph Ensaio sobre os Fundamentos da Lógica (see da Costa and Krause 1994), in which he explored possible semantics
Semantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
for what he called "Schrödinger Logics". In these logics, the concept of identity is restricted to some objects of the domain, and has motivation in Schrödinger's claim that the concept of identity does not make sense for elementary particles (Schrödinger 1952). Thus in order to provide a semantics that fits the logic, da Costa submitted that "a theory of quasi-sets should be developed", encompassing "standard sets" as particular cases, yet da Costa did not develop this theory in any concrete way. To the same end and independently of da Costa, Dalla Chiara and di Francia (1993) proposed a theory of quasets to enable a semantic
Semantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
treatment of the language of microphysics. The first quasi-set theory was proposed by D. Krause in his PhD thesis, in 1990 (see Krause 1992).
On the use of quasi-sets in philosophical discussions of quantum identity and individuality, see French (2006) and French and Krause (2006). On Schrödinger logics, see da Costa and Krause (1994, 1997), and French and Krause (2006).
Outline of the theory
We now expose Krause's (1992) axiomatic theory, the first quasi-set theory; other formulations and improvements have since appeared. For an updated paper on the subject, see French and Krause (2010). Krause builds on the set theory ZFU, consisting of Zermelo-Fraenkel set theory with an ontologyOntology
Ontology is the philosophical study of the nature of being, existence or reality as such, as well as the basic categories of being and their relations...
extended to include two kinds of urelements:
- m-atoms, whose intended interpretation is elementary quantum particles;
- M-atoms, macroscopic objects to which classical logicClassical logicClassical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
is assumed to apply.
Quasi-sets (q-sets) are collections resulting from applying axioms, very similar to those for ZFU, to a basic domain composed of m-atoms, M-atoms, and aggregates of these. The axioms of
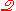include equivalents of extensionalityAxiom of extensionality
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
, but in a weaker form, termed "weak extensionality axiom"; axioms asserting the existence of the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, unordered pair
Axiom of pairing
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of pairing is one of the axioms of Zermelo–Fraenkel set theory.- Formal statement :...
, union set
Axiom of union
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of union is one of the axioms of Zermelo-Fraenkel set theory, stating that, for any set x there is a set y whose elements are precisely the elements of the elements of x...
, and power set
Axiom of power set
In mathematics, the axiom of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory.In the formal language of the Zermelo–Fraenkel axioms, the axiom reads:...
; Separation; the image of a q-set under a q-function is also a q-set; q-set equivalents of Infinity
Axiom of infinity
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
, Regularity
Axiom of regularity
In mathematics, the axiom of regularity is one of the axioms of Zermelo-Fraenkel set theory and was introduced by...
, and Choice. Q-set theories based on other set-theoretical frameworks are, of course, possible.
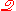has a primitive concept of quasi-cardinal, governed by eight additional axioms, intuitively standing for the quantity of objects in a collection. The quasi-cardinal of a quasi-set is not defined in the usual sense (by means of ordinalsOrdinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
) because the m-atoms are assumed (absolutely) indistinguishable. Furthermore, it is possible to define a translation from the language of ZFU into the language of
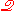in such a way so that there is a 'copy' of ZFU in 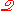. In this copy, all the usual mathematical concepts can be defined, and the 'sets' (in reality, the '-sets') turn out to be those q-sets whose transitive closureTransitive set
In set theory, a set A is transitive, if* whenever x ∈ A, and y ∈ x, then y ∈ A, or, equivalently,* whenever x ∈ A, and x is not an urelement, then x is a subset of A....
contains no m-atoms.
In
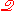there may exist q-sets, called "pure" q-sets, whose elements are all m-atoms, and the axiomatics of 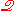provides the grounds for saying that nothing in distinguishes the elements of a pure q-set from one another, for certain pure q-sets. Within the theory, the idea that there is more than one entity in x is expressed by an axiom which states that the quasi-cardinal of the power quasi-set of x has quasi-cardinal 2qc(x), where qc(x) is the quasi-cardinal of x (which is a cardinal obtained in the 'copy' of ZFU just mentioned).What exactly does this mean? Consider the level 2p of a sodium atom, in which there are six indiscernible electrons. Even so, physicists reason as if there are in fact six entities in that level, and not only one. In this way, by saying that the quasi-cardinal of the power quasi-set of x is 2qc(x) (suppose that qc(x) = 6 to follow the example), we are not excluding the hypothesis that there can exist six subquasi-sets of x which are 'singletons', although we cannot distinguish among them. Whether there are or not six elements in x is something which cannot be ascribed by the theory (although the notion is compatible with the theory). If the theory could answer this question, the elements of x would be individualized and hence counted, contradicting the basic assumption that they cannot be distinguished.
In other words, we may consistently (within the axiomatics of
) reason as if there are six entities in x, but x must be regarded as a collection whose elements cannot be discerned as individuals. Using quasi-set theory, we can express some facts of quantum physics without introducing symmetrySymmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
conditions (Krause et al. 1999, 2005). As is well known, in order to express indistinguishability, the particles are deemed to be individuals, say by attaching them to coordinates or to adequate functions/vectors like |ψ>. Thus, given two quantum systems labeled |ψ1> and |ψ2> at the outset, we need to consider a function like |ψ12> = |ψ1>|ψ2> ± |ψ2>|ψ1> (except for certain constants), which keep the quanta indistinguishable by permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s; the probability density
Probability density
Probability density may refer to:* Probability density function in probability theory* The product of the probability amplitude with its complex conjugate in quantum mechanics...
of the joint system independs on which is quanta #1 and which is quanta #2. (Note that precision requires that we talk of "two" quanta without distinguishing them, which is impossible in conventional set theories.) In
, we can dispense with this "identification" of the quantaQuantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
; for details, see Krause et al. (1999, 2005) and French and Krause (2006).
Quasi-set theory is a way to operationalize Heinz Post's (1963) claim that quanta should be deemed indistinguishable "right from the start."
Some further details
Intuitively, a quasi-set is a collection of objects such that someof them may be indistinguishable without turning out to be
identical. Of course this is not a strict `definition' of a
quasi-set, but act more or less as Cantor's `definition' of a set
as ``any collection into a whole "M" of definite and separate,
that is, distinguishable objects "m" of our intuition or our
thought" serving just to provide an intuitive account of the
concept. For detail we recommend the discussion in (French and Krause
2006).
The quasi-set theory, that have been denoted by
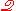
has in its main motivations some considerations taken from quantum
physics, mainly in considering Schr\"odinger's idea that the
concept of identity do not make sense when applied to elementary
particles (Schr\"odinger 1952, pp.17-18). In his words, he
considered just non-relativistic quantum mechanics. Another
motivation is, in our opinion, the need, stemming from
philosophical worries, of dealing with collections of absolutely
indistinguishable items that not need be the same
ones. (This is of course a way of speech.) Of course,
viewed from a formal point of view, ,
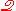can also bedeveloped independently of any intended interpretation, but here
we shall always keep in mind this `quantum' motivation since,
after all, it is the intended interpretation that has originated
the problem of the development of the theory.
The first point is to guarantee that identity and
indistinguishability (or indiscernibility) will not collapse into
one another when the theory is formally developed. We assume that
identity, that will be symbolized by `=', is not a primitive
relation, but the theory has a weaker concept of
indistinguishability, symbolized by `
', instead. This isjust an equivalence relation and holds among all objects of the
considered domain. If the domain is divided up into objects of two
kinds, the "m"-objects, that standing for `micro-objects', and
"M"-objects, for `macro-objects', and quasi-sets of them (probably
having other quasi-sets as elements as well), then the identity
(defined with all the properties of standard identity of ZF) can
be defined for "M"-objects and quasi-sets having no "m"-objects in
their transitive closure. Thus, if we take just the part of theory
obtained by ruling out the "m"-objects and collections
(quasi-sets) whose have "m"-objects in their transitive closure,
we obtain a copy of ZFU (ZF with Urelemente); if we further
eliminate the "M"-objects, we get just a copy of the `pure' ZF.
Technically, expressions like "x = y" are not always well formed,
because they are not formulas when either "x" or "y" denote
"m"-objects. We express that by saying that the concept of
identity does not make sense for all objects. One time else, it
should be understood that this is just a way of speech. The
$m$-objects to which the defined concept of identity does not
apply are termed non individual by historical reasons (French and
Krause, 2006). As a result from the axioms of the theory
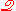, we can form collections of "m"-objects which haveno identity—in this sense; these collections may have a cardinal
(termed its `quasi-cardinal') but not an associated ordinal. Thus,
the concepts of ordinal and cardinal are independent, as in some
formulations of ZF proper. So, informally speaking, a quasi-set of
$m$-objects is such that its elements cannot be identified by
names, counted, ordered, although there is a sense in saying that
these collections have a cardinal which cannot be defined from
ordinals.
It is important to remark that, when
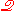is used inconnection with quantum physics, the "m"-objects are thought of as
representing quantum entities (henceforth q-objects), but they are
not necessarily `particles' in the standard sense. Generally
speaking, whatever `objects' sharing the property of being
indistinguishable can also be values of the variables of
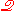. For a survey of the various different meaningsthat the word `particle' has acquired in connection with quantum
physics see (Falkenburg 2007).
Another important feature of
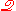is that standardmathematics can be developed using its resources, because the
theory is conceived in such a way that ZFU (and hence also ZF,
perhaps with the axiom of choice, ZFC) is a subtheory of
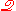. In other words, the theory is constructed so thatit extends standard Zermelo-Fraenkel with "Urelemente"
(ZFU); thus standard sets of ZFU must be viewed as particular
qsets, that is, there are qsets that have all the properties of
the sets of ZFU, and the objects of
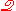thatcorresponds to the "Urelemente" of ZFU are identified with
the "M"-atoms of
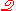). The `sets' in will be called "q"-sets, or just "sets" for short. To make
the distinction, the language of
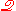encompasses aunary predicate "Z" such that "Z(x)" says that "x" is a set. It is
also possible to show that there is a translation from the
language of ZFU into the language of
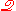, so that thetranslations of the postulates of ZFU are theorems of
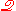; thus, there is a `copy' of ZFU in 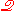,and we refer to it as the `classical' part of
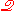. Inthis copy, all the usual mathematical concepts can be stated, as
for instance, the concept of ordinal (for the "q"-sets). This
`classical part' of
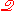plays an important role in theformal developments of the next sections.
Furthermore, it should be recalled that the theory is constructed
so that the relation of indiscernibility, when applied to
"M"-atoms or "M"-sets, collapses into standard identity of ZFU.
The "q"-sets are qsets whose transitive closure, as usually
defined, does not contain "m"-atoms or, in other words, they are
constructed in the "classical" part of the theory.
In order to distinguish between "Z"-sets and qsets that may have
"m"-atoms in their transitive closure, we write (in the
metalanguage)
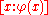for the former and for the latter. In 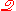, we term `pure'those qsets that have only "m"-objects as elements (although these
elements may be not always indistinguishable from one another,
that is, the theory is consistent with the assumption of the
existence of different kinds of "m"-atoms—that is, not all of
them must be indiscernible from one another), and to them it is
assumed that the usual notion of identity cannot be applied (that
is, let us recall, "x = y", as well as its negation,
,are not well formed formulas if either "x" or "y" stand for
"m"-objects). Notwithstanding, the primitive relation
applies to them, and it has the properties of an equivalence
relation.
The concept of ' extensional identity' , as said above, is a
defined notion, and it has the properties of standard identity of
ZFU. More precisely, we write
(read ' "x" and "y" areextensionally identical') iff they are both qsets having the same
elements (that is,
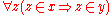) orthey are both "M"-atoms and belong to the same qsets (that is,
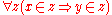). From now on, we shallnot bother to always write
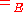, using simply the symbol "=for the extensional equality, as we have done above.
Since "m"-atoms are to stand for entities which cannot be labeled,
for they do not enter in the relation of identity, it is not
possible in general to attribute an ordinal to collections whose
elements are denoted by "m"-atoms. As a consequence, for these
collections it is not possible to define the notion of cardinal
number in the usual way, that is, through ordinals. (We just recall that an ordinal is a transitive set which
is well-ordered by the membership relation, and that a cardinal is
an ordinal
such that for no there doesnot exist a bijection from
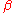to . In the version of the theory weshall be considering, to remedy this situation, we admit also a
primitive concept of quasi-cardinal which intuitively stands for
the `quantity' of objects in a collection.(The notion of
quasi-cardinal can be defined for finite quasi-sets; see Domenech
and Holik 2007.) The axioms for this notion grant that certain
quasi-sets "x" (in particular, those whose elements are
"m"-objects) may have a quasi-cardinal, written
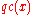, even whenit is not possible to attribute an ordinal to them.
To link the relation of indistinguishability with qsets, the
theory also encompasses an `axiom of weak extensionality', which
states (informally speaking) that those quasi-sets that have the
same quantity (expressed by means of quasi-cardinals) of elements
of the same sort (in the sense that they belong to the same
equivalence class of indistinguishable objects) are
indistinguishable by their own. One of the interesting
consequences of this axiom is related to the quasi-set version of
the non observability of permutations, which is one of the most
basic facts regarding indistinguishable quanta (for a discussion
on this point, see French and Rickles 2003). In brief, remember
that in standard set theories, if
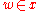, then of course 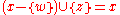iff . That is, we can 'exchange'(without modifying the original arrangement) two elements iff they
are \textit{the same} elements, by force of the axiom of
extensionality. In contrast, in
we can prove thefollowing theorem, where
(and similarly ) stand fora quasi-set with quasi-cardinal 1 whose only element is
indistinguishable from "z" (respectively, from "w") --the reader
shouldn't think that this element "is identical to either"
"z" or "w", for the relation of equality doesn't apply to these
items; the set theoretical operations can be understood according
to their usual definitions):
Theorem: (Unobservability of
Permutations) Let "x" be a finite quasi-set such that
"x" does not contain all indistinguishable from "z", where "z" is
an "m"-atom such that
. If and ,then there exists
such that The theorem works to the effect that, supposing that "x" has "n"
elements, then if we `exchange' their elements "z" by
corresponding indistinguishable elements "w" (set theoretically,
this means performing the operation
),then the resulting quasi-set remains \textit{indistinguishable}
from the one we started with. In a certain sense, it does not
matter whether we are dealing with "x" or with
. So, within , we can express that`permutations are not observable', without necessarily introducing
symmetry postulates, and in particular to derive `in a natural
way' the quantum statistics (see French and
Krause 2006, chap.7). Further applications to the foundations of
quantum mechanics can be seen in Domenech et al. 2008.